Fungsi pembolehubah sebenar dan perwakilan grafiknya

A fungsi pembolehubah sebenar Ambil nombor milik set nombor sebenar dan mengaitkannya dengan nilai lain, juga nyata, melalui peraturan surat -menyurat yang unik. Ini bermakna nombor sebenar diperoleh, melalui peraturan ini, imej yang unik.

Pembolehubah berlepas berangka biasanya ditetapkan oleh huruf x, sementara imej mereka adalah surat dan. Sebaliknya, kepada peraturan surat -menyurat yang menghubungkannya juga dipanggil dengan beberapa huruf abjad lain, seperti fungsi "f", walaupun yang lain dapat digunakan.  Dalam notasi padat ia ditulis:

f: x → y = f (x)

Rajah 1. Graf fungsi polinomial sebenar

Kepada pemboleh ubah  x ia dikenali sebagai pembolehubah bebas, Sementara dan Ia adalah pemboleh ubah bergantung. Fungsi ini boleh dinyatakan dalam beberapa cara, contohnya melalui pernyataan matematik seperti ini:

• F (x) = 2x -3
• H (x) = -3x²
• 

Satu lagi bentuk ungkapan adalah melalui graf, yang sangat berguna kerana ia membolehkan anda menghargai tingkah laku fungsi sekilas. Membina graf sangat mudah menggunakan sistem koordinat Cartesian, di mana rakan sebaya [x, f (x)] diwakili sebagai titik dalam pesawat. Kemudian mereka bergabung dengan garis lembut dan berterusan, anda dapat melihat bagaimana fungsi itu.

Contoh

Untuk membina graf yang anda boleh menggunakan jadual nilai di mana titik ke graf diletakkan. Untuk nilai x yang berubah -ubah dipilih yang tergolong dalam domain fungsi, iaitu, yang apabila digantikan dalam formula, seterusnya menunjukkan nombor sebenar.

Setelah nilai x telah dipilih, imejnya y = f (x) ditentukan, dan dengan cara ini pasangan mata [x, f (x)] diperolehi yang akan menjadi grafik.

Boleh melayani anda: Fungsi homografi: Cara graf, latihan yang diselesaikan

Terdapat beberapa perkara yang penting dan harus dimasukkan ke dalam jadual: yang grafik memotong ke paksi koordinat, jika mereka wujud, kerana tidak semua fungsi bersilang mereka.

Untuk mengira mereka, teruskan seperti berikut:

-Persimpangan dengan paksi dan: x = 0 dibuat dalam formula fungsi dan nilai yang sepadan dikira.

-Persimpangan dengan paksi x: Y = 0 dilakukan dan persamaan f (x) = 0 diselesaikan.

Seterusnya, sistem koordinat Cartesian ditarik dan setiap titik diplotkan, yang kemudiannya bergabung dengan garis lembut dan berterusan jika boleh.

Contoh 1

Bina jadual nilai dan graf fungsi berikut:

f (x) = x² -4

Sebelum memulakan, anda perlu mencari domain fungsi, yang merupakan set nilai sebenar yang mana fungsi itu wujud. Memandangkan ia adalah fungsi kuadratik, sebarang nilai x yang dimiliki oleh nombor sebenar mempunyai imej sebenar, menurut f (x).

Kemudian, jadual boleh dibina dengan memilih sebarang nilai x, dan perkara yang paling mudah adalah bermula dengan persimpangan graf dengan paksi, jika ada. Setelah mencari mereka, maka mata -mata lain dicari untuk melengkapkan jadual.

Untuk x = 0

f (0) = -4

Oleh itu, titik pertama dalam jadual adalah (0, -4). Ini adalah persimpangan graf dengan paksi dan.

Untuk y = 0

Maka y = 0 dilakukan dan persamaan yang hasilnya diselesaikan:

x² -4 = 0

x² = 4

Penyelesaian persamaan ini adalah: x₁= 2 dan x₂= -2. Oleh itu terdapat dua persimpangan dengan paksi x, yang merupakan titik: (-2.0) dan (2.0).

Boleh melayani anda: nombor sempurna: bagaimana mengenal pasti dan contohnya

Sekarang anda boleh mencari lebih banyak mata untuk ditambah ke jadual nilai:

Untuk x = 1

F (1) = (1)² - 4 = -3

Untuk x = - 1

F (-1) = (-1)² - 4 = -3

Untuk x =  3

F (3) = (3)² - 4 = 5

Untuk x =  -3

F (-3) = (-3)² - 4 = 5

Jadual Nilai

Jadual berikut menunjukkan mata yang diperoleh, yang akan berfungsi untuk membina graf f (x):

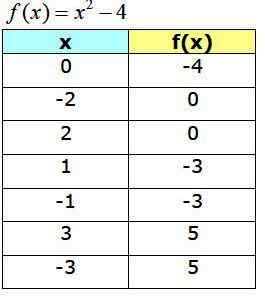Fungsi graf f (x) = x² -4

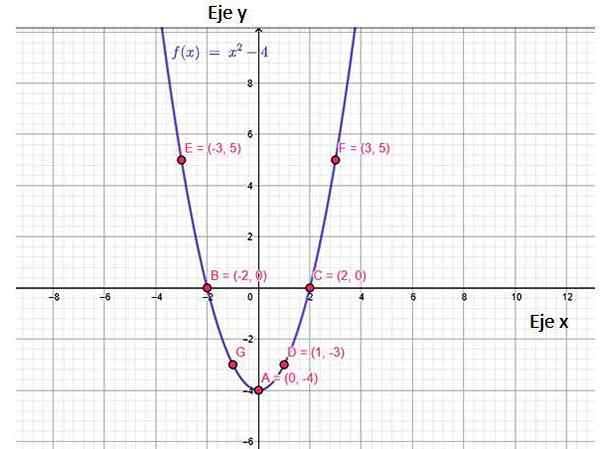Rajah 2. Fungsi f (x) graf fungsi, menunjukkan beberapa perkara yang dimiliki olehnya, termasuk persimpangan dengan paksi. Sumber: f. Zapata, melalui Geogebra.

Grafik fungsi ini adalah perumpamaan, yang dibuka dan mempunyai titik minimum, yang dipanggil puncak, koordinat (0, -4). Sangat menarik untuk diperhatikan bahawa nilai f (x) bermula pada y = -4 hingga ∞. Ini adalah julat fungsi.

Grafik dapat disimpulkan bahawa fungsi itu berterusan, berkurangan dalam selang (-∞, 0) dan meningkat dari sana.

Contoh 2

Memiliki carta fungsi adalah mungkin untuk mengetahui domainnya, julatnya, persimpangan yang ada dengan paksi dan menggambarkan tingkah laku umum (pertumbuhan dan penurunan).

Berikut adalah graf fungsi polinomial:

f (x) = - x⁴+4x²+1

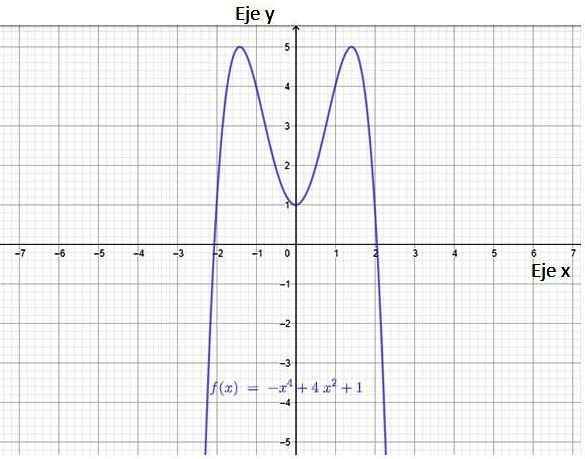Rajah 3. Graf fungsi polinomial. Sumber: f. Zapata melalui geogebra.

Dari imej ia mengikuti bahawa fungsi mempunyai dua persimpangan dengan paksi x, mata (-2.0) dan (2.0). Ia juga mempunyai persimpangan dengan paksi y, titik (0.1).

Domain fungsi polinomial adalah set lengkap nombor sebenar, ia juga memberi amaran bahawa fungsi itu berterusan dan mempunyai simetri di sekitar paksi menegak. Sesungguhnya, dapat disahkan bahawa fungsi ini Simetri untuk. Fungsi adalah walaupun ia memenuhi:

Boleh melayani anda: teorem hijau, demonstrasi, aplikasi dan latihan

f (x) = f (-x)

Pembaca dapat mengesahkan bahawa dengan mengganti -x dalam fungsi, ia tidak diubah.

Terdapat dua titik menarik, yang berada pada ketinggian y = 5, adalah nilai maksimum fungsi. Julat fungsi ini, ia.

Untuk mengetahui nilai x yang imejnya adalah y = 5, nilai ini digantikan dalam fungsi:

5 = - x⁴+4x²+1

Dan persamaan ini diperoleh:

- x⁴ + 4x² - 4 = 0

Penyelesaiannya adalah -√2 dan + √2. Nah, fungsinya adalah:

-Tumbuh Dari x -∞ hingga x = -√2

-Berkurangan Dari x = -√2 hingga x = 0

-Tumbuh Dari x = 0 hingga x = + √2

-Berkurangan Dari x = + √2 dan seterusnya.

Latihan diselesaikan

Bina graf fungsi berikut:

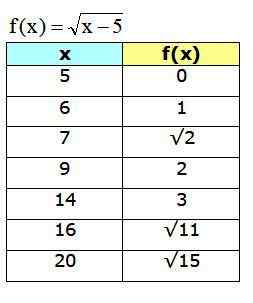
f (x) = √ (x-5)

Penyelesaian

Pertama anda perlu menentukan domain fungsi, untuk mengetahui nilai -nilai x yang boleh dipilih untuk membina jadual. Dalam kes fungsi yang dicadangkan, jumlah dalam akar mestilah positif atau sama dengan 0, oleh itu:

x - 5 ≥ 0

x ≥ 5

Oleh itu, hanya nilai yang lebih besar daripada atau sama dengan 5 boleh dipilih untuk jadual. Bagi persimpangan dengan paksi koordinat, satu -satunya kemungkinan adalah melakukan y = 0, dan kemudian x = 5.

Tidak berguna untuk melakukan x = 0 untuk fungsi ini, kerana nilai ini bukan milik domain.

Grafik yang diperoleh adalah:

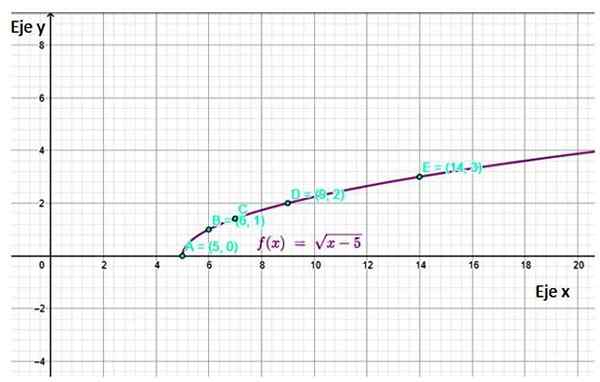Rajah 4. Fungsi graf f (x) menunjukkan beberapa mata yang dikira dalam jadual. Sumber: f. Zapata melalui geogebra.

Rujukan

1. Zon e-math. Jenis fungsi. Pulih dari: emathzone.com.
2. Hoffman, J.G. Pemilihan masalah matematik. Ed. Spphinx.
3. Matematik menyeronokkan. Rujukan fungsi Commons. Pulih dari: Mathisfun.com.
4. Requena, b. Formula Universe. Jenis fungsi. Pulih dari: universoformulas.com.
5. Stewart, J. 2006. Preccculment: Matematik untuk Pengiraan. 5th. Edisi. Pembelajaran Cengage.