Jenis fungsi transenden, definisi, sifat, contoh

The fungsi transenden Elemen adalah fungsi eksponen, logaritma, trigonometrik, songsang, hiperbolik dan hyperbolic songsang. Iaitu, mereka adalah yang tidak dapat dinyatakan oleh nisbah polinomial, polinomial atau polinomial. 

Fungsi transenden yang tidak berkepentingan juga dikenali sebagai fungsi khas dan di antara mereka fungsi ralat boleh dinamakan. The Fungsi algebra (Polinomial, Polynomial Quotients dan Polynomial Roots) di sebelah fungsi transenden unsur -unsur membentuk apa yang dalam matematik dikenali sebagai fungsi asas.

Ia juga dianggap fungsi transenden yang dihasilkan dari operasi antara fungsi transenden atau antara fungsi transenden dan algebra. Operasi ini adalah: jumlah dan perbezaan fungsi, produk dan nisbah fungsi, serta komposisi dua atau lebih fungsi.

[TOC]

Definisi dan sifat

Fungsi eksponen

Ia adalah fungsi sebenar pemboleh ubah bebas sebenar bentuk:

f (x) = a^x = a^x

di mana ke Ia adalah nombor sebenar yang positif (A> 0) tetap dipanggil pangkalan. Circumflejo atau pengawasan digunakan untuk menunjukkan operasi potentiasi.

Mari kita masukkan A = 2 Maka fungsinya seperti ini:

f (x) = 2^x = 2^x

Yang akan dinilai untuk beberapa nilai pembolehubah bebas x:

Berikut adalah grafik di mana fungsi eksponen untuk beberapa nilai asas diwakili, termasuk asas dan (Nombor NEPER dan ≃ 2.72). Asas dan Sangat penting, secara umum, ketika bercakap mengenai fungsi eksponen, anda memikirkan E^x, yang juga dilambangkan exp (x).

Rajah 1. Fungsi eksponen a^x, untuk beberapa nilai asas a. (Huraian sendiri)

Sifat fungsi eksponen

Dari Rajah 1 dapat dilihat bahawa domain fungsi eksponen adalah nombor nyata (dom f = R) dan julat atau laluan adalah yang sebenar yang positif (berlari f = R⁺). 

Boleh melayani anda: simetri

Sebaliknya, tanpa mengira nilai asas A, semua fungsi eksponen melalui titik (0, 1) dan oleh titik (1, a). 

Apabila asas A> 1, Maka fungsi semakin meningkat dan ketika 0 < a < 1 Fungsi ini berkurangan. 

Lengkung y = a^x dan dari y = (1/a)^x  Mereka simetri berkenaan dengan paksi Dan. 

Dengan pengecualian kes itu A = 1, Fungsi eksponen adalah injak, iaitu, untuk setiap nilai imej, satu sepadan dan hanya nilai permulaan.

Fungsi logaritma

Ini adalah fungsi sebenar yang sebenar bagi pemboleh ubah bebas sebenar berdasarkan definisi logaritma nombor. Berasaskan logaritma ke nombor x, Itu nombornya dan yang mana asas mesti dinaikkan untuk mendapatkan hujah x:

log_ke(x) = y ⇔ a^y = x

Iaitu, fungsi logaritma di pangkalan ke Ia adalah fungsi songsang kepada fungsi eksponen berdasarkan ke.

Sebagai contoh:

log₂1 = 0, kerana 2^0 = 1

Kes lain, log₂4 = 2, kerana 2^2 = 4

Logaritma akar 2 adalah log₂√2 = ½, kerana 2^½ = √2

log₂ ¼ = -2, memandangkan bahawa 2^(-2) = ¼ 

Berikut adalah graf fungsi logaritma di pelbagai pangkalan.

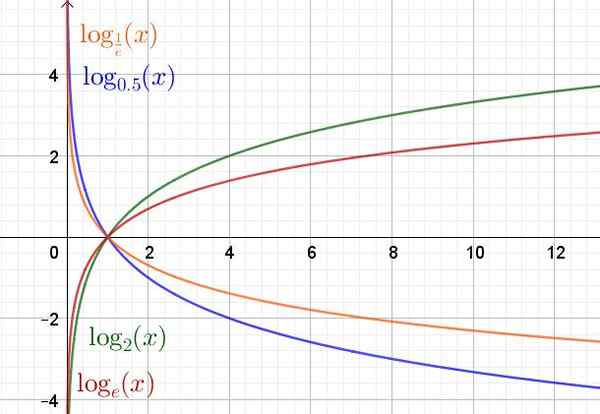Rajah 2. Fungsi eksponen untuk nilai asas yang berbeza. (Huraian sendiri)

Ciri -ciri fungsi logaritmo

Domain fungsi logaritma dan (x) = logke(x)  Mereka adalah nombor sebenar positif R+. Julat atau laluan adalah nombor sebenar R.

Tidak kira asasnya, fungsi logaritma selalu melalui titik (1.0) dan titik (a, 1) tergolong dalam graf fungsi tersebut.

Ia dapat melayani anda: Teori giliran: sejarah, model, apa itu dan contoh untuk

Sekiranya asas A lebih besar daripada unit (a> 1) fungsi logaritma semakin meningkat. Tetapi ya (0 < a < 1) entonces es una función decreciente.

Seno, Coseno dan Fungsi Tangen

Fungsi sinus memberikan nombor sebenar dan setiap nilai x, di mana x mewakili ukuran sudut dalam radianes. Untuk mendapatkan nilai sen (x) dari sudut, sudut diwakili dalam lingkaran unit dan unjuran sudut tersebut pada paksi menegak adalah payudara yang sepadan dengan sudut itu.

Di bawah adalah (dalam Rajah 3) bulatan trigonometri dan payudara untuk beberapa nilai sudut x1, x2, x3 dan x4.

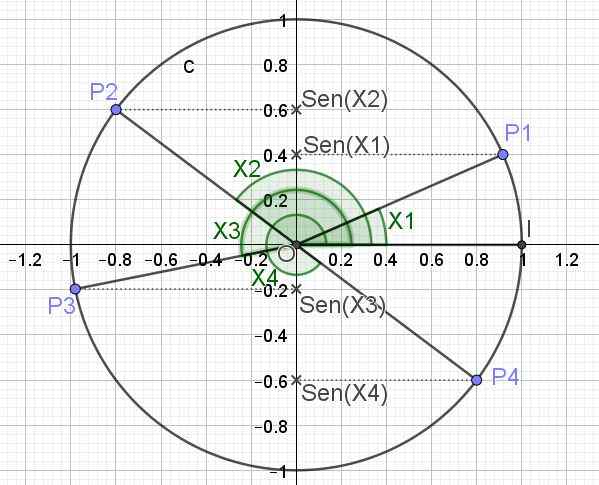Rajah 3. Bulatan trigonometri dan pangkuan beberapa sudut. (Huraian sendiri)

Ditakrifkan dengan cara ini nilai maksimum yang boleh dimiliki oleh fungsi sen (x) ialah 1, yang berlaku apabila x = π/2 + 2π n, iaitu n integer (0, ± 1, ± 2,). Nilai minimum yang dapat dilakukan oleh fungsi sen (x) apabila x = 3π/2 + 2π n. 

Fungsi coseno y = cos (x) ditakrifkan dengan cara yang sama, tetapi unjuran kedudukan sudut P1, P2, dan lain -lain dilakukan pada paksi mendatar bulatan trigonometri.

Sebaliknya, fungsi y = tan (x) adalah nisbah antara fungsi sinus dan fungsi kosinus.

Kemudian graf fungsi transenden sen (x), cos (x) dan tan (x) ditunjukkan

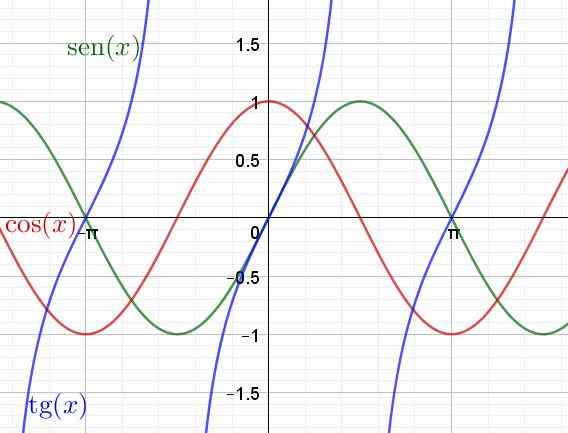Rajah 4. Graf fungsi transenden, payudara, kosinus dan tangen. (Huraian sendiri)

Diperoleh dan integral

Berasal dari fungsi eksponen

Derivatif dan ' fungsi eksponen y = a^x Ia adalah fungsi a^x didarabkan olehnya Logaritma Neperian asas a:

Boleh melayani anda: Tetapkan Teori: Ciri, Elemen, Contoh, Latihan

dan '= (a^x)' = a^x ln a

Dalam kes tertentu asas dan, Derivatif fungsi eksponen adalah fungsi eksponen itu sendiri.

Integral fungsi eksponen

Integral tak terbatas dari a^x Ia adalah fungsi yang dibahagikan antara logaritma neperian asas. 

Dalam kes asas E, integral fungsi eksponen adalah fungsi eksponen itu sendiri.

Jadual derivatif dan integral fungsi transenden

Berikut adalah jadual ringkasan fungsi transenden utama, derivatif dan tidak terbatas (antiderivatif):

Jadual derivatif dan integral yang tidak terbatas untuk beberapa fungsi transenden. (Huraian sendiri)

Contoh

Contoh 1

Cari fungsi yang dihasilkan komposisi fungsi f (x) = x^3 dengan fungsi g (x) = cos (x):

(f atau g) (x) = f (g (x)) = cos³(x)

Derivatif dan integralnya tidak terbatas adalah:

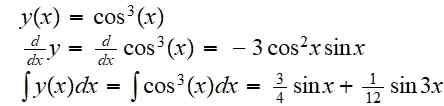
Contoh 2

Cari komposisi fungsi g dengan fungsi f, iaitu G dan F fungsi yang ditakrifkan dalam contoh sebelumnya:

(g atau f) (x) = g (f (x)) = cos (x³)

Harus diperhatikan bahawa komposisi fungsi bukan operasi komutatif.

Derivatif dan integral yang tidak terbatas untuk fungsi ini masing -masing:

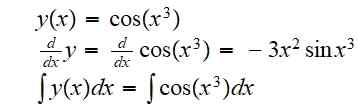
Integral dibiarkan ditunjukkan kerana tidak mungkin untuk menulis hasilnya sebagai gabungan fungsi asas dengan cara yang tepat.

Rujukan

1. Kalkulus pemboleh ubah tunggal. Ron Larson, Bruce H. Edwards. Pembelajaran Cengage, 10 November. 2008
2. Teorem Fungsi Terbitan: Sejarah, Teori, dan Aplikasi. Steven G. Krantz, Harold R. Taman. Springer Science & Business Media, 9 Nov. 2012
3. Analisis multivariable. Sable Shirali, Hararkrishan Lal Vasudeva. Springer Science & Business Media, 13 Disember. 2010
4. Dinamik Sistem: Pemodelan, Simulasi, dan Kawalan Sistem Mekatronik. Dekan c. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7 mar. 2012
5. Kalkulus: Matematik dan pemodelan. William Bauldry, Joseph R. Fiedler, Frank R.Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1 Januari. 1999
6. Wikipedia. Fungsi transenden. Pulih dari: Adakah.Wikipedia.com