Matematik

Geometri Euclidian

Geometri Euclidian

Kami menerangkan apa geometri Euclidian, sejarah, elemen dan kami memberikan beberapa contoh adalah

Euclid of Alexandria dan unsur -unsurnya, oleh Jusepe de Ribera, di sebelah, dua garis bukan selaras dan garis yang memotongnya, menggambarkan postulat kelima. Sumber: Wikimedia Commons.

Apakah geometri Euclidian?

The Geometri Euclidian Ia adalah yang ditadbir oleh mereka yang berpose oleh Euclid de Alejandría, geometer Yunani yang hidup ke arah 300 hingga.C, yang menghormati disiplin ini dinamakan, kerana ia adalah yang pertama untuk sistematinya.

Cabang matematik ini mengkaji sifat -sifat garis, pesawat, sudut dan angka geometri seperti poligon, lilitan dan conics lain. Oleh itu, kepentingannya dalam sains dan kejuruteraan, yang perkembangannya mendorong dengan ketara.

Sebaliknya, geometri Euclidean adalah sains yang tepat, kerana dengan itu jalan sistematisasi sains bermula, serta penggunaan logik untuk menunjukkan, dari beberapa aksioma, banyak proposisi yang disebut teorem, untuk menggambarkan sifat -sifatnya objek geometri.

Sejarah

Geometri mempunyai sejarah yang panjang, kerana kepentingan kemanusiaan di dalamnya sangat tua dan paksi pusat geometri Euclidean adalah kerja Item, dari Euclid Alexandria yang bijak, sebuah bandar yang terletak di Mesir, dan yang tinggal di abad keempat hingga.C.

Pada masa itu sifat -sifat yang paling penting dari banyak angka dan badan geometri diketahui. Terdapat pengetahuan yang luas tentang geometri, tetapi semuanya adalah empirikal dan kekurangan sistematisasi.

Kemudian, raja Mesir Ptolemy dan mempercayakan guru Euclid yang sudah terkenal, yang sekolahnya berada di Alexandria, untuk menganjurkan semua pengetahuan matematik dan geometri yang ada setakat ini, termasuk teorem dan sifat.

Euclides terpaksa bekerja dan bersebelahan dengan murid -murid -Nya, menulis unsur -unsur kerjanya, yang dibahagikan kepada tiga belas buku, sebagai bab. Kerja ini akan menjadi rujukan untuk geometri untuk generasi akan datang.

Boleh melayani anda: derivatif berturut -turut

Unsur -unsur Euclid

Kandungan unsur -unsur dianjurkan seperti berikut:

  • Dalam Buku I hingga IV Geometri rata berkembang.
  • Dalam Buku V dan saya melihat teori perkadaran.
  • Buku IX didedikasikan untuk aritmetik.
  • Tidak dapat dinafikan muncul dalam Buku x,
  • Geometri ruang dalam buku xi hingga xiii.

Geometri Euclidean adalah asas bagi banyak perkembangan geometri posterior dan kini diajar di semua sekolah di dunia.

Ia juga mempunyai kebaikan menjadi kerja pertama untuk memasukkan demonstrasi yang teliti berdasarkan penalaran logik, dan juga dalam memberikan koheren kepada badan pengetahuan geometri dan matematik pada masa itu.

Unsur Asas Geometri Euclidean

Geometri Euclidean dibina sekitar empat elemen asas, yang diterangkan dalam Buku I unsur -unsur:

  1. Tempat
  2. Lurus
  3. Rata
  4. Ruang

1. Tempat

A tempat Ia tidak mempunyai dimensi atau bahagian dan dibezakan dari titik lain hanya di lokasinya. Jika dua mata A dan B berbeza, ia adalah kerana mereka mempunyai kedudukan yang berbeza, yang ditunjukkan melalui koordinat Cartesian yang terkenal (x, y) jika titik itu berada dalam satah, atau koordinat (x, y, z) Sekiranya berada di ruang angkasa.

Perlu diperhatikan bahawa sistem Cartesian bukan sebahagian daripada Item dari Euclid, tetapi muncul kemudian dalam 1600 tahun dan disebabkan oleh René Descartes.

2. Lurus

The lurus Ia adalah koleksi mata yang tidak terhingga, dan hanya mempunyai panjang, bukan lebar. Sebahagian daripadanya biasanya ditarik, dengan anak panah dalam kedua -dua menunjukkan bahawa garis itu berterusan selama -lamanya.

3. Rata

A rata Ia adalah permukaan yang tidak terhad, jadi ia mempunyai dua dimensi dan yang mana sebahagiannya diwakili, dengan cara persegi atau segi empat tepat.

Di sana, dalam satah, terdapat banyak angka geometri, seperti garis, lengkung terbuka dan tertutup dan poligon, antara lain.

Boleh melayani anda: persamaan umum garis yang cerunnya sama dengan 2/3

4. Ruang

Akhirnya, ada ruang Dengan tiga dimensi, mampu menempatkan semua mata. Ia mengandungi pesawat dan badan geometri yang dicirikan oleh jumlahnya, seperti polyhedra, sfera dan banyak lagi.

Ini boleh dianggap sebagai definisi asas geometri Euclidean, tetapi sebagai tambahan kepada ini, Euclides menawarkan kira -kira 150 definisi yang bervariasi dalam kerja mereka.

Tanggapan umum

Mereka terdiri daripada fakta yang jelas dan intuitif, yang tidak sesuai dengan skop geometri dan digunakan sebagai konsep berkembang. Mereka merujuk kepada "perkara" dalam konteks yang sangat luas:

  1. Perkara yang sama dengan yang lain, mereka sama antara satu sama lain.
  2. Sekiranya perkara ditambah kepada satu lagi perkara, dan semuanya adalah sama, hasilnya juga sama.
  3. Sekiranya perkara yang sama dicuri, selebihnya juga sama.
  4. Apabila keadaan bertepatan antara satu sama lain, itu kerana mereka sama.
  5. Seluruhnya selalu lebih besar daripada pihak -pihak, diambil secara berasingan.

Postulates geometri Euclidean

Postulat atau aksioma adalah pernyataan mudah yang dianggap benar dan jelas, jadi mereka tidak memerlukan demonstrasi.

Mereka menjadi asas geometri Euclidian dan Euclid menetapkan lima dalam buku mereka I:

  1. Jadilah dua mata yang berbeza ke dan B, hanya ada satu baris yang melewati mereka, iaitu, dua mata menentukan garis.
  2. Sebarang segmen rectilinear dapat dilanjutkan selama -lamanya untuk membentuk garis, oleh itu, setiap segmen milik garis.
  3. Sekiranya anda mempunyai dua mata yang berbeza atau A, anda sentiasa boleh melukis bulatan dengan pusat di O dan radius sama dengan segmen OA.
  4. Semua sudut lurus bersesuaian antara satu sama lain.
  5. Diberi garis dan titik p yang bukan miliknya, selalu mungkin.

Postulat terakhir, terutamanya dalam versi asalnya, tidak kelihatan semudah yang lain. Ia menyatakan bahawa:

Boleh melayani anda: heptagon

"Sekiranya garis lurus yang jatuh pada dua baris lain, menjadikan kedua -dua sudut pedalaman di sisi yang sama kurang dari dua sudut lurus, kata garis lurus, meluas selama -lamanya, mereka (bersilang) di sisi di mana sudut kecil adalah bahawa dua sudut lurus ".

Iaitu, pada mulanya postulate 5 menetapkan keadaan supaya dua baris tidak selari. Tetapi lebih jelas apabila ditulis sedemikian rupa sehingga ia menggambarkan sebaliknya, iaitu, paralelisme garis.

Contoh geometri Euclidean

Contoh 1

Terdapat tiga perkara yang berbeza, dilabelkan dengan huruf A, B dan C.

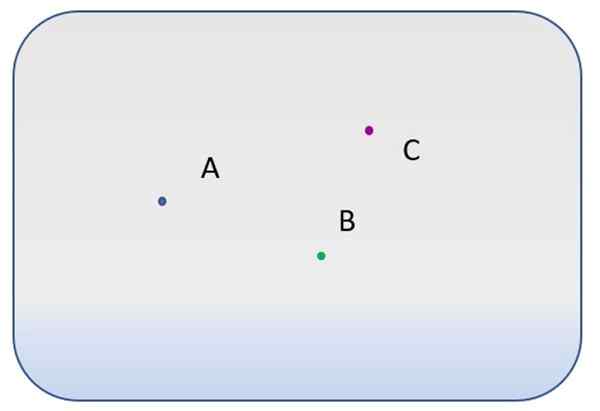
  1. Berapa banyak baris yang berlainan melalui titik a?
  2. Dan berapa banyak yang boleh ditarik antara mata a dan b? Dan antara a dan c?
  3. Adakah mungkin untuk melukis garis ke mana titik A, B dan C?

Jawapan kepada

Menurut Postulate I, garis lurus tak terhingga dapat ditarik melalui A, kerana dua titik diperlukan untuk menentukan garis.

Jawab b

Entre A dan B hanya boleh ditarik garis. Dan antara A dan C juga.

Jawab c

Tidak mungkin untuk garis mengandungi A, B dan C pada masa yang sama.

Contoh 2

Diminta untuk membina langkah demi langkah segitiga sama rata (semua sisinya sama), mengetahui salah satu sisinya, iaitu segmen ab dan menunjukkan dalam setiap langkah postulat atau tanggapan umum yang digunakan dalam pembinaan di.

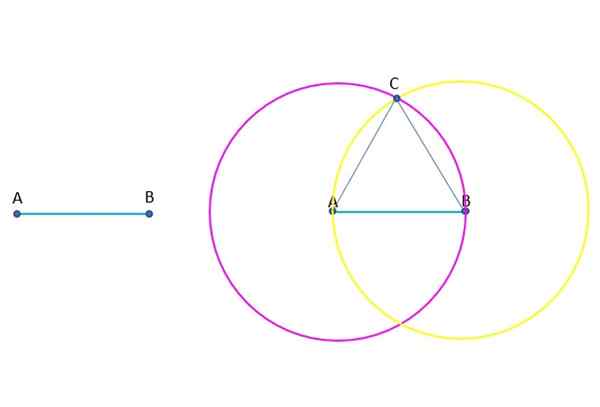Pembinaan Segitiga Segitiga ABC. Sumber: f. Zapata.

Jawapan

Langkah 1

Bulatan dengan pusat di a dan radio ab ditarik. Ini selalu mungkin, menurut Postulate III.

Langkah 2

Satu lagi lilitan dengan pusat di B dan Radio AB ditarik, dan Postulate III digunakan lagi.

Langkah 3

Kedua -dua lingkaran, yang mempunyai jejari yang sama, dipotong pada titik c. Sekarang anda boleh melukis segmen yang bersatu c dengan a dan b masing -masing, mengikut postulat i.

Segmen -segmen ini adalah radio lilitan dan oleh itu ukuran AC dan BC adalah sama dengan AB, menurut tanggapan umum 1. Maka segitiga ABC adalah sama rata.