Ijazah polinomial bagaimana ia ditentukan, contoh dan latihan

Dia tahap polinomial dalam a Pembolehubah diberikan oleh istilah yang ada di Eksponen Utama, dan jika polinomial mempunyai dua atau lebih pembolehubah, Maka ijazah ditentukan oleh jumlah eksponen setiap istilah, jumlah utama polinomial.

Mari lihat bagaimana menentukan tahap polinomial dengan cara yang praktikal.

Rajah 1. Persamaan Einstein yang terkenal untuk Tenaga E adalah gred 1 mutlak untuk pemboleh ubah massa, dilambangkan oleh m, kerana kelajuan cahaya c dianggap tetap. Sumber: PIQSELS.

Katakan polinomial p (x) = -5x + 8x³ + 7 - 4x². Polinomial ini adalah pemboleh ubah, dalam hal ini ia adalah pemboleh ubah x. Polinomial ini terdiri daripada beberapa istilah, yang berikut:

-5x; 8x³; 7; - 4x²

 Mari kita pilih dari empat istilah yang eksponennya lebih besar, istilah ini adalah:

8x³

Dan sekarang apakah eksponennya? Jawapannya ialah 3. Oleh itu p (x) adalah polinomial gred 3.

Sekiranya polinomial yang dipersoalkan mempunyai lebih daripada satu pemboleh ubah, maka ijazahnya boleh:

-Mutlak

-Berhubung dengan pemboleh ubah

Ijazah mutlak dijelaskan pada mulanya: menambah eksponen setiap istilah dan memilih yang terbesar.

Sebaliknya, tahap polinomial berkenaan dengan salah satu pembolehubah atau huruf, adalah nilai terbesar eksponen yang telah mengatakan surat. Titik akan lebih jelas dengan contoh dan latihan yang diselesaikan dari bahagian berikut.

[TOC]

Contoh gred polinomial

Polinomial boleh diklasifikasikan dengan ijazah, dapat menjadi ijazah pertama, gred kedua, gred ketiga dan sebagainya. Untuk contoh Rajah 1, tenaga adalah monomial yang pertama untuk jisim.

Boleh melayani anda: Congruence: angka kongruen, kriteria, contoh, latihan

Ia juga penting untuk melihat bahawa bilangan istilah yang mempunyai polinomial sama dengan ijazah ditambah 1. Jadi:

-Polinomial darjah pertama mempunyai 2 istilah: a₁x + a_{Sama ada}

-Polinomial kedua -dua mempunyai 3 istilah: a₂x² + ke₁x + a_{Sama ada}

-Polinomial darjah ketiga mempunyai 4 istilah: a₃x³ + ke₂x² + ke₁x + a_{Sama ada}

Dan sebagainya. Pembaca yang penuh perhatian akan mendapati bahawa polinomial contoh -contoh sebelumnya ditulis dengan cara yang menurun, iaitu, pertama kali meletakkan istilah dengan ijazah utama.

Pelbagai polinomial muncul dalam jadual berikut, baik dari satu dan beberapa pembolehubah dan darjah mutlak masing -masing:

Jadual 1. Contoh polinomial dan darjah mereka

Polinomial	Ijazah
3x4+5x3-2x+3	4
7x3-2x2+3x-6	3
6	0
X-1	1
x5-Bx4+Abx3+Ab3x2	6
3x3dan5 + 5x2dan4 - 7xy2 + 6	8

Dua polinomial terakhir mempunyai lebih daripada satu pemboleh ubah. Istilah yang mempunyai ijazah mutlak terbesar telah menonjol dengan berani, sehingga pembaca dengan cepat memeriksa ijazah. Penting untuk diingat bahawa apabila pemboleh ubah tidak mempunyai eksponen bertulis, difahami bahawa eksponen tersebut sama dengan 1.

Contohnya dalam istilah yang menonjol Ab³x² Terdapat tiga pembolehubah, iaitu: ke, b dan x. Dalam istilah itu, ke Ia dinaikkan kepada 1, iaitu:

a = a¹

Oleh itu Ab³x² = a¹b³x²

Oleh kerana eksponen B adalah 3 dan X adalah 2, ia segera diikuti bahawa tahap istilah ini adalah:

1+3+2 = 6

Dan ia adalah tahap polinomial mutlak, kerana tiada istilah lain mempunyai tahap yang lebih tinggi.

Prosedur untuk bekerja dengan polinomial

Apabila bekerja dengan polinomial, penting untuk memberi perhatian kepada tahap yang sama, kerana di tempat pertama dan sebelum melakukan sebarang operasi, mudah untuk mengikuti langkah -langkah ini, yang mana ijazah memberikan maklumat yang sangat penting:

-Memerintahkan polinomial keutamaan dalam pengertian yang semakin berkurangan. Dengan cara ini, istilah dengan gred tertinggi adalah di sebelah kiri dan yang paling rendah ke kanan.

Boleh melayani anda: endecagon

-Kurangkan istilah yang sama, prosedur yang terdiri daripada menambahkan semua syarat pemboleh ubah dan ijazah yang sama yang berada dalam ungkapan secara algebra.

-Sekiranya perlu, polinomial selesai, istilah interspersing yang pekali adalah 0, sekiranya terma dengan beberapa eksponen.

Memerintahkan, mengurangkan dan melengkapkan polinomial

Memandangkan polinomial p (x) = 6x² - 5x⁴- 2x+3x+7+2x⁵  - 3x³ + x⁷ -12 diminta untuk memerintahkannya dengan menurun, mengurangkan istilah yang sama jika ada dan menyelesaikan terma yang hilang dari tepat.

Perkara pertama yang perlu dicari adalah istilah dengan eksponen utama, yang merupakan tahap polinomial, yang ternyata:

x⁷

Oleh itu p (x) adalah gred 7. Kemudian polinomial diperintahkan, bermula dengan istilah ini ke kiri:

P (x) = x⁷ + 2x⁵ - 5x⁴ - 3x³ + 6x² - 2x+3x+7 -12

Istilah yang serupa kini dikurangkan, yang berikut: - 2x dan 3x di satu pihak. Dan 7 dan -12 di sisi lain. Untuk mengurangkannya, koefisien ditambah secara algebra dan pemboleh ubah tidak berubah (jika pembolehubah tidak muncul di sebelah pekali, harus diingat bahawa x⁰ = 1):

-2x+3x = x

7 -12 = -5

Keputusan ini digantikan dalam p (x):

P (x) = x⁷ +2x⁵ - 5x⁴ - 3x³ + 6x² + x -5

Dan akhirnya polinomial diperiksa untuk melihat sama ada eksponen hilang dan berkuatkuasa, istilah yang eksponennya 6 hilang, oleh itu ia selesai dengan sifar seperti ini:

P (x) = x⁷ + 0x⁶ +2x⁵ - 5x⁴ - 3x³ + 6x² + X - 5

Sekarang diperhatikan bahawa polinomial ditinggalkan dengan 8 istilah, kerana seperti yang dikatakan sebelumnya, bilangan istilah adalah sama dengan ijazah + 1.

Kepentingan tahap polinomial dalam jumlah dan penolakan

Dengan polinomial, operasi jumlah dan penolakan boleh dilakukan, di mana hanya istilah yang serupa ditambah atau dikurangkan, yang merupakan pemboleh ubah yang sama dan tahap yang sama. Sekiranya tidak ada istilah yang serupa, jumlah atau penolakan dibiarkan hanya ditunjukkan.

Boleh melayani anda: harta pengedaran

Sebaik sahaja jumlah atau penolakan telah dilakukan, yang terakhir adalah jumlah yang bertentangan, tahap polinomial yang dihasilkan selalu sama dengan atau kurang daripada tahap penambahan polinomial yang lebih tinggi.

Latihan yang diselesaikan

- Latihan diselesaikan 1

Cari jumlah berikut dan tentukan tahap mutlaknya:

ke³- 8ax²  + x³ + 5th²X - 6ax² - x³ + Ke -3³ - 5th²x - x³ + ke³+ 14ax² - x³

Penyelesaian

Ia adalah polinomial dua pembolehubah, jadi mudah untuk mengurangkan istilah yang sama:

ke³- 8ax²  + x³ + 5th²X - 6ax² - x³ + Ke -3³ - 5th²x - x³ + ke³+ 14ax² - x³ =

= a³ + Ke -3³ + ke³ - 8ax² - 6ax²+ 14ax² +5th²X - 5a²x+ x³- x³- x³- x³ =

= 5a³ - 2x³

Kedua -dua istilah adalah gred 3 dalam setiap pemboleh ubah. Oleh itu tahap polinomial mutlak adalah 3.

- Latihan diselesaikan 2

Menyatakan sebagai polinomial kawasan angka geometri rata berikut (Rajah 2 kiri). Berapakah tahap polinomial yang dihasilkan?

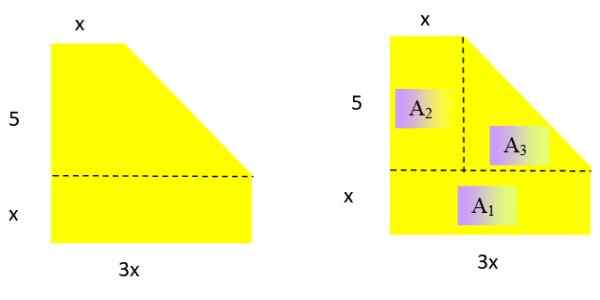Rajah 2. Di sebelah kiri, angka untuk tahun diselesaikan 2 dan ke kanan, angka yang sama diuraikan dalam tiga bidang yang ekspresinya diketahui. Sumber: f. Zapata.

Penyelesaian

Menjadi kawasan, polinomial yang dihasilkan mestilah gred 2 dalam pembolehubah x. Untuk menentukan ungkapan yang mencukupi untuk kawasan tersebut, angka itu dipecahkan ke kawasan yang diketahui:

Kawasan segi empat tepat dan segitiga masing -masing: Asas x ketinggian dan Asas x ketinggian /2

Ke₁ = x . 3x = 3x²; Ke₂ = 5 . x = 5x; Ke₃ = 5 . (2x /2) = 5x

Catatan: Pangkalan segitiga adalah 3x - x = 2x dan ketinggiannya 5.

Sekarang tiga ungkapan yang diperolehi ditambah, dengan ini anda mempunyai kawasan angka bergantung pada x:

3x² + 5x + 5x = 3x² + 10x

Rujukan

1. Baldor, a. 1974. Algebra Elementary. Kebudayaan Venezuela s.Ke.
2. Jiménez, r. 2008. Algebra. Prentice Hall.
3. Wikilibros. Polinomial. Pulih dari: Adakah. Wikibooks.org.
4. Wikipedia. Gred (polinomial). Pulih dari: Adakah.Wikipedia.org.
5. Zill, d. 1984. Algebra dan trigonometri. Mac Graw Hill.