Definisi, dimensi, koordinat hypercubo, terungkap

A Hypercubo adalah dimensi kiub n. Kes tertentu dimensi hypercubo dipanggil Testeract. Hypercubo atau N-Cubo terdiri daripada segmen lurus, semua panjang yang sama yang ortogonal di simpang mereka.

Manusia melihat ruang tiga dimensi: lebar, tinggi dan mendalam, tetapi tidak mungkin bagi kita untuk memvisualisasikan hypercubo dimensi lebih besar daripada 3. 

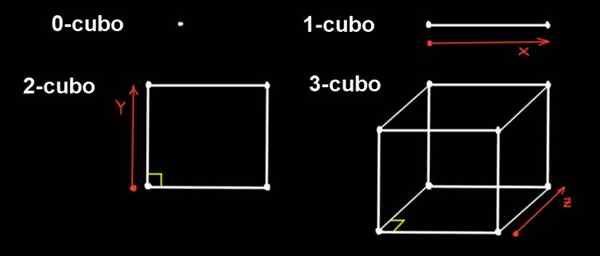
Rajah 1. 0-cubo adalah titik, jika titik itu meluas dalam satu arah jarak dengan cara 1-cubo, jika 1-cubo memanjangkan jarak ke arah ortogonal terdapat 2-cubo (dari sisi ke x a), Sekiranya 2-cubo memanjangkan jarak ke arah ortogonal terdapat 3-cubo. Sumber: f. Zapata.

Kita boleh membuat unjuran di ruang tiga dimensi untuk mewakilinya, sama seperti bagaimana kita memproyeksikan kiub di atas kapal terbang untuk mewakilinya.

Dalam dimensi 0 angka satu-satunya adalah titik, jadi 0-cubo adalah titik. 1-cubo adalah segmen lurus, yang dibentuk dengan menggerakkan titik dari jarak ke jauh.

Bagi bahagiannya 2-cubo adalah persegi. Ia dibina dengan menggantikan 1-cubo (segmen panjang a) ke arah dan, yang ortogonal ke alamat x, jarak ke.

3-cubo adalah kiub biasa. Ia dibina dari persegi yang menggantikannya dengan arah ketiga (z), yang ortogonal ke arah x dan y, jarak jauh ke.

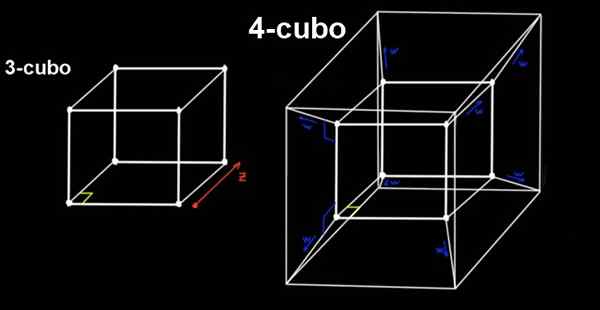Rajah 2. 4-cubo (testeract) adalah lanjutan 3-cubo dalam arah ortogonal ke tiga alamat spatial konvensional. Sumber: f. Zapata.

4-cubo adalah percubaan, yang dibina dari 3-cubo menggantikan ortogon yang sama, jarak jauh ke, ke arah dimensi keempat (atau arah keempat), yang kita tidak dapat melihat.

Pencetus mempunyai semua sudut lurus, ia mempunyai 16 simpang dan semua tepinya (18 secara keseluruhan) mempunyai panjang yang sama ke.

Jika panjang tepi n-cubo atau hypercubo dimensi n adalah 1, maka ia adalah unit hypercubo, di mana langkah-langkah pepenjuru terpanjang √n.

Boleh melayani anda: pengaturcaraan linear: Apa itu, model, sekatan, aplikasiRajah 3. N-Cubo diperolehi dari A (n-1) -cubo memanjangkannya secara ortogonal dalam dimensi seterusnya. Sumber: Wikimedia Commons.

[TOC]

Apakah dimensi?

Dimensi adalah darjah kebebasan, atau arah yang mungkin di mana objek dapat bergerak.

Dalam dimensi 0 tidak ada kemungkinan untuk bergerak dan satu -satunya objek geometri yang mungkin adalah titik.

Dimensi di ruang Euclidian diwakili oleh garis berorientasikan atau paksi yang mentakrifkan dimensi itu, yang dipanggil paksi x. Pemisahan antara dua mata a dan b ialah jarak Euclidian:

D = √ [(x_ke - x_b)²]. 

Dalam dua dimensi, ruang diwakili oleh dua garis berorientasikan ortogonal antara satu sama lain, yang dipanggil x dan paksi.

Kedudukan mana -mana titik dalam ruang dua dimensi ini diberikan oleh sepasang koordinat Cartesian (x, y) dan jarak antara dua mata a dan b ada:

D = √ [(x_ke - x_b)² + (dan_ke - dan_b)²]

Kerana ia adalah ruang di mana geometri euclid dipenuhi.

Ruang tiga dimensi

Ruang tiga dimensi adalah ruang di mana kita bergerak. Ia mempunyai tiga arah: lebar, tinggi dan mendalam.

Di dalam bilik kosong, sudut tegak lurus antara satu sama lain memberikan tiga arah dan masing -masing kita boleh mengaitkan paksi: x, y, z.

Ruang ini juga Euclidian dan jarak antara dua mata A dan B dikira seperti berikut:

D = √ [(x_ke - x_b)² + (dan_ke - dan_b)² + (z_ke - z_b)²]

Manusia tidak dapat melihat lebih daripada tiga dimensi ruang (atau euclideas).

Walau bagaimanapun, dari sudut pandangan matematik yang ketat, mungkin.

Di ruang ini satu titik mempunyai koordinat: (x1, x2, x3, ..., xn) dan jarak antara dua mata adalah: 

D = √ [(x_1st - x_{1 b})² + (x₂ - x_2b)² +... + (x_na - x_Nb)²].

Boleh melayani anda: Pengedaran Hypergeometric: Formula, Persamaan, Model

Dimensi keempat dan masa

Sesungguhnya, dalam teori masa relativiti dianggap sebagai satu lagi dimensi dan koordinat dikaitkan.

Tetapi mesti dijelaskan bahawa koordinat ini yang berkaitan dengan masa adalah nombor khayalan. Oleh itu pemisahan dua mata atau peristiwa dalam ruang masa bukan Euclidiana, tetapi mengikuti metrik Lorentz.

Hypercubo empat dimensi (pencetus) tidak hidup dalam ruang ruang, tergolong dalam ruang hiper euclideal empat dimensi. 

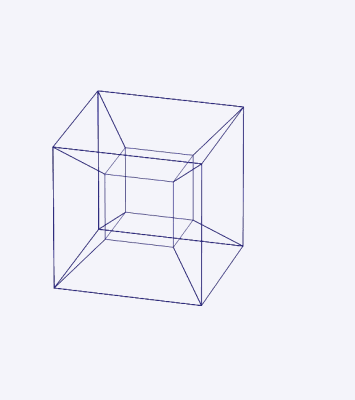
Rajah 4. Unjuran 3D Hypercubo empat dimensi dalam putaran mudah di sekitar satah yang membahagikan angka depan ke kiri, kembali ke kanan dan dari atas ke bawah. Sumber: Wikimedia Commons.

Koordinat hypercubo

Koordinat simpang N-Cubo yang berpusat pada asalnya dicapai dengan membuat semua permutasi yang mungkin dari ungkapan berikut:

(A/2) (± 1, ± 1, ± 1, .. ., ± 1)

Di mana A adalah panjang tepi.

-Dia kelantangan Dari tepi tepi adalah: (a/2)ⁿ (2ⁿ) = aⁿ.

-The pepenjuru terpanjang Ia adalah jarak antara simpang bertentangan.

-Berikut adalah simpul bertentangan di persegi: (-1, -1) dan (+1, +1).

-Dan dalam a Kiub: (-1, -1, -1) dan (+1, +1, +1). 

-The pepenjuru terpanjang langkah n-cubo: 

D = √ [1 -(-1))² +... + (1 -(-1))²] = √ [n 2²] = 2√n

Dalam kes ini, diandaikan bahawa sisi adalah A = 2. Untuk sisi N-Cubo kepada sesiapa sahaja akan kekal:

d = a√n.

-Percubaan mempunyai masing -masing 16 simpang yang disambungkan ke empat tepi. Angka berikut menunjukkan bagaimana simpang disambungkan dalam pencetus.

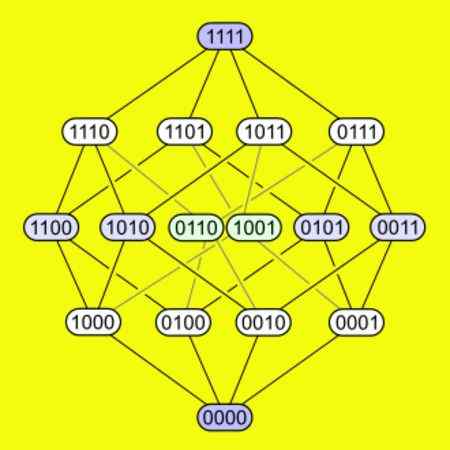Rajah 5. 16 simpang hypercubo empat dimensi ditunjukkan dan bagaimana mereka menyambung sama. Sumber: Wikimedia Commons.

Terletak di hypercubo

Angka geometri biasa, contohnya polyhedron, boleh dibentangkan dalam beberapa angka dimensi yang lebih rendah.

Dalam kes 2-cubo (satu persegi) boleh dibentangkan dalam empat segmen, iaitu empat 1-cubo.

Ia boleh melayani anda: Pengedaran Poisson: Formula, Persamaan, Model, Hartanah

Begitu juga 3-cubo boleh dibentangkan dalam enam 2-cubo.

Rajah 6. N-Cubo boleh dibentangkan di beberapa (n-1) -cubos. Sumber: Wikimedia Commons.

4-cubo (testeract) boleh dibentangkan dalam lapan 3-cubo.

Animasi berikut menunjukkan pembukaan.

Rajah 7. Hypercubo 4 -dimensi boleh dibentangkan dalam lapan kiub tiga dimensi. Sumber: Wikimedia Commons. Rajah 8. Unjuran tiga dimensi dari hypercubo empat dimensi membuat putaran berganda di sekitar dua pesawat ortogonal. Sumber: Wikimedia Commons.

Rujukan

1. Budaya saintifik. Hypercubo, menggambarkan dimensi keempat. Diperolehi dari: Culturacientifica.com
2. Epsilones. Hypercubo tetradimensional atau tesseract. Pulih dari: epsilones.com
3. Perez R, Aguilera A. Kaedah untuk mendapatkan percubaan dari pembangunan hypercubo (4d). Pulih dari: Penyelidikan.jaring
4. Wikilibros. Matematik, Polyhedra, Hypercubes. Pulih dari: Adakah.Wikibooks.org
5. Wikipedia.  Hypercube. Diperoleh dari: dalam.Wikipedia.com
6. Wikipedia. Tesseract. Diperoleh dari: dalam.Wikipedia.com