Matematik

Hyperbola

2514
614
Ismael Turner

Apa itu hiperbola?

Hyperbola adalah set titik satah sehingga nilai mutlak perbezaan antara jarak ke dua titik tetap, yang disebut lampu sorot, tetap tetap. Set titik ini membentuk lengkung dengan dua cawangan yang diperhatikan dalam Rajah 1.

Terdapat titik p (x, y), foci f₁ dan f₂ dipisahkan jarak yang sama dengan 2c. Cara matematik untuk menyatakan hubungan ini adalah melalui:

$\left |d__P_1-d__P_2 \right |=constante$

Rajah 1. Hyperbola dengan paksi fokus mendatar. Sumber: f. Zapata.

Semua titik hiperbola memenuhi syarat ini, yang membawa kepada persamaan hyperbola, seperti yang akan dilihat kemudian. Titik tengah antara lampu sorot dipanggil pusat C dan dalam angka ia bertepatan dengan titik (0.0), tetapi hiperbola juga boleh dipindahkan dan pusatnya sepadan dengan titik koordinat lain C (H, K).

Pada angka atas, paksi x adalah paksi fokus hiperbola, kerana terdapat lampu sorot, tetapi anda juga boleh membina seseorang yang paksi fokus adalah paksi dan paksi.

Hyperbola adalah sebahagian daripada lengkung yang dikenali sebagai conical, Mereka dipanggil kerana mereka boleh diperolehi dari potongan kerucut dengan bahagian rata. Hiperbola diperolehi apabila bersilang kerucut dan pesawat, dengan syarat ia tidak melalui puncak kerucut dan sudut yang membentuk satah dengan paksi kon adalah kurang daripada yang membentuk dengan paksi generatrix sama.

Bersama -sama dengan perumpamaan, lilitan dan elips, conics diketahui sejak zaman dahulu. Ahli matematik Yunani Apollonius Perga (262-190 SM) menulis perjanjian geometri di mana dia terperinci sifatnya dan dia sendiri memberi mereka nama-nama yang mereka saling mengenali sehingga hari ini.

Ciri -ciri hiperbola

Ini adalah beberapa ciri yang paling luar biasa dari hiperbola:

Ia adalah lengkung rata, oleh itu sudah cukup untuk memberikan koordinat (x, y) dari setiap titik yang dimiliki olehnya.
Ia juga merupakan lengkung terbuka, tidak seperti lilitan atau elips.
Ia mempunyai dua cawangan yang disusun secara simetri.
Kedua -dua paksi menegak dan paksi mendatar boleh dianggap sebagai paksi simetri, tetapi paksi di mana lampu sorot dipanggil paksi fokus atau paksi utama.
Ia simetri berkenaan dengan pusatnya.
Hyperbola merentasi paksi fokus pada dua mata yang dipanggil Simpang, Itulah sebabnya paksi fokus kadang -kadang dipanggil paksi sebenar, sementara paksi lain dipanggil Paksi khayalan, Kerana ia tidak mempunyai persamaan dengan hiperbola.
Pusat hiperbola terletak di tengah -tengah antara titik yang disebut foci.
Ia dikaitkan dengan dua garis yang sangat khusus yang disebut asymptotes, yang merupakan garis yang menghampiri hiperbola, tetapi tanpa melintasi mereka, ketika nilai -nilai x e y sangat besar. Asymptotes bersilang di tengah -tengah hiperbola.

Boleh melayani anda: Fungsi overjective: definisi, sifat, contoh

Persamaan dan Formula

Persamaan Hiperbol dengan Pusat Dalam (0.0)

Bermula dari definisi yang diberikan pada mulanya:

$\left |d__P_1-d__P_2 \right |=constante$

Untuk pemalar positif ini, ia biasanya dipanggil 2a dan ia adalah jarak yang memisahkan simpul hiperbola, kemudian:

$\left |d__P_1-d__P_2 \right |=2a$

Sebaliknya, DP₁, Dp₂ dan 2c adalah sisi segitiga yang ditunjukkan dalam Rajah 1, dan oleh geometri asas, pengurangan kuadrat sisi mana -mana segitiga selalu kurang dari segi empat baki. Jadi:

Ke -4²< 4c²

Dan:

ke < c

Hasil ini akan berguna tidak lama lagi.

Sebagai jarak antara dua mata p₁(x₁,dan₁) Dan p₂(x₂,dan₂) adalah:

$d_12=\sqrt(x_2-x_1)^2+(y_2-y_1)^2$

Dengan menggantikan koordinat p (x, y), f₁(-C, 0) dan f₂(C, 0) Ia tetap:

$\left |d_P_1-d_P_2 \right |=\left |\sqrt(x+c)^2+(y-0)^2-\sqrt(x-c)^2+(y-0)^2 \right |=2a$

Yang bersamaan dengan:

$\sqrt(x+c)^2+(y-0)^2-\sqrt(x-c)^2+(y-0)^2=\pm 2a$

Square dalam kedua -dua ahli untuk menghapuskan akar dan menyusun semula istilah yang anda capai:

$\left (c^2-a^2 \right )x^2-a^2 y^2 =\left (c^2-a^2 \right )a^2$

Kepada kuantiti c² - ke², yang selalu menjadi jumlah positif kerana < c, se la denomina b², Oleh itu perkara di atas ditulis semula sebagai:

b²x² - ke²dan² = a² b²

Membahagikan semua istilah dengan² b², Ia adalah persamaan hiperbola yang berpusat pada (0.0) dengan paksi sebenar mendatar:

$\fracx^2a^^2-\fracy^2b^^2=1$

Dengan a dan b lebih besar daripada 0. Persamaan ini dipanggil Persamaan Canonical Hyerbola dan penyebut untuk² Ia selalu sesuai dengan pecahan positif.

Hyperbola berpusat pada (0.0) dan dengan paksi sebenar menegak mengambil bentuk:

$\fracy^^2a^2-\fracx^^2b^2=1$ Persimpangan hiperbola dengan paksi koordinat

Persimpangan hiperbola dengan paksi koordinat sedang dilakukan masing -masing y = 0 dan x = 0 dalam persamaan:

Untuk y = 0

x² /ke² = 1 ⇒ x² = a²

x = ± a

Hiperbola memotong ke paksi x dalam dua titik yang dipanggil simpang, yang koordinat masing -masing adalah: x = a y x = -a

Untuk x = 0

Ia diperolehi -dan² /b² = 1, yang tidak mempunyai penyelesaian sebenar dan mengikuti bahawa hiperbola tidak dipotong ke paksi menegak.

Persamaan Hyperbola dengan Pusat Dalam (H, K)

Jika pusat hiperbola berada di titik c (h, k), maka persamaan kanoniknya adalah:

$\frac\left (x-h \right )^2a^^2-\frac\left (y-k \right )^2b^^2=1$

Elemen Hiperbola

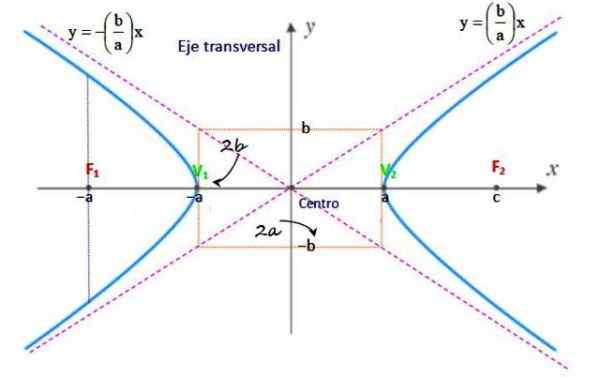Rajah 2. Elemen Hiperbola. Sumber: f. Zapata.

Pusat

Ia adalah titik tengah segmen f₁F₂Dan koordinatnya adalah (h, k) atau (x_{Sama ada},dan_{Sama ada}).

Boleh melayani anda: bahagian sintetik

Focos

Mereka adalah dua titik tetap f₁ dan f₂ yang berada di paksi sebenar hiperbola, berkenaan dengan perbezaan jarak ke titik p (x, y) tetap malar. Jarak antara lampu sorot dan pusat hiperbola adalah "c".

Radio Vektor

Ini dipanggil jarak antara titik p dan salah satu lampu sorot.

Jarak fokus

Ia adalah jarak yang memisahkan kedua -dua lampu sorot dan bersamaan dengan 2c.

Simpang

THE VERTICES v₁ dan v₂ Mereka adalah titik di mana hiperbola memotong paksi sebenar. Puncak dan pusat hiperbola dipisahkan oleh jarak a, oleh itu, jarak antara simpang adalah 2a.

Paksi fokus, paksi utama atau paksi sebenar

Ia adalah paksi di mana lampu sorot terletak dan mengukur 2c. Ia boleh ditempatkan di salah satu daripada dua paksi Cartesian dan hyperbola memotongnya pada titik -titik yang disebut simpang.

Paksi transversal, paksi sekunder atau paksi khayalan

Ia adalah paksi serenjang dengan paksi fokus dan langkah 2b. Hiperbola tidak bersilang, jadi ia juga dipanggil paksi khayalan.

Asymptotes

Mereka adalah dua baris, yang belum selesai ialah m₁ = (b/a) dan m₂ = - (b/a), yang dimaksudkan di tengah hiperbola. Lengkung tidak pernah memotong garis -garis ini dan produk antara jarak dari mana -mana titik hiperbola ke asymptotes, ia tetap.

Untuk mencari persamaan asymptotes, hanya sepadan dengan sebelah kiri persamaan kanonik hiperbola hingga 0. Sebagai contoh, untuk hiperbola berpusat pada asal:

$\fracx^^2a^2-\fracy^^2b^2=0\Rightarrow \fracy^^2b^2=\fracx^^2a^2$

Hyberbola Rectangle

Ia adalah segi empat tepat yang lebarnya adalah jarak antara simpang 2a dan jarak 2b dan memberi tumpuan kepada pusat hiperbola. Pembinaannya memudahkan susun atur manual hiperbola.

Sebelah lurus

Tali yang melalui salah satu lampu sorot, tegak lurus dengan paksi sebenar.

Eksentrik

Ia ditakrifkan sebagai kuota antara jarak fokus dan paksi sebenar:

E = c/a

Ia selalu lebih besar daripada 1, kerana c lebih besar daripada a, dan kurang dari √2.

Nilai dan menunjukkan sama ada hiperbola agak ditutup (segi empat tepat sempit, memanjang ke arah paksi utama) atau terbuka (segi empat tepat lebar, memanjang ke arah paksi khayalan).

Tangen lurus ke hiperbola pada titik p (x₁,dan₁)

Garis tangen ke hiperbola pada titik p (x₁,dan₁) Ia adalah bisektor dua vektor radio pada titik itu.

Untuk hiperbola dengan paksi utama selari dengan paksi x, cerun garis tangen ke hiperbola pada titik p (x₁,dan₁) diberikan oleh:

Boleh melayani anda: Operasi gabungan

$m=\left (\fracba \right )^2\left (\fracx_1y_1 \right )$

Dan jika hiperbola adalah paksi utama selari dengan paksi Y, maka:

$m=\left (\fracab \right )^2\left (\fracx_1y_1 \right )$

Contoh hiperbola

Penyebaran zarah alfa oleh nukleus

Dengan membombardir nukleus atom dengan zarah alfa, yang tidak lain hanyalah nukleus helium, ini ditolak, kerana mana -mana nukleus atom mempunyai caj positif. Nukleus helium ini tersebar berikutan trajektori hiperbola.

Trajektori badan sistem solar

Rajah 3: Planet Sistem Suria

Dalam sistem solar, objek bergerak di bawah tindakan daya graviti. Penerangan mengenai pergerakan itu berasal dari persamaan pembezaan di mana daya itu konservatif dan berkadar songsang dengan kuadrat jarak. Dan penyelesaian persamaan ini adalah kemungkinan trajektori yang mengikuti objek.

Nah, trajektori ini sentiasa konik: lilitan, elips, perumpamaan atau hiperbola. Dua yang pertama adalah lengkung tertutup, dan ini adalah bagaimana planet bergerak, tetapi beberapa komet masih terbuka trajektori, seperti perumpamaan atau hiperbola, dengan matahari terletak di salah satu lampu sorot.

Bunyi minimum

Apabila terdapat dua sumber bunyi, seperti dua penceramah yang memancarkan bunyi secara merata di semua arah, yang terletak di sepanjang garis lurus, minimum intensiti bunyi (gangguan merosakkan) berada di atas hiperbola yang paksi utamanya dikatakan garis, dan dalam lampu sorot Hyperbola adalah pembesar suara.

Latihan diselesaikan

Cari unsur -unsur hiperbola berikut: simpang, fokus dan asymptotes hiperbola dan membina grafnya:

$\fracx^^216-\fracy^^24=1$

Penyelesaian

Pusat hiperbola ini bertepatan dengan asal koordinat dan paksi sebenar adalah mendatar, kerana pecahan positif sepadan dengan pembolehubah x.

Hyperbola Semi -xes adalah:

ke² = 16 ⇒ a = 4

b² = 4 ⇒ b = 2

Dengan cara ini, segi empat tepat pusat mengukur 4 unit lebar dan 2 unit tinggi. Ingat bahawa ia disebutkan di atas bahawa c² - ke²= b², Jadi:

c² = a²+ b² ⇒ c² = 16 + 4 = 20

Oleh itu, separuh tugas fokus adalah:

C = √20 = 2√5

Dan fokus adalah pada titik koordinat f₁ (-2√5.0) dan f₂ (2√5.0).

Lereng asymptot adalah:

m = ± (b/a) = ± (2/4) = ± 0.5

Oleh itu persamaan masing -masing adalah:

dan₁ = 0.5x; dan₂ = -0.5x

Hyperbola boleh dengan mudah graf melalui perisian dalam talian seperti Geogebra:

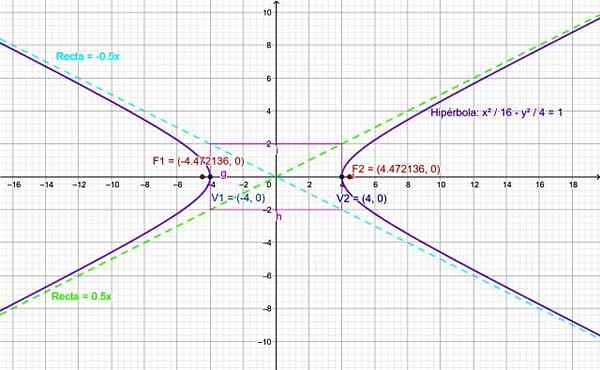Rajah 4. Graf untuk hiperbola latihan diselesaikan. Sumber: f. Zapata.

Rujukan