Matematik

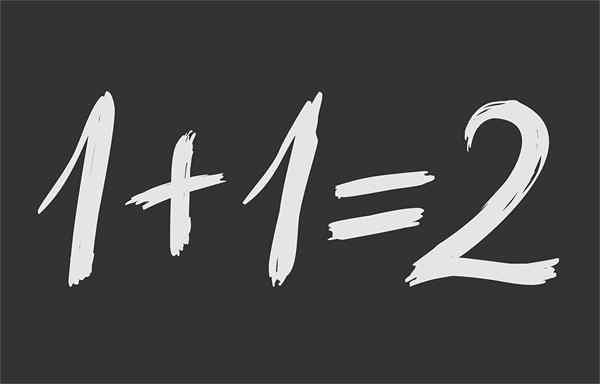
Kesamaan matematik

Kesamaan matematik
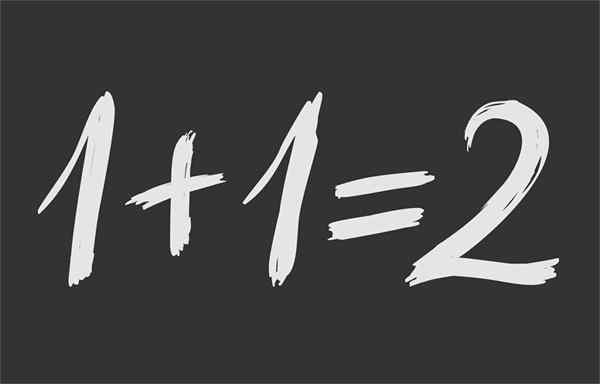Rajah 1.- Kesaksamaan matematik memastikan bahawa 1 + 1 adalah sama 2

Apakah kesamaan matematik?

Kesamaan matematik memastikan bahawa dua ungkapan adalah sama atau berbeza, mereka sama sekali setara. Ekspresi ini boleh menjadi pelbagai, contohnya nombor, huruf yang melambangkan jumlah atau magnitud, gabungan nombor dan huruf, matriks dan banyak lagi.

Simbol yang digunakan untuk menunjukkan kesamaan dalam bahasa matematik ialah dua garis selari dan mendatar, yang dalam teks bercetak adalah simbol yang terkenal "=". Sebagai contoh, jika anda mempunyai tiga epal, anda boleh menulis kesamaan berikut:

Bilangan epal = 3

Ungkapan "bilangan epal" adalah ahli kiri dan nombor 3 adalah ahli di sebelah kanan persamaan.

Seperti yang mungkin untuk menulis jumlah berangka dalam pelbagai cara, kesamaan digunakan untuk menunjukkannya. Mengambil kes tertentu untuk menggambarkan perkara itu, terdapat beberapa cara untuk menulis nombor 4, selain daripada yang paling jelas iaitu 4 = 4, yang berikut boleh ditulis, melalui kesamaan matematik:

2 + 2 = 4
6 - 2 = 4
8 ÷ 2 = 4
2 × 2 = 4
22 = 4

Kesaksamaan yang ditunjukkan di sini adalah benar, tetapi kesamaan mungkin tidak, contohnya 10 + 5 = 20 adalah palsu, kerana 10 + 5 = 15.

Pasti pembaca tahu cara lain untuk menulis nombor 4. Perhatikan bahawa ungkapan pada setiap sisi kesamaan boleh nombor, perkataan, huruf yang melambangkan jumlah atau simbol lain, sebagai contoh:

x + 1 = 7
ke2B - 1 = XY
f (x) = 2x2

Ahli matematik tidak selalu menggunakan simbol kesamaan, jadi perjanjian matematik lama sangat luas.

Ia dikaitkan dengan ahli matematik dan doktor Robert ingat (1510-1558), dilahirkan di Wales, penciptaan simbol kesamaan "=", begitu biasa dengan semua hari ini. Ingat, nampaknya bosan dengan menulis pada setiap masa frasa "sama seperti" dalam salah satu perjanjian matematiknya, dia memutuskan untuk menyingkat tempatnya dengan sanak sanak.

Boleh melayani anda: prisma pentagonal: ciri, bahagian, simpang, tepi, kelantangan

Sifat kesaksamaan matematik

Sifat berikut membolehkan berfungsi dengan betul dengan kesamaan matematik. Mereka adalah axiomatic, jadi mereka tidak memerlukan demonstrasi:

1.- Harta reflektif

Harta ini menetapkan bahawa jumlahnya sama dengan dirinya sendiri. Khususnya, kerana mana -mana nombor adalah sama dengan dirinya sendiri, yang sama boleh ditulis:

5 = 5

36.35 = 36.35

Sekiranya jumlahnya harfiah, atau gabungan huruf dan nombor, ia juga sama dengan dirinya sendiri:

3x = 3x

ke2BC-1 = a2BC-1

2.- Harta simetri

Jumlah atau ahli di kedua -dua belah persamaan boleh ditukar tanpa kesahihan yang hilang. Iaitu, jika apa yang ada di sebelah kiri "=" simbol ditulis di sebelah kanan anda, dan apa yang ada di sebelah kanan anda diletakkan di sebelah kiri, ia adalah persamaan yang sama.

Sebagai contoh, Ekspresi 5 + 2 = 7 bersamaan dengan yang satu ini: 7 = 5 + 2. Dengan cara yang sama:

12 + 8 = 20; 20 = 12 + 8

x + 1 = 3; 3 = x + 1

x - z = y; y = x - z

3.- Harta transitif

Harta ini merujuk kepada kesetaraan kesamaan. Jika dua kesamaan mempunyai ahli biasa, maka mereka juga sama, kerana secara umum:

Jika "x = y" dan "y = z" maka x = z

Untuk menggambarkan harta ini, pertimbangkan kedua -dua kesamaan berangka ini: 2 + 2 = 4 dan 6 - 2 = 4. Oleh kerana kedua -duanya adalah sama dengan 4 (mereka mempunyai ahli biasa), maka yang berikut dapat ditulis, tanpa kehilangan kesahihan:

2 + 2 = 6 - 2

Contoh lain, kali ini dengan huruf:

Ya x + 1 = 5

Dan

A - B = 5

Jadi:

x+1 = a - b

4.- Harta pembatalan

Kesamaan tidak diubah jika di kedua -dua ahli ada jumlah yang sama yang menambah (atau menolak) dan diputuskan untuk menghapuskan atau membatalkannya. Ini adalah harta pembatalan jumlah.

Ambil sebagai contoh kesamaan berangka berikut di mana 10 muncul di dalam anggota kanan dan di sebelah kiri:

Ia boleh melayani anda: Fungsi Trigonometrik: Asas, Dalam Plane Cartesian, Contoh, Latihan

2 + 2 + 10 = 6 - 2 + 10

Nombor 10 boleh dibatalkan tanpa kesamaan kehilangan kesahihannya, meninggalkan satu lagi kesamaan yang lebih pendek dan bersamaan dengan yang sebelumnya:

2 + 2 = 6 - 2

Dalam kesamaan (10 ÷ 2) - 3 = 5 - 3 Integer - 3 milik kedua -dua anggota kesamaan dan muncul sebagai penambahan, oleh itu boleh dibatalkan, mendapatkan:

10 ÷ 2 = 5

Ia juga berlaku dengan kuantiti literal, sebagai contoh:

Ya x + 2y + z = -a + b + z

Maka "z" boleh dibatalkan, kerana ia ditemui di kedua -dua belah persamaan sebagai menambah (dan dengan tanda yang sama).

Dengan berbuat demikian hasilnya:

x + 2y = -a + b

Ia juga boleh menentukan harta pembatalan pendaraban. Jika jumlah yang sama C mengadili kedua -dua ahli kesamaan, jumlah ini boleh dibatalkan, sebagai contoh:

Cx = cy

Kemudian C boleh dibatalkan untuk mendapatkan hanya:

x = y

5.- Harta Keseragaman

Kesaksamaan kekal tidak berubah dengan menambahkan, menolak, mengalikan atau membahagikan dengan kuantiti yang sama di kedua -dua belah yang sama.

Sebagai contoh, ia mempunyai 8 + 5 = 13, jika kedua -dua ahli melipatgandakan dengan nombor sewenang -wenangnya c = 2, kesamaan kekal:

(8+5) × 2 = 13 × 2

13 × 2 = 26

Kelas matematik yang sama

Terdapat pelbagai jenis kesamaan matematik, jadi mereka diklasifikasikan untuk pemahaman terbaik mereka dalam:

-Identiti, Mereka adalah kesamaan di mana kedua -dua ahli adalah sama:

2 = 2
x = x
2x = x + x

dan sebagainya.

-Persamaan, Ini adalah persamaan di mana satu atau lebih yang tidak diketahui muncul, dan benar untuk nilai -nilai tertentu, iaitu, kesamaan tidak dipenuhi untuk sebarang nilai sewenang -wenangnya, jadi mereka juga dikenali sebagai Kesamaan bersyarat. Contoh:

x + 1 = 5

x3 = 27

A + B = 40

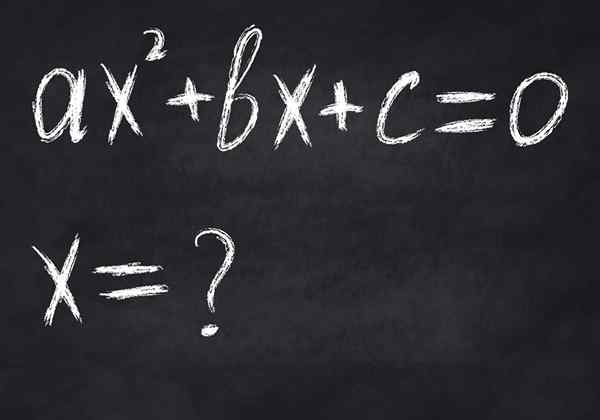Rajah 2.- Persamaan adalah kesamaan matematik bersyarat, kerana ia hanya dipenuhi untuk nilai pembolehubah tertentu. Imej menunjukkan persamaan darjah kedua, yang paling banyak mempunyai dua penyelesaian sebenar

-Kesamaan, Di dalamnya ahli kiri bersamaan dengan yang di sebelah kanan, walaupun mereka tidak sama, contohnya dalam: 23 = 8.

Boleh melayani anda: prinsip aditif

-Formula, Ia adalah kesamaan yang sentiasa dipenuhi untuk nilai -nilai pembolehubah bebas, seperti dalam formula yang terkenal untuk jarak d bergantung pada masa T mudah alih dengan pergerakan rectilinear seragam: D = v ∙ t

Latihan yang diselesaikan

Latihan 1

Tulis nombor 10 hingga empat kesamaan yang berbeza dan setara.

Penyelesaian

Semua kesamaan ini menyatakan nombor 10, tetapi dengan cara yang berbeza:

5 × 2 = 10

11-1 = 10

101= 10

20 ÷ 2 = 10

Latihan 2

Berapakah nilai x yang memenuhi kesamaan x + 1 = 3?

Penyelesaian

Kesamaan ini adalah persamaan, kerana nilai x tidak diketahui. Menggunakan harta 5, jika ungkapan x + 1 = 3 ditambah (-1) di kedua -dua belah simbol "=", kesamaan kekal:

x + 1 + (-1) = 3 + ( - 1)

Apabila menambah (-1) ke ahli kiri dan operasi diselesaikan, "x" bersendirian di sebelah kiri persamaan, prosedur ini dipanggil pelepasan:

x + 1 - 1 = 3-1

x = 2

Oleh itu, nilai yang memenuhi persamaan ini ialah x = 2.

Latihan 3

Sekiranya pergerakan rectilinear mudah alih mempunyai kelajuan 2.5 m/s, berapakah jarak yang berjalan selepas 3 saat?

Penyelesaian

Formula yang dilihat di bahagian sebelumnya digunakan, D = v ∙ t, di mana nilai v diganti:

D = 2.5 ∙ t

Ekspresi menjadi kesamaan apabila t = 3 saat dan operasi diselesaikan:

D = 2.5 ∙ 3 m = 7.5m

Yang menghasilkan kesamaan:

D = 7.5m

Rujukan

  1. Barnett, r. 2000. Pra-Sculpture. Ke -4. Edisi. McGraw Hill.
  2. Larson, r. 2012. Pra-Sculpture. Ke -8. Edisi. Pembelajaran Cengage.
  3. Pérez, v. Sifat kesamaan algebra. Pulih dari: matematik.Laguia2000.com.
  4. Sifat kesamaan. Diperolehi dari: PPS.K12.Atau.kita.
  5. Stewart, J. 2007. Pra-Kalkulasi: Matematik untuk Pengiraan. 5th. Edisi. Pembelajaran Cengage.