Formula/pekali induktansi bersama, aplikasi, latihan

The induktansi bersama menerangkan interaksi antara dua gegelung 1 dan 2 yang akan datang, yang mana arus berubah Yo Beredar melalui gegelung 1, menghasilkan aliran medan magnet yang berubah yang melintasi gegelung 2.

Aliran ini berkadar dengan arus dan pemalar berkadar adalah induktansi bersama₁₂. Menjadi φ_B2 Aliran medan magnet melalui gegelung 2, maka anda boleh menulis:

Φ_B2 = M₁₂ Yo₁

Rajah 1.- Transformer adalah penerapan utama induktansi bersama. Sumber: Pixnio.

Dan jika gegelung 2 mempunyai n₂ Laps:

N₂ . Φ_B2 = M₁₂ Yo₁

Dengan cara ini, pekali induktansi atau induktansi bersama₁₂ Antara kedua -dua gegelung adalah:

M₁₂ = N₂ . Φ_B2 / Yo₁

Induktansi bersama mempunyai unit Weber/Amperio atau WB/A, yang dipanggil Henry atau Henrio dan disingkat H. Oleh itu 1 Henry bersamaan dengan 1 wb/ a.

Nilai m₁₂ Ia bergantung pada geometri antara gegelung, bentuknya, saiz mereka, bilangan lilitan masing -masing dan jarak yang memisahkannya, serta kedudukan relatif di antara mereka.

[TOC]

Aplikasi induktansi bersama

Fenomena induktansi bersama mempunyai banyak aplikasi terima kasih kepada fakta bahawa asalnya adalah dalam undang-undang Faraday-Lenz, yang menyatakan bahawa arus yang berubah-ubah dalam litar mendorong arus dan voltan yang lain, tanpa memerlukan litar yang dihubungkan dengan kabel oleh kabel oleh kabel oleh kabel oleh kabel.

Apabila dua litar berinteraksi dengan cara ini dikatakan bahawa mereka digabungkan secara magnetik. Dengan cara ini, tenaga boleh pergi dari satu ke yang lain, suatu keadaan yang boleh digunakan dalam beberapa cara, seperti yang ditunjukkan oleh Nikola Tesla pada awal abad ke -20 (lihat Latihan Diselesaikan 1).

Dalam usahanya untuk menghantar elektrik tanpa kabel, Tesla berpengalaman dengan pelbagai peranti. Terima kasih kepada penemuannya, Transformer dicipta, peranti yang bergerak dari elektrik dari tumbuhan ke rumah dan industri.

Boleh melayani anda: vektor unit: ciri, bagaimana untuk mengeluarkannya, contohnya

Pengubah

Transformer menghantar voltan alternatif yang sangat tinggi di garisan elektrik, dengan itu meminimumkan kehilangan haba dan pada masa yang sama memberikan tenaga maksimum kepada pengguna.

Apabila voltan mencapai ini mesti dikurangkan, yang dicapai dengan pengubah. Ini terdiri daripada dua gegelung dawai yang dilancarkan di sekitar teras besi. Salah satu gegelung dengan n₁ giliran disambungkan ke voltan alternatif dan dipanggil utama. Yang lain, yang sekunder, mempunyai n₂ bertukar, menghubungkan ke perintang.

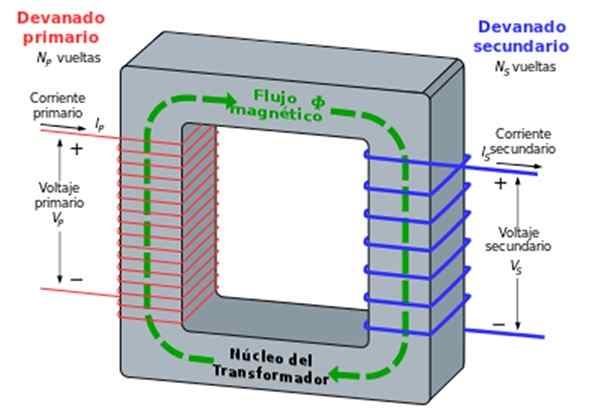Rajah 2. Pengubah. Sumber: Wikimedia Commons.

Teras besi memastikan bahawa semua garis medan magnet yang melewati gegelung juga berbuat demikian untuk yang lain.

Undang -undang Faraday menetapkan bahawa alasan antara voltan V₂ /V₁ (menengah /utama) adalah sama dengan sebab antara bilangan giliran n₂ /N₁:

V₂ /V₁ = N₂ /N₁

Menyesuaikan bilangan giliran dengan betul, voltan lebih besar atau kurang daripada pintu masuk diperolehi di pintu keluar.

Transformer dibina dari banyak saiz, dari transformer besar dalam pemasangan elektrik ke pemuat telefon bimbit, komputer riba, mp3 dan peranti elektronik lain.

Pacemaker

Kesan induktansi bersama juga terdapat di dalam pacemaker untuk mengekalkan kekerapan degupan jantung, sehingga dapat menjaga aliran darah stabil.

Pacemakers bekerja dengan bateri. Apabila mereka habis, gegelung luaran dapat menghantar kuasa ke gegelung lain di dalam alat pacu jantung. Oleh kerana prosedur dilakukan oleh induksi, tidak perlu mengemukakan pesakit kepada campur tangan baru apabila bateri habis.

Ia boleh melayani anda: lengkung penentukuran: Apa itu, bagaimana untuk melakukannya, contohnya

Pemuat tanpa wayar

Walaupun aplikasi biasa adalah pemuat tanpa wayar untuk objek yang berbeza seperti berus gigi dan telefon bimbit, yang merupakan peranti dengan penggunaan elektrik yang rendah.

Pada masa akan datang, penggunaan pemuat tanpa wayar untuk bateri kereta elektrik dinaikkan. Dan banyak penyelidikan hari ini bertujuan untuk menghasilkan elektrik tanpa wayar di rumah. Salah satu batasan utama untuk momen adalah jarak di mana arus dapat diinduksi terima kasih kepada medan magnet.

Latihan yang diselesaikan

- Latihan 1

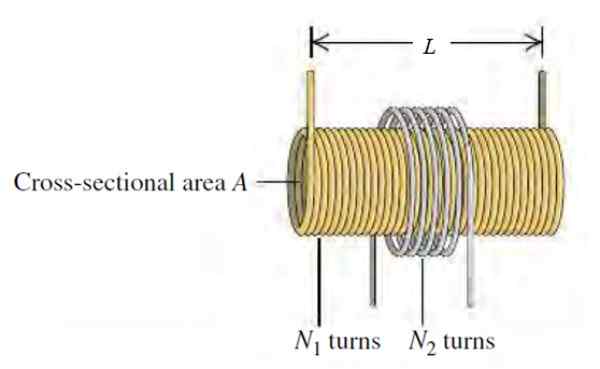
Dalam versi gegelung Tesla, digunakan sebagai penjana voltan tinggi dalam beberapa demonstrasi makmal, terdapat panjang L, Radio R, Radio R, Radio R, Radio R, Radio R, Radio R, Radio R, Radio R₁ dengan n₁ Panjang per unit panjang, dipasang secara bersatu dengan radiobin bulat r r bulat₂ dan n₂ pusingan.

Rajah 3. Skim gegelung Tesla. Sumber: Sears Zemansky. Fizik Universiti.

a) Cari induktansi bersama M litar, adakah ia bergantung pada arus yang beredar melalui solenoid?

b) Adakah induktansi bersama bergantung pada bentuk gegelung atau sama ada giliran anda lebih kurang digulung bersama?

Penyelesaian kepada

Besarnya medan magnet solenoid adalah berkadar dengan bilangan giliran dan arus yang beredar melaluinya, yang dilambangkan sebagai i₁, Oleh kerana solenoid adalah litar 1. Ia diberikan oleh ungkapan:

B₁ = μ_{Sama ada}N₁.Yo₁ / L

Aliran medan magnet yang solenoid mencipta dalam sira gegelung, yang merupakan litar 2, adalah hasil dari intensiti medan oleh kawasan yang dihubungkan dengan medan:

Φ_B2 = B₁. Ke₁

Kemana₁ Ia adalah kawasan bahagian silang solenoid dan bukan gegelung, kerana medan solenoid tidak sah di luarnya:

Ia dapat melayani anda: badan bercahaya: ciri -ciri dan bagaimana mereka menjana cahaya mereka sendiri

Ke₁ = π (r₁)²

Kami menggantikan kawasan dalam persamaan untuk φ_B2:

Φ_B2 = B₁. π (r₁)² = (μ_{Sama ada}N₁.Yo₁ / L). π (r₁)²

Dan induktansi bersama diberikan oleh:

M₁₂ = N₂ . Φ_B2 / Yo₁ = N₂. [(μ_{Sama ada}N₁.Yo₁ / L). π (r₁)² ] / Yo₁

M₁₂ = μ_{Sama ada} N₁ N₂ . π (r₁)² / L

Ia tidak bergantung pada arus yang beredar melalui solenoid, yang kita lihat bahawa ia dibatalkan.

Penyelesaian b

Seperti yang kita lihat, induktansi bersama tidak bergantung pada bentuk gegelung, atau sebagai stoking diketatkan. Satu -satunya pengaruh gegelung dalam induktansi bersama adalah bilangan giliran yang ada di dalamnya, iaitu n₂.

- Latihan 2

Dua gegelung sangat dekat antara satu sama lain dan salah satunya menjalankan arus pembolehubah pada masa yang diberikan oleh persamaan berikut:

I (t) = 5.00 e ^{-0.0250 t} Sen (377 t) a

Pada t = 0.800 saat Voltan yang diinduksi dalam gegelung kedua diukur, memperoleh -3.20 v. Cari induktansi bersama gegelung.

Penyelesaian

Kami menggunakan persamaan:

ε₂ = - m₁₂ (memberi₁/dt)

Untuk induktansi bersama di antara gegelung kita hanya menyebutnya m, kerana biasanya m₁₂ = M_{dua puluh satu}. Kami memerlukan derivatif pertama semasa berkenaan dengan masa:

memberi₁/dt =

= - 0.0250 x 5.00 e ^{-0.0250 t} X Sin (377 t) - 377 cos (377 t) x 5.00 e ^{-0.0250 t}  Ace

Kami menilai derivatif ini dalam t = 0.800 s:

memberi₁/dt = - 0.0250 x 5.00 e ^{-0.0250 x 0.800} x dosa (377 x 0.800) - 377 cos (377 x 0.800) x 5.00 e ^{-0.0250 x 0.800}  A/s =

= -5.00 e ^{-0.0250 x 0.800} [0.0250 x sen (377 x 0.800) + 377 cos (377 x 0.800)] =

= -1847.63 a/s

M = -3.20 v / -1847.63 a/s = 0.001732 h = 1.73 mh.

Rujukan

1. Figueroa, d. (2005). Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 6. Elektromagnetisme. Diedit oleh Douglas Figueroa (USB).
2. Hewitt, Paul. 2012. Sains Fizikal Konsep. 5th. Ed. Pearson.
3. Knight, r.  2017. Fizik untuk saintis dan kejuruteraan: Pendekatan Strategi. Pearson.
4. Sears, f. (2009). Fizik Universiti Vol. 2.
5. Serway, r., Jewett, J. (2008). Fizik untuk Sains dan Kejuruteraan. Jilid 2. Ke -7. Ed. Pembelajaran Cengage.