Matematik

Interpolasi linear

Kami menerangkan apakah intero linear, formulasnya, bagaimana untuk melakukan satu, dengan contoh dan latihan yang diselesaikan

Apakah interpolasi linear?

The Interpolasi linear Ia terdiri daripada menganggarkan lokasi titik dalam selang berangka, dengan mengandaikan bahawa nilai -nilai melampau selang dikatakan bersatu dengan garis. Dikenali persamaan garis ini, adalah mungkin untuk mencari titik yang tidak diketahui.

Idea ini disisipkan dalam angka berikut, yang menunjukkan pendekatan kepada graf fungsi antara titik a dan b. Dengan mengandaikan bahawa perkara -perkara ini adalah dekat, adalah mungkin untuk menghampiri lengkung yang menyatukan mereka melalui garis dan dengan itu mencari titik pertengahan.

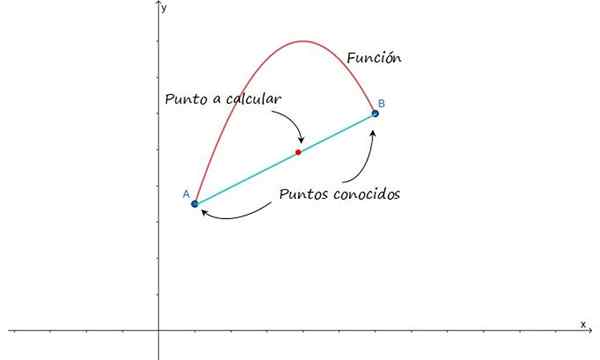Rajah 1.- Untuk membuat interpolasi linear antara titik a dan b, mesti diandaikan bahawa mereka bersatu dengan garis . Sumber: f. Zapata.

Anda juga boleh menghampiri lengkung yang bergabung dengan mata yang diberikan melalui fungsi kuadratik atau polinomial lain. Walau bagaimanapun, garis ini mempunyai kelebihan kesederhanaan matematiknya, jadi mudah dikendalikan, walaupun menjadi interpolasi yang paling mudah dari semua, mungkin hasilnya tidak tepat seperti yang diperoleh dengan menggunakan fungsi lain.

Formula

Terdapat dua titik koordinat [x_{Sama ada}, f (x_{Sama ada})] dan [x₁, f (x₁)] di antaranya ialah titik [x, g (x)], yang koordinatnya dikehendaki mengetahui.

Langkah pertama terdiri daripada menyertai titik yang diketahui melalui segmen garis, di mana koordinat titik kiraan dijumpai.

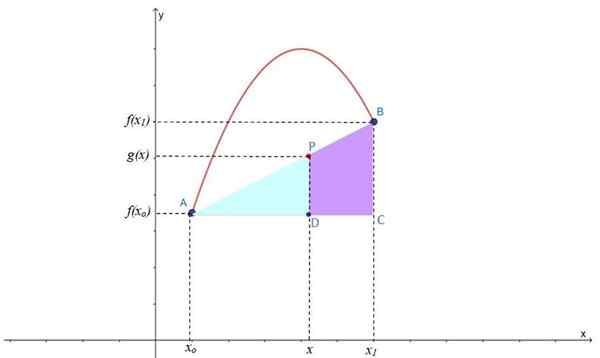Rajah 2.- Interpolasi linear untuk mencari titik P pada garis interpoching g (x), terletak di antara titik a dan b f (x). Sumber: f. Zapata.

Seperti yang anda lihat, dua segi empat tepat dibentuk: ABC dan APD, yang juga mempunyai sudut akut yang sama, jadi ia adalah segitiga yang sama, yang mana teorem Thales boleh digunakan:

Ia dapat melayani anda: geometri analisis

$\fracADAC=\fracAPAB=\fracPDBC$ Menggantikan ukuran segmen mengikut graf, hubungan berikut diperoleh:

$\fracx-x_ox_1-x_o=\fracg(x)-f(x_o)f(x_1)-f(x_o)$ Dari situ kita terus membersihkan g (x):

$g(x)=f(x_o)+\left [\fracf(x_1)-f(x_o)x_1-x_o \right ]\left ( x-x_o \right )$ Memanggil:

F₁(x₁) = y₁ ; F_{Sama ada}(x_{Sama ada}) = y_{Sama ada}; g (x) = y

Persamaan teratas berubah menjadi:

$y=y_o+\left [\fracy_1-y_ox_1-x_o \right ]\left (x-x_o \right )$

Julat ralat

Apabila fungsi menghampiri dengan kaedah ini, tahap ralat diberikan oleh nilai mutlak perbezaan antara fungsi f (x) dan garis interpolasi g (x):

Ralat = │f (x) - g (x) │

Cara membuat interpolasi linear?

Menjalankan interpolasi linear sangat mudah, anda hanya perlu mengikuti langkah -langkah ini:

Langkah 1

Tentukan titik yang tidak diketahui p (x, y).

Langkah 2

Mewujudkan dua titik yang mengehadkan selang di mana nilai yang akan dikira terletak, iaitu, mata (x x_{Sama ada},dan_{Sama ada}) dan (x₁, dan₁).

Langkah 3

Ganti semua nilai dalam persamaan:

$y=y_o+\left [\fracy_1-y_ox_1-x_o \right ]\left (x-x_o \right )$

Dan hitung hasilnya.

Contoh interpolasi linear

Contoh 1

Anda ingin mencari nilai anggaran LN 3 melalui interpolasi linear, memandangkan nilai berikut:

ln 2 = 0.693147 dan LN 4 = 1.386294

Bandingkan hasilnya dengan nilai LN 3 yang diperoleh melalui kalkulator dan tentukan margin yang dilakukan.

Langkah 1

Untuk mencari nilai anggaran LN 3, anda perlu meneruskan cara berikut: Pertama, yang tidak diketahui ditubuhkan, iaitu y = ln 3, bersebelahan dengan nilai yang sama dengan "x": x = 3. Inilah titik yang anda ingin hitung: (3, ln 3).

Langkah 2

Kemudian anda perlu menetapkan titik had selang dengan nilai yang diketahui. Ia diminta untuk berbuat demikian dengan beberapa mata seterusnya:

Had bawah: [x_{Sama ada} = 2; dan_{Sama ada} = ln 2 = 0.693147]
Had atas: [x₁ = 4; dan₁ = ln 4 = 1.386294]
Langkah 3

Nilai -nilai yang ditentukan dalam langkah 1 dan 2 digantikan dengan teliti dalam persamaan untuk menghasilkan hasil pendekatan kepada LN 3:

Boleh melayani anda: Berapa banyak penyelesaian yang dimiliki oleh persamaan kuadratik?

$y=y_o+\left [\fracy_1-y_ox_1-x_o \right ]\left (x-x_o \right )$

$ln\: 3= ln\: 2+\left [\fracln4-ln24-2 \right ]\left (3-2 \right )$
$ln\: 3= 0.693147+\left [\frac1.386294-0.6931474-2 \right ]\left (3-2 \right )=1.039721$ Nilai sebenar LN 3 yang diperolehi oleh kalkulator adalah:

ln 3 = 1.098612

Dan margin kesilapan adalah:

Ralat = │1.098612 - 1.03971 │ = 0.059

Kesalahan peratusan interpolasi dikira dengan membahagikan kesilapan antara nilai sebenar LN3 dan mendarabkan sebanyak 100 %:

Kesalahan peratusan = (ralat/nilai sebenar) × 100 = (0.059/1.098612) × 100% = 5.4%

Contoh 2

Sekarang anda ingin mencari nilai anggaran LN 3 dengan interpolasi linear, yang diketahui kedua -dua nilai ini:

Ln 2.5 = 0.916291 dan ln 3.5 = 1.252763

Juga menentukan kesilapan yang sepadan dan bandingkan dengan hasil contoh sebelumnya.

Langkah 1

Sekali lagi titik yang tidak diketahui ialah:

y = ln 3, x = 3

Langkah 2
Had bawah: [x_{Sama ada} = 2.5; dan_{Sama ada} = y_{Sama ada} = ln 2.5 = 0.916291]
Had atas: [x₁ = 3.5; dan₁ = ln 3.5 = 1.252763]
Langkah 3

$y=y_o+\left [\fracy_1-y_ox_1-x_o \right ]\left (x-x_o \right )$

$ln\: 3= ln \: 2.5+\left [\fracln\: 3.5-ln \: 2.53.5-2.5 \right ]\left (3-2.5 \right )=1.084527$ Memeriksa nilai yang ditawarkan oleh kalkulator:

ln 3 = 1.098612

Tahap ralat ditentukan dalam kes ini, yang menghasilkan:

Ralat = │1.098612 - 1.084527 │ = 0.014

Kesalahan peratusan dalam kes ini ialah ≈ 1.3 %. Berbanding dengan tahap ralat Contoh 1, nilai baru lebih tepat, kerana selang yang dipilih untuk interpolar lebih rendah.

Latihan yang diselesaikan

Latihan 1

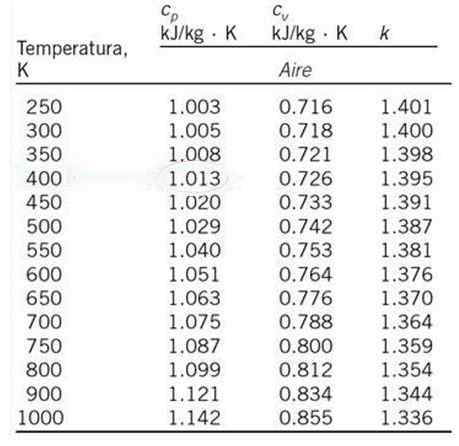
Hitung, dengan interpolasi linear, haba tertentu udara pada tekanan malar c_p dan suhu 530 K, bermula dari jadual nilai yang ditunjukkan di bawah.

Penyelesaian

Dalam resolusi banyak masalah, adalah perkara biasa bahawa nilai yang dicari tidak muncul tepat seperti yang dikehendaki dalam jadual nilai di tangan. Alternatif adalah memilih nilai yang paling dekat dengan yang dikehendaki, tetapi banyak kali interpolasi linear cukup untuk mencari pendekatan yang lebih baik.

Boleh melayani anda: tanda -tanda kumpulan

Nilai c_p 530 K tidak muncul dalam jadual yang dilampirkan, tetapi interpolasi linear boleh dibuat dengan pemanasan spesifik masing -masing pada 500 K dan 550 K, yang merupakan suhu yang paling dekat dengan 530 K dan pemanasan spesifiknya muncul dalam jadual yang ditunjukkan.

Haba haba spesifik masing -masing untuk suhu ini adalah:

T_{Sama ada} = 500 k; c_PO = 1.029 kJ /kg ∙ k

T₁ = 550 k; c_P1 = 1.040 kJ /kg ∙ k

Dan yang tidak diketahui adalah titik (500k, c_p)

Menggantikan formula interpolasi linear yang diberikan di atas, dengan T di tempat pembolehubah "x" dan c_p Daripada "Y", anda mempunyai:

$y=y_o+\left [\fracy_1-y_ox_1-x_o \right ]\left (x-x_o \right )$

$c_p= c_po+\left [\fracc_p1-c_poT_1-T_o \right ]\left (T-T_o \right )$

$c_p= 1.029+\left [\frac1.040-1.029550-500 \right ]\left (530-500 \right )\frackJkg\cdot K=1.03536\frackJkg\cdot K$

Latihan 2

Beban yang digunakan pada musim bunga (di Kilopondios) menghasilkan pemanjangan berikut (dalam milimeter) mengikut jadual yang ditunjukkan:

Kirakan pemanjangan apabila beban adalah 12.6 kp.

Penyelesaian

Biarkan dan nilai pemanjangan yang dicari apabila beban adalah c = 12.6 kp. Titik yang tidak diketahui ialah (12.6, y), yang merupakan antara mata:

C_{Sama ada} = 10 kp; dan_{Sama ada} = 105 mm

C₁ = 15 kp; dan₁ = 172 mm

Ia hanya tetap menggantikan nilai dalam persamaan:

$C= 105+\left [\frac172-10515-10 \right ]\left (12.6-10 \right )\: mm=139.84\: mm$ Latihan yang dicadangkan

Kirakan haba haba tertentu ke isipadu malar untuk suhu 727 K, menggunakan interpolasi linear dan jadual sekuriti latihan diselesaikan 1.

Rujukan

Akademi Rafa Vilchez. Cara melakukan interpolasi linear. Pulih dari: Academiraafavilchez.com
Chapra, s. 2007. Kaedah berangka untuk jurutera. 5th. Edisi. McGraw Hill.
Akademi Khan. Matematik interpolasi linear. Pulih dari: Khanacademy.org.
Kehidupan pendidikan. Formula Interpolasi Linear. Pulih dari: theeducationlife.com
X-Engineer. Interpolasi linear dan ekstrapolasi dengan kalkulator. Pulih dari: X-Engineer.org.

Interpolasi linear

Apakah interpolasi linear?

Formula

Julat ralat