Penjelasan undang -undang coulomb, formula dan unit, latihan, eksperimen

The Undang -undang Coulomb Adalah undang -undang fizikal yang mengawal interaksi antara objek yang dimuatkan secara elektrik. Ia dinyatakan oleh saintis Perancis Charles Augustin de Coulomb (1736-1806), terima kasih kepada hasil eksperimennya melalui keseimbangan kilasan.

Pada tahun 1785, Coulomb mengalami banyak masa dengan sfera elektrik kecil, contohnya membawa atau menjauhkan dua sfera, mengubah magnitud bebannya dan juga tandanya. Sentiasa menonton dan mendaftar dengan teliti setiap jawapan.

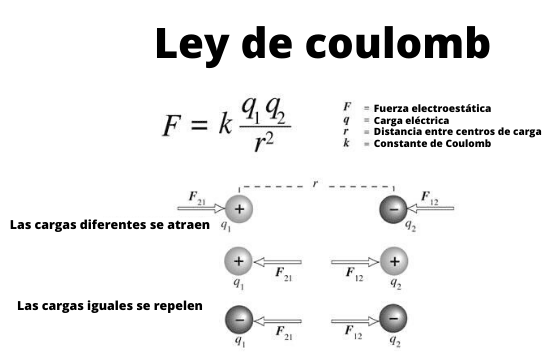
Rajah 1. Skim yang menunjukkan interaksi antara caj elektrik tertentu melalui undang -undang Coulomb.

Lingkaran kecil ini boleh dianggap sebagai Beban tertentu, iaitu objek yang dimensinya tidak penting. Dan mereka memenuhi, seperti yang diketahui sejak zaman orang Yunani kuno, bahawa banyak tanda yang sama ditolak dan tanda -tanda yang berbeza tertarik.

Rajah 2. Jurutera Tentera Charles Coulomb (1736-1806) dianggap sebagai ahli fizik yang paling penting di Perancis. Sumber: Wikipedia Commons.

Dengan ini, Charles Coulomb menemui perkara berikut:

-Daya tarikan atau penolakan antara dua caj tertentu adalah berkadar terus dengan produk magnitud beban.

-Kekuatan ini selalu diarahkan di sepanjang garis yang bergabung dengan beban.

-Akhirnya, magnitud daya berkadar songsang dengan kuadrat jarak yang memisahkan beban.

[TOC]

Formula dan Unit Undang -undang Coulomb

Terima kasih kepada pemerhatian ini, Coulomb menyimpulkan bahawa magnitud daya F Antara dua caj tertentu q₁ dan q₂, dipisahkan jarak r, Ia diberikan secara matematik sebagai:

Oleh kerana daya adalah magnitud vektor, untuk menyatakannya, vektor unit ditakrifkan sepenuhnya r Ke arah garis yang bergabung dengan beban (vektor unit mempunyai magnitud sama dengan 1).

Di samping itu, pemalar perkadaran yang diperlukan mengubah ungkapan sebelumnya ke dalam kesamaan dipanggil k_dan atau hanya k: The pemalar elektrostatik Sama ada Coulomb tetap.

Akhirnya, undang -undang Coulomb untuk beban tepat pada masanya ditubuhkan, diberikan oleh:

Kekuatan, seperti biasa dalam sistem unit antarabangsa, datang di Newton (N). Bagi caj, unit itu dipanggil Coulomb (c) untuk menghormati Charles Coulomb dan akhirnya jarak r datang dalam meter (m).

Secara hati memerhatikan persamaan sebelumnya, jelas bahawa pemalar elektrostatik mesti mempunyai unit n.m² / C², Untuk mendapatkan Newton sebagai hasilnya. Nilai pemalar ditentukan secara eksperimen sebagai:

Boleh melayani anda: vektor percuma: sifat, contoh, latihan

k_dan = 8.89 x 10 ⁹ N.m² / C² ≈ 9 x 10 ⁹ N.m² / C²

Rajah 1 menggambarkan interaksi antara dua caj elektrik: apabila mereka adalah tanda yang sama mereka ditolak, jika tidak, mereka menarik.

Perhatikan bahawa undang -undang Coulomb sesuai dengan undang -undang ketiga atau undang -undang tindakan dan tindak balas Newton, oleh itu magnitud F₁ dan F₂ Mereka sama, alamatnya sama, tetapi deria bertentangan.

Cara Memohon Undang -undang Coulomb

Untuk menyelesaikan interaksi antara caj elektrik, perkara berikut mesti diambil kira:

- Persamaan digunakan secara eksklusif dalam kes beban tertentu, iaitu, objek yang dimuatkan secara elektrik tetapi dimensi yang sangat kecil. Sekiranya objek yang dimuat mempunyai dimensi yang boleh diukur, perlu membahagikannya ke dalam beban yang sangat kecil dan kemudian tambahkan sumbangan setiap beban ini, yang mana pengiraan komprehensif diperlukan.

- Daya elektrik adalah magnitud vektor. Sekiranya terdapat lebih daripada dua caj berinteraksi, daya bersih pada beban q_Yo Ia diberikan oleh prinsip superposisi:

F_Jaring = F_i1 + F_I2 + F_i3 + F_i4 +... = Σ F_IJ

Di mana subskrip J Vale 1, 2, 3, 4 ... dan mewakili setiap beban yang tinggal.

- Mesti selalu konsisten dengan unit. Yang paling kerap bekerja dengan pemalar elektrostatik dalam unit jika, maka anda perlu memastikan beban berada di coulomb dan jarak dalam meter.

- Akhirnya, persamaan digunakan apabila beban berada dalam keseimbangan statik.

Latihan yang diselesaikan

- Latihan 1

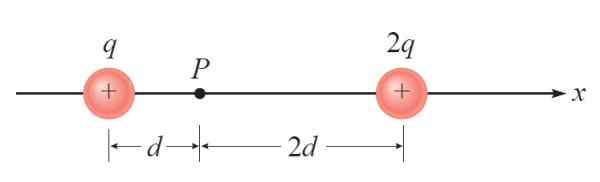
Dalam angka berikut terdapat dua beban tertentu +Q dan +2q. Beban tepat waktu ketiga --Q diletakkan pada p. Diminta untuk mencari kekuatan elektrik pada beban ini kerana kehadiran yang lain.

Rajah 3. Rajah untuk tahun diselesaikan 1. Sumber: Giambattista, a. Fizik.

Penyelesaian

Perkara pertama adalah untuk menubuhkan sistem rujukan yang sesuai, yang dalam kes ini adalah paksi mendatar atau x -axis. Asal sistem ini mungkin di mana sahaja, tetapi dengan keselesaan ia akan diletakkan di P, seperti yang ditunjukkan dalam Rajah 4A:

Boleh melayani anda: Bethelgeuse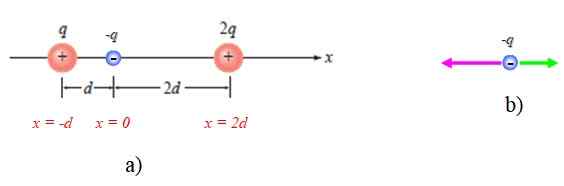Rajah 4. Skim untuk tahun diselesaikan 1. Sumber: Giambattista, a. Fizik.

Skim kekuatan pada -q juga ditunjukkan, dengan mengambil kira bahawa ia tertarik kepada dua yang lain (Rajah 4b).

Mari kita hubungi F₁ Kepada daya yang menjalankan beban yang pada beban -Q, mereka diarahkan sepanjang paksi x dan mata dalam erti kata negatif, oleh itu:

Vektor unit ke arah paksi x adalah x Dengan aksen circumflex dalam persamaan. Ini adalah notasi biasa untuk vektor unit. Tanda kurang muncul kerana kekuatan F₁ titik dalam erti kata negatif paksi.

Analog dikira F₂:

Perhatikan bahawa besarnya F₂ Ia adalah separuh daripada F₁, Walaupun bebannya berganda. Untuk mencari kekuatan bersih, mereka akhirnya ditambah secara vektor F₁ dan F₂:

F_Jaring = (-k + k/2).(Q² /d²) (x) N = - (k/2).(Q² /d²) (x) N

- Latihan 2

Dua sfera polistirena dengan jisim yang sama m = 9.0 x 10^-8 kg mempunyai beban positif yang sama q dan digantung oleh benang sutera panjang l = 0.98 m. Sfera dipisahkan jarak d = 2 cm. Kirakan nilai.

Penyelesaian

Keadaan pernyataan diterangkan dalam Rajah 5a.

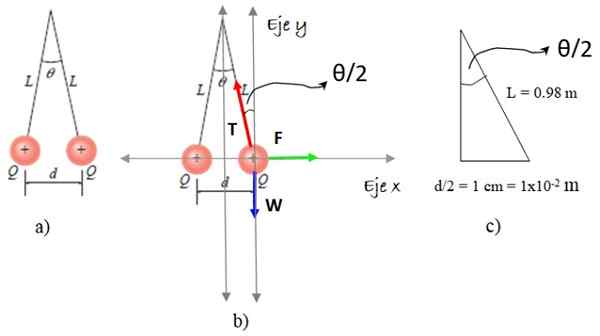Rajah 5. Skim untuk Resolusi Latihan 2. Sumber: Giambattista, a. Fizik /f. Zapata.

Kami memilih salah satu sfera dan di atasnya kami melukis gambarajah badan terpencil, yang merangkumi tiga daya: berat badan W, Ketegangan tali T dan penolakan elektrostatik F, Seperti yang muncul dalam Rajah 5b. Dan sekarang langkah -langkah:

Langkah 1

Nilai θ/2 dikira dengan segitiga Rajah 5c:

θ/2 = arcsen (1 x 10^-2/0.98) = 0.585º

Langkah 2

Maka anda harus memohon undang -undang kedua dan perlawanan Newton 0, kerana caj itu berada dalam baki statik. Penting untuk menyerlahkan ketegangan itu T Ia cenderung dan mempunyai dua komponen:

Σf_x = -T.dosa θ + f = 0

Σf_dan = T.cos θ - w = 0

Langkah 3

Kami membersihkan magnitud ketegangan persamaan terakhir:

Ia boleh melayani anda: Dinamik: Sejarah, Kajian, Undang -undang dan Teori Apa

T = w/ cos θ = mg/ cos θ

Langkah 4

Nilai ini digantikan dalam persamaan pertama untuk mencari magnitud f:

F = t sin θ = mg (sin θ / cos θ) = mg. Tg θ

Langkah 5

Seperti f = k q² /d², Ia membersihkan Q:

Dengan menggantikan nilai berangka yang disediakan oleh pernyataan, ia diperolehi:

Q = 2 × 10^-sebelas C.

Eksperimen

Memeriksa undang -undang Coulomb adalah mudah dengan menggunakan keseimbangan kilasan yang serupa dengan yang digunakan di makmalnya.

Terdapat dua sfera kecil Saúco, salah satunya, yang berada di tengah -tengah baki, digantung dari benang. Eksperimen ini terdiri daripada menyentuh sfera saúco yang dimuat turun dengan sfera logam lain yang dimuatkan dengan beban q.

Rajah 6. Keseimbangan kilasan Coulomb.

Segera beban diedarkan sama rata antara dua sfera Saúco, tetapi kemudian, seperti banyak tanda yang sama, mereka menolak. Daya yang menyebabkan kilasan benang dari benang dan segera bergerak dari sfera tetap bertindak pada sfera yang digantung.

Kemudian kita melihat bahawa ia berkisar beberapa kali sehingga keseimbangan mencapai. Kemudian kilasan bar atau benang yang memegangnya seimbang dengan daya penolakan elektrostatik.

Sekiranya sfera pada asalnya pada 0, sekarang sfera mudah alih akan menjadi sudut θ. Mengelilingi keseimbangan, terdapat pita siswazah dalam darjah untuk mengukur sudut ini. Apabila sebelum ini menentukan pemalar kilasan, maka daya penolakan dan nilai beban yang diperoleh oleh sfera Saúco mudah dikira.

Rujukan

1. Figueroa, d. 2005. Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 5. Elektrostatik. Diedit oleh Douglas Figueroa (USB).
2. GiMbattista, a. 2010. Fizik. Edisi kedua. McGraw Hill.
3. Giancoli, d.  2006. Fizik: Prinsip dengan aplikasi. 6th. Ed Prentice Hall.
4. Resnick, r. 1999. Fizikal. Vol. 2. Edisi ke -3. dalam bahasa Sepanyol. Syarikat Editorial Continental s.Ke. daripada c.V.
5. Sears, Zemansky. 2016. Fizik universiti dengan fizik moden. Ke -14. Ed. Jilid 2.