Undang -undang Formula, Unit, Eksperimen, Latihan, Faraday Formula,

The Undang -undang Faraday Dalam elektromagnetisme ia menetapkan bahawa aliran medan magnet yang berubah mampu mendorong arus elektrik dalam litar tertutup.

Pada tahun 1831, ahli fizik Inggeris Michael Faraday mengalami pemandu bergerak di dalam medan magnet dan juga medan magnet yang berbeza -beza yang melintasi pemandu tetap.

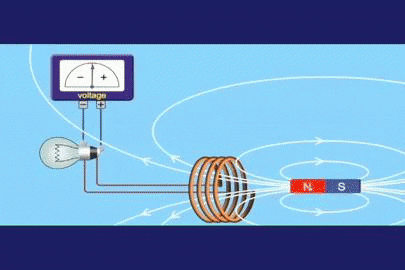Rajah 1. Eksperimen induksi Faraday

Faraday menyedari bahawa jika dia mengubah aliran medan magnet pada waktunya, dia dapat menubuhkan voltan berkadar dengan variasi tersebut. Jika ε adalah voltan atau daya elektromotor yang disebabkan (FEM yang disebabkan) dan φ adalah aliran medan magnet, dalam bentuk matematik ia dapat dinyatakan:

| ε | = Δφ/ΔT

Di mana simbol δ menunjukkan variasi kuantiti dan bar di FEM menunjukkan nilai mutlak ini. Oleh kerana ia adalah litar tertutup, arus boleh beredar dalam satu arah atau yang lain.

Fluks magnet, yang dihasilkan oleh medan magnet melalui permukaan, boleh berbeza -beza dalam pelbagai cara, sebagai contoh:

-Menggerakkan magnet bar melalui lingkaran bulat.

-Meningkatkan atau mengurangkan keamatan medan magnet yang melintasi gelung.

-Meninggalkan medan tetap, tetapi oleh beberapa mekanisme mengubah kawasan gelung.

-Menggabungkan kaedah di atas.

Rajah 2. Ahli fizik Inggeris Michael Faraday (1791-1867).

[TOC]

Formula dan unit

Katakan terdapat litar tertutup kawasan A, seperti lingkaran bulat atau pemberontakan yang sama dengan Rajah 1, dan terdapat magnet yang menghasilkan medan magnet B.

Aliran medan magnet φ adalah kuantiti skalar yang merujuk kepada jumlah garis medan yang menyeberangi kawasan a. Dalam Rajah 1 adalah garis putih yang meninggalkan tiang utara magnet dan kembali di selatan.

Boleh melayani anda: Kitaran Brayton: Proses, Kecekapan, Aplikasi, Latihan

Keamatan medan akan berkadar dengan bilangan garis per unit kawasan, jadi kita dapat melihat bahawa di tiang itu sangat sengit. Tetapi kita boleh mempunyai medan yang sangat sengit yang tidak menghasilkan aliran dalam gelung, yang dapat kita capai dengan mengubah orientasi ini (atau magnet).

Untuk mengambil kira faktor orientasi, aliran medan magnet ditakrifkan sebagai produk skalar antara B dan n, menjadi n Vektor unit biasa ke permukaan spase dan yang menunjukkan orientasinya:

Φ = B•n A = BA.cosθ

Di mana θ adalah sudut antara B dan n. Jika misalnya B dan n Mereka berserenjang, aliran medan magnet tidak sah, kerana dalam hal ini medan itu tangen ke satah spase dan tidak dapat menyeberangi permukaannya.

Sebaliknya B dan n Mereka selari, ini bermaksud bahawa medan itu berserenjang dengan satah sira dan garis -garisnya akan melalui maksimum.

Unit Sistem Antarabangsa untuk F ialah Weber (W), di mana 1 W = 1 t.m² (Membaca "Tesla per meter persegi").

Undang -undang Lenz 

Dalam Rajah 1 kita dapat melihat bahawa polariti perubahan voltan apabila magnet bergerak. Polariti ditubuhkan oleh undang -undang Lenz, yang menyatakan bahawa voltan yang diinduksi mesti menentang variasi yang menghasilkannya.

Jika, sebagai contoh, fluks magnet yang dihasilkan oleh magnet meningkat, pemandu menetapkan arus yang beredar mewujudkan alirannya sendiri, yang menentang peningkatan ini.

Jika, sebaliknya, aliran yang dihasilkan oleh magnet berkurangan, arus yang disebabkan beredar sedemikian.

Boleh melayani anda: skala termometrik

Untuk mengambil kira fenomena ini, tanda negatif kepada undang -undang Faraday diletakkan sebelum ini dan tidak lagi perlu untuk meletakkan bar nilai mutlak:

ε = -δφ/ΔT

Ini adalah undang-undang Faraday-Lenz. Jika variasi aliran adalah tak terhingga, delta digantikan dengan perbezaan:

ε = -dφ/dt

Persamaan sebelumnya sah untuk gelung. Tetapi jika kita mempunyai gegelung berputar, hasilnya jauh lebih baik, kerana fem berlipat ganda n kali:

ε = - n (dφ/dt)

Eksperimen Faraday

Untuk menghasilkan arus yang menyalakan mentol lampu, antara magnet dan lingkaran mesti ada pergerakan relatif. Ini adalah salah satu cara di mana aliran boleh berbeza -beza, kerana dengan cara ini intensiti medan yang melintasi perubahan gelung.

Pada masa ini pergerakan magnet terhenti, mentol keluar, walaupun magnet dibiarkan masih dalam spase. Apa yang diperlukan untuk mengedarkan arus ke mentol lampu ialah aliran medan berbeza -beza.

Apabila medan magnet berbeza dari masa ke masa, kita dapat menyatakannya sebagai:

B = B (T).

Dengan menjaga kawasan spase tetap dan meninggalkannya tetap pada sudut malar, yang dalam hal angka itu adalah 0º, maka:

 Untuk gelung Rajah 1 (cos 0º = 1):

Spase kawasan berubah -ubah

Sekiranya anda boleh menukar kawasan spase, meninggalkan penetapan orientasinya dan meletakkannya di tengah -tengah medan yang tetap, FEM yang diinduksi diberikan oleh:

Salah satu cara untuk mencapai matlamat ini adalah meletakkan bar yang meluncur di atas kereta api konduktif pada kelajuan tertentu, seperti yang ditunjukkan dalam angka berikut.

Boleh melayani anda: ío (satelit) Rajah 3. Penjana gelongsor. Sumber: Serway, r. Fizik untuk Sains dan Kejuruteraan.

Bar dan kereta api, ditambah mentol atau rintangan yang berkaitan dengan dawai pemandu, membentuk litar tertutup dalam bentuk spas segi empat tepat.

Semasa meluncur bar, panjangnya x meningkat atau berkurangan, dan dengan itu kawasan perubahan gelung, yang cukup untuk menghasilkan aliran berubah -ubah.

Variasi fluks magnet dengan putaran

Seperti yang kita katakan sebelumnya, jika sudut antara B Dan normal gelung berubah -ubah, aliran medan berubah mengikut:

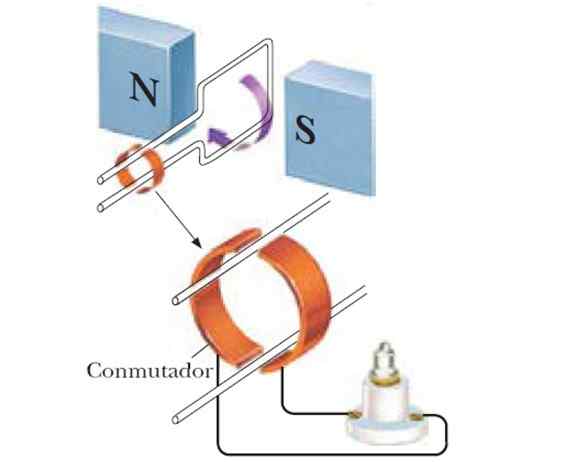Rajah 4. Sekiranya gelung diputar di antara tiang magnet, penjana sinusoid diperoleh. Sumber: f. Zapata.

Oleh itu, penjana sinusoidal diperoleh, dan jika satu gegelung digunakan, FEM yang diinduksi lebih besar:

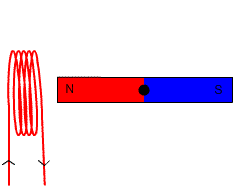Rajah 5. Dalam penjana ini, magnet diputar untuk mendorong arus dalam gegelung. Sumber: Wikimedia Commons.

Latihan diselesaikan

Gegelung bulat n pusingan dan radio r, bertukar Angular Ω di tengah -tengah medan magnet magnitud b. Cari ungkapan untuk FEM yang diinduksi maksimum dalam gegelung.

Penyelesaian

Ekspresi untuk FEM yang disebabkan oleh putaran digunakan apabila gegelung mempunyai pusingan n, mengetahui bahawa:

-Kawasan gegelung adalah a = πr²

-Sudut θ berbeza bergantung pada masa sebagai θ = ωt

Penting untuk mengambil kira bahawa θ = ωt pertama kali digantikan dalam undang -undang Faraday dan kemudian Ia berasal dari masa ke masa:

ε = -nba (cos θ) '= -nb (πr²).[cos (ωt)] '= nbΩ (πr²) Sen (ωt)

Oleh kerana FEM maksimum diminta, ini berlaku apabila sen ωt = 1, jadi akhirnya:

ε_maks = NbΩ (πr²)

Rujukan

1. Figueroa, d. 2005. Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 6. Elektromagnetisme. Diedit oleh Douglas Figueroa (USB).
2. GiMbattista, a. 2010. Fizik. Edisi kedua. McGraw Hill.
3. Giancoli, d.  2006. Fizik: Prinsip dengan aplikasi. 6th. Ed. Prentice Hall.
4. Resnick, r. 1999. Fizikal. Vol. 2. Edisi ke -3. dalam bahasa Sepanyol. Syarikat Editorial Continental s.Ke. daripada c.V.
5. Sears, Zemansky. 2016. Fizik universiti dengan fizik moden. Ke -14. Ed. Jilid 2.