Undang -undang Fick

Apa itu Undang -undang Fick?

The Undang -undang Fick Ia adalah persamaan matematik yang mengaitkan aliran jisim yang disebarkan dalam medium dengan kepekatan atau kecerunan tekanan. Ia dirumuskan pada tahun 1855 oleh ahli fisiologi Jerman dan doktor Adolf Fick, yang diilhamkan oleh undang -undang Fourier (pengaliran haba) dan ohm (pengaliran elektrik), memodelkan proses penyebaran oksigen ke alveoli paru -paru.

Undang -undang Fick membentangkan kekhususan bahawa ia bukan sahaja terpakai bagi fenomena penyebaran kimia atau biokimia, tetapi kepada apa -apa jenis alam semula jadi. Oleh itu, ia berfungsi untuk memodelkan penyebaran atom antara pepejal, yang sangat berguna dalam fizik bahan dan kejuruteraan.

Perwakilan proses penyebaran melalui membran semipermeable. Sumber: Gabriel Bolívar.

Walau bagaimanapun, pangkalan pusat adalah sama untuk hampir semua fenomena penyebaran, yang digambarkan di atas. Zarah ungu, menjadi atom atau molekul, tersebar melalui membran tebal tebal L dan kawasan melintang ke. Di sebelah kiri kita mempunyai kepekatan yang lebih besar c₁ zarah yang di sebelah kanan, c₂.

Undang -undang Fick menetapkan perkara berikut: aliran massa yang disebarkan melalui permukaan adalah berkadar dengan kecerunan kepekatan (c₂-C₁/L) dan pekali penyebaran atau diffusivity yang tetap d.

Undang -undang ini mempunyai dua bentuk: satu berdasarkan ruang (x), dan yang lain bergantung pada ruang dan waktu (x, t). Yang pertama digunakan untuk sistem dalam keadaan pegun, manakala yang kedua untuk sistem sebenar, bukan stationary.

Undang -undang pertama Fick

Komponen dan persamaan

Lebal L dari membran semipermeable mewakili jarak (x) bahawa zarah mesti bergerak untuk sampai ke sisi lain. Seperti yang dapat dilihat dalam imej, zarah ungu semakin banyak mereka berpindah dari petak kiri, di mana c₁ Ia hebat, kepekatannya berkurangan kepada nilai c₂. Iaitu, kepekatan berubah di sepanjang ketebalan membran, bergantung kepada x.

Variasi kepekatan ini bergantung pada jarak adalah apa yang dikenali sebagai kecerunan tumpuan: (c₂-C₁)/L o (c₂-C₁)/x. Perhatikan bahawa nilainya adalah negatif (-1), kerana c₂ > C₁.

Sebaliknya, kita juga mempunyai kelajuan yang zarah tersebar melalui membran atau ruang yang dipersoalkan. Kelajuan ini bergantung pada saiz dan jisim zarah, serta sifat persekitaran dan suhu. Pekali penyebaran d mewakili kelajuan ini, dan boleh tetap atau tidak semasa penyebaran.

Boleh melayani anda: penapis makmal): Ciri, fungsi, jenis

Dan akhirnya, kita mempunyai aliran jisim 'J' yang melintasi kawasan melintang membran atau saluran di mana zarahnya tersebar. Menggabungkan Terma ini, persamaan undang -undang pertama Fick dilahirkan:

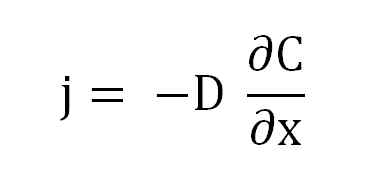Persamaan undang -undang pertama Fick. Sumber: Gabriel Bolívar.

Di mana j berkadar dengan d dan a (∂c/∂x), kecerunan tumpuan.

Tafsiran dan unit

Simbol negatif dalam persamaan berfungsi untuk meneutralkan tanda negatif kecerunan kepekatan. Jika tidak, J akan mempunyai nilai negatif, yang tidak diasingkan. Begitu juga, nilai d positif, sehingga dengan mengalikan dengan tanda negatif yang mendahuluinya, ia memberikan nilai negatif.

Undang -undang pertama Fick menunjukkan perkara berikut: semakin besar kecerunan tumpuan (∂c/∂x), semakin besar aliran jisim j. Iaitu perbezaan antara c₂ dan c₁ Ia menjadi lebih besar dan, oleh itu, lebih banyak zarah akan merebak melalui membran.

Sebaliknya, J juga bergantung kepada D, yang seterusnya bergantung kepada parameter seperti suhu, kelikatan, berat molekul, dan kawasan melintang ke:

D ∝ (a/l) (s/√m_W)

Di mana s adalah kelarutan zarah yang tersebar dengan alam sekitar, dan m_W Berat molekulnya.

Mengenai unit komponen atau syarat persamaan yang kita ada:

-C (kg · m^-3 atau mol · m^-3)

-D (m^-2· S^-1)

-J (kg · m^-2· S^-1 atau mol · m^-2· S^-1)

Anjakan kuadratik sederhana bersih

Semasa penyebaran zarah bertabrakan antara satu sama lain, dan selepas selang waktu yang singkat berakhir dengan jarak jauh Δx. Walau bagaimanapun, bergantung kepada makna anjakan ini, Δx boleh mempunyai nilai negatif atau positif (mengikut titik asal). Itulah sebabnya purata nilai Δx untuk semua molekul cenderung kepada 0.

Sebaliknya, nilai Δx sangat kecil berbanding dengan jarak yang menjalankan zarah. Apabila mereka bertembung, mereka kehilangan mobiliti ke arah arah, akibatnya mempunyai anjakan bersih yang terhad; Sebagai contoh, pendahuluan 2 cm dalam satu arah selepas perjalanan beratus -ratus meter dalam perlanggaran dan melantun.

Einstein pada tahun 1905 mendapati ungkapan matematik untuk tatal purata anjakan (oleh itu berbeza dari 0):

<(Δx)²> = 2dt

Menentukan

(Δx)_Rms ≡ <(Δx)²>^1/2 = (2dt)^1/2

(Δx)_Rms Ia adalah anjakan kuadratik bersih rata -rata zarah yang dipersoalkan. (Δx)_Rms Ia memberitahu kita berapa banyak zarah bergerak secara purata (dalam arah positif atau negatif) mengikut masa. Sesetengah zarah akan bergerak jauh atau jarak terdekat daripada (Δx)_Rms, menyebabkan pengedaran Gaussian.

Boleh melayani anda: kalsium oksida (CAO)

Undang -undang Kedua Fick

Persamaan

Undang -undang pertama Fick menerangkan penyebaran dalam keadaan pegun, iaitu, aliran jisim j tidak berubah dari masa ke masa. Walau bagaimanapun, dalam sistem sebenar, kita mempunyai keadaan bukan stasioner, di mana aliran jisim tidak hanya berbeza dalam ruang, tetapi juga dari masa ke masa. Oleh itu, ia berminat untuk menentukan (∂c/∂t).

Di bawah ini kita mempunyai dua persamaan yang mewakili undang -undang kedua Fick:

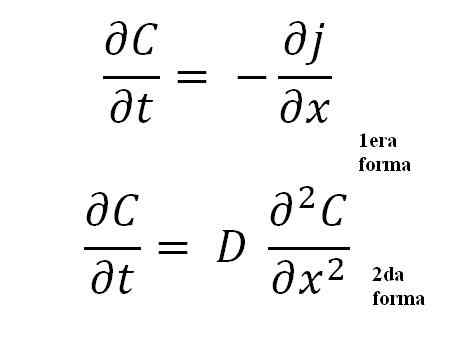Persamaan undang -undang kedua Fick. Sumber: Gabriel Bolívar.

Borang ke -2 adalah yang paling penting dari semua, kerana ia mewakili persamaan matematik umum untuk sebarang proses penyebaran; Sama ada haba, elektrik, atom, dll.

Potongan

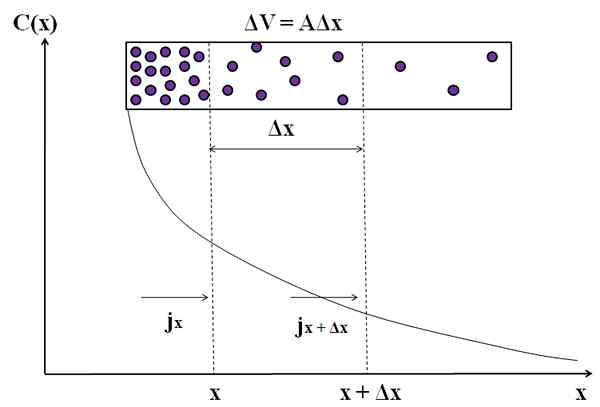Perwakilan grafik bagaimana aliran jisim tidak tetap dalam penyebaran molekul ini. Sumber: Gabriel Bolívar.

Pertimbangkan lagi zarah ungu dalam ruang segi empat tepat. Antara jarak x dan x+Δx kita mempunyai aliran j_x (masuk) dan j_x+Δx (keluar). Jumlah kamera antara jarak ini ditakrifkan oleh:

ΔV = aΔx

Perhatikan bahawa graf c (x) vs x tidak berasal dari garis lurus, jadi kami mempunyai nilai yang berbeza dari j (j_x ≠ j_x+Δx). Kita mesti menentukan ΔC/ΔT.

Jisim m_x Ia akan sama dengan:

m_x = J_x AΔT

Analisis dimensi membantu memahami mengapa:

kg = (kg · m^-2· S^-1) (m²) (S)

Dengan cara yang sama kita mengira m_x+Δx:

m_{x+ Δx} = J_x+Δx AΔT

Menjadi jisim yang terkumpul di rantau itu sama dengan Δm:

Δm = m_x - m_{x+ Δx}

= (j_x - J_{x+ Δx}) AΔt

= -(j_{x+ Δx} - J_x) AΔt

= -ΔJaΔT

Dan mengetahui bahawa ΔC = Δm/ΔV

ΔC = -ΔJAΔT/ ΔV

= -ΔJAΔT /AδX

= -ΔJΔT/ΔX

Kita jelaskan ΔC/ΔT

Δc/Δt = -ΔJ/Δx

Ungkapan ini menunjukkan bahawa variasi kepekatan dari masa ke masa adalah sama dengan variasi aliran j berkenaan dengan anjakannya. Memohon had untuk Δt dan Δx cenderung kepada 0 kita mendapat ungkapan yang sama sebagai derivatif separa:

∂c/∂t = -(∂j/∂x) (Borang 1)

Akhirnya, borang ke -2 diperoleh dengan menggantikan J dengan undang -undang pertama Fick:

∂c/∂t = -∂/∂x (-df/∂x)

= D (∂²C/∂x²) (Borang ke -2)

Latihan yang diselesaikan

Dalam latihan berikut, sistem yang sangat mudah akan dipertimbangkan yang tidak diketahui dapat diselesaikan dengan menggunakan undang -undang pertama Fick.

Latihan 1

Penyata

Dalam paip 15 meter panjang dan 21 sentimeter lebar, dan juga tepu dengan nitrogen, arus oksigen tersebar dari satu hujung ke yang lain pada suhu 0 ºC. Mengetahui bahawa tekanan di sebelah kiri (p₁) adalah 20 kg/m³, Dan tekanan di sebelah kanan (p₂) adalah 10 kg, tentukan:

Ia dapat melayani anda: ion hidronio

a) aliran massa yang tersebar

b) Berapa kilogram atau₂ Mereka akan merebak melalui paip dalam masa 17 minit?

c) kecerunan atau tekanan kepekatan

d) tekanan o₂ pada jarak 7 meter dari pintu masuk ke saluran paip

e) berapa 80 kg o₂ dalam menyebarkan paip ini?

Pertimbangkan bahawa d_O2-N2 sama dengan 1.8 · 10^-5 m²· S^-1.

Resolusi

Dari undang -undang pertama Fick kita perlu menyelesaikan subseksyen a):

J = -d (p₂-P₁)/L

= -(1.8 · 10^-5 m²· S^-1) (10-20) (kg/m³)/(15 m)

= 1.2 · 10^-5 kg · m^-2· S^-1

Ke b) kita memerlukan kawasan paip:

A = π (0.21 m)²

= 0.14 m²

Dan kami membiak j oleh a dan masa t untuk menentukan jisim atau₂ Dihidupkan:

m_O2 = (1.2 · 10^-5 kg · m^-2· S^-1) (17 s) (0.14 m²)

= 3.57 · 10^-5 kg

Sekarang, untuk subseksyen c) kita mempunyai kecerunan sama dengan:

Kecerunan = (p₂-P₁)/L

= (10-20) (kg/m³)/15 m

= -2/3 (kg/m³) · M^-1

Tetapi kita mengambil nilai positif, yang menjadikan akal fizikal:

2/3 (kg/m³) · M^-1

Nilai ini kemudiannya akan melayani kita untuk menyelesaikan subseksyen d) jika kecerunan ditafsirkan dengan baik: setiap meter tekanan atau₂ 2/3 kg/m akan jatuh³. Dengan menyebarkan 7 meter kita akan mempunyai:

2/3 (kg/m³) · M^-1 (7 m) = 14/3 atau 4.7 kg/m³

Iaitu, tekanan pada jarak itu akan:

(20-4.7) (kg/m³) = 15.3 kg/m³

Dan akhirnya, subseksyen e) adalah serupa dengan b), hanya kita sekarang yang jelas dan bukan jisim:

m_O2 = Jat

t = m_O2/Ja

= (80 kg)/(1.2 · 10^-5 kg · m^-2· S^-1) (0.14 m²)

= 47619.04 s atau 0.55 hari

Latihan 2

Penyata

Tentukan (Δx)_Rms Untuk sukrosa di dalam air pada t = 1 min, 1 jam dan 1 hari. Pekali penyebaran sukrosa di dalam air adalah 0.52 · 10^-5cm²· S^-1.

Resolusi

Kami menggunakan persamaan:

(Δx)_Rms ≡ <(Δx)²>^1/2 = (2dt)^1/2

Kami menilai (Δx)_Rms Dengan masa yang dinyatakan dalam beberapa saat. Untuk t = 1 min atau 60 s:

(Δx)_Rms = ((2 (0.52 · 10^-5cm²· S^-1) (60 -an))^1/2

= 0.025 cm

Untuk t = 1 h atau 3600 s:

(Δx)_Rms = ((2 (0.52 · 10^-5cm²· S^-1) (3600 -an))^1/2

= 0.19 cm

Dan akhirnya untuk t = 1 hari atau 86400 s:

(Δx)_Rms = ((2 (0.52 · 10^-5cm²· S^-1) (86400s))^1/2

= 0.95 cm

Perhatikan bahawa seiring berjalannya waktu dengan molekul sukrosa belum dapat bergerak 1 cm ke mana -mana arah.

Rujukan

1. Walter J. Moore. (1963). Kimia Fizikal. Dalam kinetik kimia. Edisi keempat, Longmans.
2. Iran. Levine. (2009). Prinsip Fizikokimia. Edisi keenam. MC Graw Hill.
3. Pengenalan kepada Sains dan Kejuruteraan Bahan. (11 Mac, 2018). Undang -undang Kedua Fick. Prof. Rajesh Prasad. [Video]. Pulih dari: youtube.com
4. Wikipedia. (2020). Undang -undang Penyebaran Fick. Diperoleh dari: dalam.Wikipedia.org
5. Laura Dickson. (10 September 2020). Penyebaran. Kimia Librettexts. Pulih dari: chem.Libretxts.org
6. Larissa Zhou et al. (1 September 2015). Memahami Teori Penyebaran dan Undang -undang Fick melalui Makanan dan Memasak. Persatuan Fisiologi Amerika. doi.org/10.1152/Advan.00133.2014