Matematik

Undang -undang De Morgan

Undang -undang De Morgan

Kami menerangkan apa undang -undang Morgan, kami menunjukkannya dan meletakkan contoh

Rajah 1.- Ahli matematik Augustus of Morgan (1806-1871) dan undang-undang logik cadangannya. Sumber: f. Zapata.

Apakah undang -undang De Morgan?

Undang-undang De Morgan adalah dua undang-undang logik milik logik proposisi yang dirumuskan oleh ahli matematik Inggeris Augustus of Morgan (1806-1871). Mereka menubuhkan perkara berikut, berkenaan dengan cadangan logik kompaun:

  1. Kebalikan dari konjungsi bersamaan dengan disjuncti.
  2. Penolakan disjuncti.

Dalam notasi logik cadangan, undang -undang De Morgan dinyatakan dengan cara yang padat dan lebih formal seperti ini:

  1. ~ (P ∧ q) ⇔ ~ p ∨q
  2. ~ (P ∨ q) ⇔ ~ p ∧q

Apa yang dinyatakan oleh undang -undang ini ialah, sama ada dalam penafian konjungsi atau disjuncti.

Untuk pemahaman yang lebih baik tentang undang -undang De Morgan, adalah perlu untuk mengkaji makna cadangan dan simbol yang digunakan dalam logik proposisi, untuk melihat bagaimana undang -undang ini mudah digunakan.

Notasi logik

Alat asas logik cadangan adalah cadangan. Cadangan logik adalah kenyataan yang mengakui a nilai sebenar, Sama ada benar atau palsu, tetapi tidak kedua -duanya pada masa yang sama. Dalam hal ini tidak ada kekaburan yang dibenarkan, iaitu, tidak ada keraguan.

Cadangan dilambangkan dengan huruf kecil, seperti dalam contoh berikut:

  • S: Mexico City adalah ibukota Mexico (benar).
  • S: Dengan menambah 2 dan 3, 4 (palsu) diperoleh.
  • J: Semua mamalia adalah haiwan darat (palsu).
Boleh melayani anda: heptagon

Terdapat juga cadangan yang lebih kompleks, yang disusun melalui penggunaan cadangan mudah, seperti ini:

  • S: Carlos akan pergi ke pawagam jika tidak hujan.
  • S: Ana adalah ahli biologi kimia atau marin.
  • A: Juan akan makan malam atau Pedro akan melihat permainan di televisyen.

Penyambung logik

Penyambung logik adalah simbol yang digunakan untuk menghubungkan cadangan mudah dan dengan itu membina cadangan yang lebih kompleks. Dalam logik cadangan masing -masing mempunyai makna tertentu.

Penyambung yang paling banyak digunakan adalah konjungsi, disjuncti.

Konjungsi

Konjungsi dilambangkan dengan huruf "v" terbalik. Cadangan komposit melalui konjungsi dilambangkan p ∧ q, seperti berikut:

  • P ∧ Q: Mexico City adalah ibukota Mexico dan berada di Amerika Utara.

Sangat mudah untuk mengenal pasti di sini bahawa p adalah "Mexico City adalah ibukota Mexico" dan Q adalah "di Amerika Utara".

Disjunction

Dua jenis disjunction dibezakan: yang lemah dan eksklusif. A disjungsi lemah Ia dilambangkan oleh ∨ dan dalam notasi logik ia akan menjadi p ∨ q. Contoh jenis disjunction ini adalah:

  • P ∨ Q: Juan adalah pemain bola sepak atau Juan adalah pemain tenis.

Sebaliknya, disjunction eksklusif Ia dilambangkan dengan tanda ⊻ dan menunjukkan bahawa salah satu cadangan mesti diketepikan, sebagai contoh:

P ⊻ Q: Alicia berumur 20 tahun atau Alicia berumur 22 tahun.

Perbezaan antara kedua -dua jenis adalah jelas, dalam disjuncti. Sebaliknya, dalam keadaan lemah, Juan mungkin pemain bola sepak dan tenis pada masa yang sama.

Penafian

Dengan meletakkan simbol ~ suatu cadangan, ini ditolak, seperti dalam:

  • Q: ~ (Veracruz adalah ibu kota Mexico).

Yang dibaca sebagai "Veracruz bukan ibu kota Mexico". Cara lain untuk menyatakan penafian, selain daripada "tidak", adalah melalui frasa seperti "palsu", "adalah satu pembohongan yang" dan "tidak benar bahawa".

Boleh melayani anda: interpolasi linear

Keadaan

Mereka adalah cadangan komposit yang biasanya menggunakan perkataan "ya" dan "kemudian ..." untuk menghubungkan dua proposisi di mana ada syarat atau implikasi. Bahagian proposisi yang ditulis sebaik sahaja "ya" adalah antecedent gelombang hipotesis cadangan dan apa yang berlaku selepas istilah "maka" adalah kesimpulan Sama ada akibatnya.

Simbol yang digunakan untuk keadaan adalah anak panah dari kiri ke kanan "→", oleh itu satu syarat antara dua proposisi diwakili sebagai p → q, yang boleh dibaca sebagai "jika p, kemudian q". Sebagai contoh:

P → Q: Sekiranya hujan pada waktu petang maka saya tidak akan bermain tenis.

Bi-conditionality

Dalam jenis proposisi ini frasa "ya, dan hanya jika" untuk menyambungkan dua cadangan, yang dipanggil ahli biconditional pertama dan kedua digunakan. Simbol yang digunakan adalah anak panah dua arah "↔".

Kedua -dua cadangan yang dihubungkan melalui "ya, dan hanya jika" dipanggil masing -masing Pertama dan ahli kedua dan bi-conditionity dua proposisi p dan q kekal sebagai p ↔ q. Sebagai contoh:

P ↔ Q: Maria suka menunggang basikal jika dan hanya jika hari itu cerah.

Demonstrasi undang -undang De Morgan

Undang -undang De Morgan adalah sebahagian daripada kesamaan logik dan boleh ditunjukkan melalui jadual kebenaran, yang digunakan untuk mengetahui nilai kebenaran (benar atau palsu).

Oleh kerana konjungsi hanya benar apabila p dan q benar, jadual kebenarannya adalah:

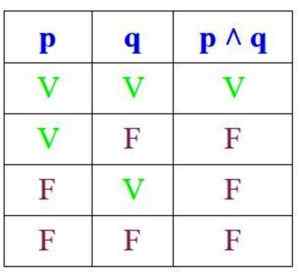
Sebaliknya, secara tidak sengaja, cadangan itu benar jika P dan Q adalah benar atau jika sekurang -kurangnya salah satu daripada mereka, tetapi ia adalah palsu jika kedua -duanya adalah:

Boleh melayani anda: permutasi tanpa pengulangan: formula, demonstrasi, latihan, contoh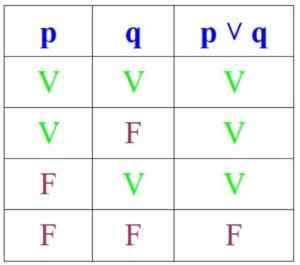

Sekarang, penafian mengubah kebenaran menjadi palsu dan sebaliknya. Dalam kes ini, nilai kebenaran ~ (p ∧ q) dan ~ (p ∨ q) adalah bertentangan dengan nilai kebenaran (p ∧ q) dan (p ∨ q):

Dan ia mesti disahkan bahawa keputusan ini diperolehi apabila menjalankan jadual kebenaran masing -masing (~ p ˅ ~ q) dan (~ p ˄ ~ q):

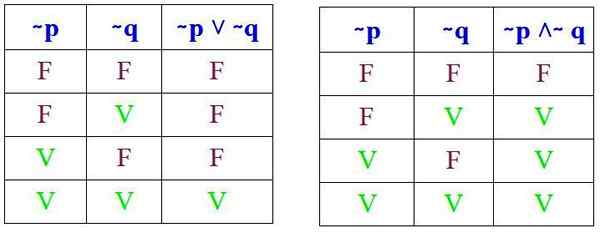
Dan sememangnya, apabila membandingkan jadual kebenaran masing -masing, diperhatikan bahawa undang -undang De Morgan dipenuhi. Sekarang dua contoh permohonannya akan dilihat.

Diselesaikan Contoh 1

Memohon undang -undang De Morgan untuk mencari ekspresi bersamaan: ~ (~ p ˅ ~ q)

  • Penyelesaian

Ekspresi yang diberikan dibandingkan ~ (~ p ˅ ~ q) dengan undang -undang Morgan:

~ (P ∨ q) ⇔ ~ p ∧q

Dan diperhatikan bahawa penafian itu sudah di luar kurungan dalam kedua -dua kes, oleh itu arahan undang -undang diikuti: ia menolak ~ P, menafikan ~ q dan penyambung diubah:

~ (~ P ˅ ~ q) ⇔ ~ (~ p) ∧ ~ (~ q) ⇔ p ∧ q

Diselesaikan Contoh 2

Tentukan ekspresi bersamaan ~ [~ p ˄ ~ (~ q)] ≡

  • Penyelesaian

Pertama, penafian ~ q dipermudahkan:

~ [~ P ˄ ~ (~ q)] ⇔ ~ [~ P ˄ Q]

Oleh kerana sudah ada penafian di luar pendakap, ungkapan yang dihasilkan dibandingkan dengan undang -undang Morgan: ~ (p ∧ q) ⇔ ~ p ∨q

Untuk menyelesaikan ~ [~ p ˄ q] anda harus menafikan ~ p, menafikan Q dan menukar penyambung:

~ [~ P ˄ q] ⇔ ~ (~ p) ∨ ~ q ⇔ p ˅ ~ q

Rujukan

  1. Becerra, j.M.  Nota Logik UNAM.
  2. Cemerlang. Dari undang -undang Morgan. Pulih dari: cemerlang.org.
  3. Tutorial Elektronik. Oleh teorem Morgan. Pulih dari: elektronik-tormales.WS.
  4. López, f. Pengenalan kepada logik matematik. Pulih dari: youtube.com
  5. Muñoz, c. Pengenalan kepada Logik. Diperolehi dari: Laman Web.UCM.adalah.