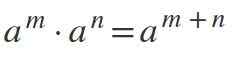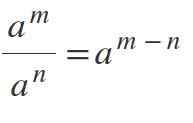Undang -undang eksponen

Apakah undang -undang eksponen?

The Undang -undang eksponen Mereka adalah orang -orang yang memohon kepada nombor yang menunjukkan berapa kali nombor asas mesti didarabkan dengan sendirinya. Eksponen juga dikenali sebagai kuasa. Potentiasi adalah operasi matematik yang dibentuk oleh asas (a), eksponen (m) dan kuasa (b), yang merupakan hasil operasi.

Eksponen biasanya digunakan apabila jumlah yang sangat besar digunakan, kerana ini tidak lebih daripada singkatan yang mewakili pendaraban bilangan yang sama dengan jumlah tertentu. Eksponen boleh positif dan negatif.

Apakah eksponen dalam operasi matematik?

Seperti yang dinyatakan di atas, eksponen adalah bentuk disingkat yang mewakili pendaraban nombor untuk diri mereka sendiri, di mana eksponen hanya berkaitan dengan nombor kiri. Sebagai contoh:

2³ = 2*2*2 = 8

Dalam hal ini nombor 2 adalah pangkalan kuasa, yang akan didarabkan 3 kali seperti yang ditunjukkan oleh eksponen, yang terletak di sudut kanan atas pangkalan. Terdapat pelbagai cara membaca ungkapan: 2 ditinggikan hingga 3 atau 2 yang dibangkitkan ke kiub.

Eksponen juga menunjukkan bilangan kali yang boleh dibahagikan, dan untuk membezakan operasi ini dari pendaraban yang eksponen membawa tanda tolak (-) di hadapannya (ia adalah negatif), yang bermaksud bahawa eksponen berada dalam penyebut penyebut pecahan. Sebagai contoh:

2^{- 4} = 1/2*2*2*2 = 1/16

Ini tidak boleh dikelirukan dengan kes di mana asasnya negatif, kerana ia bergantung kepada sama ada eksponen itu bahkan atau ganjil untuk menentukan sama ada kuasa itu positif atau negatif. Oleh itu, anda mesti:

- Sekiranya eksponennya, kuasa akan positif. Sebagai contoh:

(-7)² = -7 _* -7 = 49.

- Sekiranya eksponennya ganjil, kuasa akan negatif. Sebagai contoh:

(-2)⁵ = (-2)*(-2)*(-2)*(-2)*(-2) = -32.

Terdapat kes khas di mana jika eksponen sama dengan 0, kuasa adalah sama dengan 1. Terdapat juga kemungkinan bahawa asas adalah 0; Dalam hal ini, bergantung kepada eksponen, kuasa tidak dapat ditentukan atau tidak.

Untuk melaksanakan operasi matematik dengan eksponen yang diperlukan.

Apakah undang -undang eksponen?

Undang -undang pertama: kuasa eksponen sama dengan 1

Apabila eksponen adalah 1, hasilnya akan menjadi nilai yang sama seperti asas: a¹ = a.

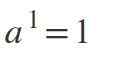
Contoh

9¹ = 9.

22¹ = 22.

895¹ = 895.

Undang -undang Kedua: Kekuatan Eksponen Sama dengan 0

Apabila eksponen adalah 0, jika asasnya berbeza dari sifar, hasilnya ialah: a⁰ = 1.

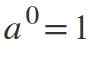
Contoh

1⁰ = 1.

323⁰= 1.

1095⁰ = 1.

Undang -undang Ketiga: Eksponen Negatif

Oleh kerana eksponen negatif, hasilnya akan menjadi pecahan, di mana kuasa akan menjadi penyebut. Sebagai contoh, jika m positif, maka^-m = 1/a^m.

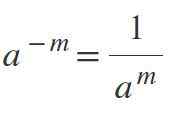
Contoh

- 3^-1 = 1/3.

- 6^-2 = 1/6² = 1/36.

- 8^-3 = 1/8³ = 1/512.

Undang -undang Keempat: pendaraban kuasa yang sama dengan yang sama

Untuk membiak kuasa di mana pangkalannya sama dan berbeza dari 0, pangkalannya dikekalkan dan eksponen ditambah: a^m _* keⁿ = a^m+n.    

Contoh

- 4⁴ _* 4³ = 4⁴⁺³ = 4⁷

- 8¹ _* 8⁴ = 8¹⁺⁴ = 8⁵

- 2² _* 2⁹ = 2²⁺⁹ = 2^sebelas

Undang -undang Kelima: Bahagian Kuasa Dengan Pangkalan Sama

Untuk membahagikan kuasa di mana pangkalannya sama dan berbeza dari 0, asasnya dikekalkan dan eksponen dikurangkan seperti berikut: a^m / keⁿ = a^M-N.    

Contoh

- 9² / 9¹ = 9 ^{(dua puluh satu)} = 9¹.

- 6^{lima belas} / 6¹⁰ = 6 ^{(15 - 10)} = 6⁵.

- 49¹² / 49⁶ = 49 ^{(12 - 6)} = 49⁶.

Undang -undang Keenam: Pendaraban kuasa yang berbeza dengan pangkalan yang berbeza

Dalam undang -undang ini terdapat kebalikan dari apa yang dinyatakan pada keempat; Iaitu, jika anda mempunyai pangkalan yang berbeza tetapi dengan eksponen yang sama, pangkalannya didarabkan dan eksponen dikekalkan: a^m _* b^m = (a_*b) ^m.

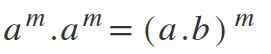
Contoh

- 10² _* dua puluh² = (10 _* dua puluh)² = 200².

- Empat lima^sebelas _* 9^sebelas = (45*9)^{11 =} 405^sebelas.

Cara lain untuk mewakili undang -undang ini adalah apabila pendaraban tinggi dengan kuasa. Oleh itu, eksponen akan dimiliki oleh setiap istilah: (a_*b)^m= a^m_* b^m.

Contoh

- (5_*8)⁴ = 5⁴ _* 8⁴ = 40⁴.

- (23 * 7)⁶ = 23⁶ _* 7⁶ = 161⁶.

Undang -undang Ketujuh: Bahagian Kuasa Berbeza

Sekiranya anda mempunyai pangkalan yang berbeza tetapi dengan eksponen yang sama, pangkalan dibahagikan dan eksponen dikekalkan:^m / b^m = (a / b)^m.

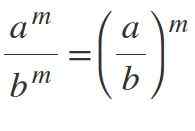
Contoh

- 30³ / 2³ = (30/2)³ = 15³.

- 440⁴ / 80⁴ = (440/80)⁴ = 5.5⁴.

Begitu juga, apabila suatu pembahagian tinggi dengan kuasa, eksponen akan dimiliki dalam setiap istilah: (a / b) ^m = a^m /b^m.

Contoh

- (8/4)⁸ = 8⁸ / 4⁸ = 2⁸.

- (25/5)² = 25² / 5² = 5².

Ada kes di mana eksponen negatif. Oleh itu, untuk menjadi positif, nilai pengangka dilaburkan dengan penyebut, seperti berikut:

- (A / b)^-n = (b / a)ⁿ = bⁿ / keⁿ.

- (4/5) ^-9 = (5/4) ⁹ = 5⁹ / 4⁴.

Undang -undang Kelapan: Kuasa Kekuatan

Apabila anda mempunyai kuasa yang dibangkitkan kepada kuasa lain -iaitu, dua eksponen pada masa yang sama -asasnya dikekalkan dan eksponennya berlipat ganda: (a^m)ⁿ= a^m*n.

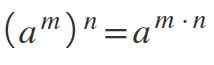
Contoh

- (8³)² = 8 ^(3*2) = 8⁶.

- (13⁹)³ = 13 ^(9*3) = 13²⁷.

- (238¹⁰)¹² = 238^{(10 * 12)} = 238¹²⁰.

Undang -undang kesembilan: eksponen pecahan

Jika kuasa mempunyai sebagai eksponen pecahan, ini diselesaikan dengan mengubahnya menjadi akar N-esima, di mana pengangka tetap sebagai eksponen dan penyebutnya mewakili indeks akar:

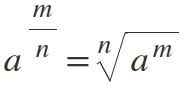
Contoh

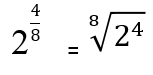
Latihan yang diselesaikan

Latihan 1

Kirakan operasi antara kuasa yang mempunyai pangkalan yang berbeza:

2⁴ _* 4⁴ / 8².

Penyelesaian

Memohon peraturan eksponen, pangkalannya didarabkan dalam pengangka dan eksponen dikekalkan, seperti ini:

2⁴ _* 4⁴ / 8²= (2_*4)⁴ / 8²  = 8⁴ / 8²

Sekarang, kerana terdapat pangkalan yang sama, tetapi dengan eksponen yang berbeza, asasnya dikekalkan dan eksponen dikurangkan:

 8⁴ / 8² = 8^{(4 - 2)} = 8²

Latihan 2

Kirakan operasi antara kuasa tinggi ke kuasa lain:

(3²)³ _* (2 _* 6⁵)^-2 _* (2²)³

Penyelesaian

Memohon undang -undang, anda mesti:

(3²)³ _* (2 _* 6⁵)^-2 _* (2²)³

= 3⁶ _* 2^-2 _* 2^-10 _* 2⁶

= 3⁶ _* 2^{(-2) + (- 10)} _* 2⁶

= 3⁶ _*  2^-12 _* 2⁶

= 3⁶ _* 2^{(-12) + (6)}

= 3⁶ _* 2⁶

= (3_*2)⁶

= 6⁶

= 46.656

Rujukan

1. Aponte, g. (1998). Asas Matematik Asas. Pendidikan Pearson.
2. Corbalán, f. (1997). Matematik digunakan untuk kehidupan seharian.
3. Jiménez, J. R. (2009). Matematik 1 Sep.
4. Max Peters, w. L. (1972). Algebra dan trigonometri.
5. Rees, ms. K. (1986). Reverte.