Algebra vektor

Apakah aljabar vektor?

Dia Algebra vektor Ia adalah cabang matematik yang bertanggungjawab mengkaji sistem persamaan linear, vektor, matriks, ruang vektor dan transformasi linear mereka. Ia berkaitan dengan bidang seperti kejuruteraan, resolusi persamaan pembezaan, analisis fungsional, penyelidikan operasi, grafik pengiraan, antara lain.

Satu lagi bidang yang diterima oleh algebra linear adalah fizik, kerana melalui ini, mungkin untuk membangunkan kajian fenomena fizikal, menggambarkan mereka melalui penggunaan vektor. Ini telah memungkinkan pemahaman yang lebih baik tentang alam semesta.

Asas

Algebra vektor berasal dari kajian quaternions (lanjutan nombor sebenar) 1, i, j, dan k, serta geometri Cartesian yang dipromosikan oleh Gibbs dan Heaviside, yang menyedari bahawa vektor akan berfungsi sebagai instrumen untuk mewakili mewakili beberapa fenomena fizikal.

Algebra vektor dikaji melalui tiga asas:

Geometri

Vektor diwakili oleh garis yang mempunyai orientasi, dan operasi seperti jumlah, penolakan dan pendaraban oleh nombor sebenar ditakrifkan melalui kaedah geometri.

Secara analitik

Penerangan tentang vektor dan operasi mereka dijalankan dengan nombor, yang dipanggil komponen. Penerangan jenis ini adalah hasil perwakilan geometri kerana sistem koordinat digunakan.

Axiomatically

Penerangan tentang vektor dibuat, tanpa mengira sistem koordinat atau apa -apa jenis perwakilan geometri.

Kajian angka dalam ruang dilakukan melalui perwakilannya dalam sistem rujukan, yang boleh dalam satu atau lebih dimensi. Antara sistem utama ialah:

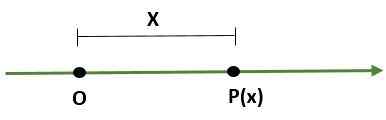
• Sistem unidimensional, bahawa ia adalah garis di mana titik (atau) mewakili asal dan titik lain (p) menentukan skala (panjang) dan arah ini:

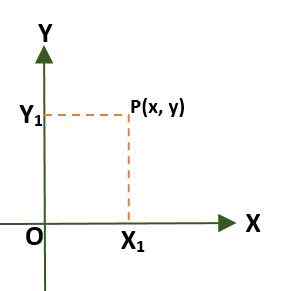
• Sistem koordinat segi empat tepat (dua dimensi), yang terdiri daripada dua garis tegak lurus yang dipanggil paksi x dan y, yang melewati satu titik (atau) asal; Dengan cara ini rancangan itu dibahagikan kepada empat wilayah yang dipanggil kuadran. Dalam kes ini, satu titik (p) dalam satah diberikan oleh jarak yang ada di antara paksi dan p.

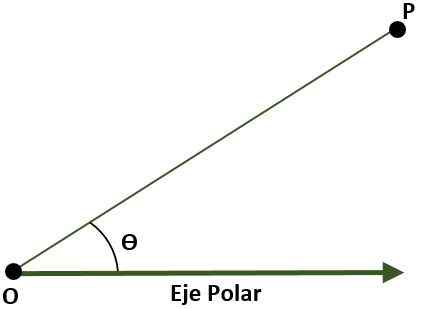
• Sistem koordinat kutub (dua dimensi). Dalam kes ini, sistem ini terdiri daripada titik o (asal) yang dipanggil tiang dan separuh rebus dengan asal atau dipanggil paksi kutub. Dalam kes ini, titik P satah, dengan merujuk kepada tiang dan paksi kutub, diberikan oleh sudut (ɵ), yang dibentuk oleh jarak antara asal dan titik p.

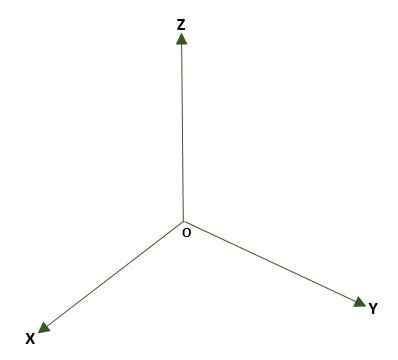
• Sistem tiga -dimensi segi empat tepat, Dibentuk oleh tiga garis tegak lurus (x, y, z) yang mempunyai titik atau di ruang angkasa. Tiga pesawat koordinat dibentuk: XY, XZ dan YZ; Ruang akan dibahagikan kepada lapan wilayah yang dipanggil oktan. Rujukan titik P ruang diberikan oleh jarak yang ada di antara pesawat dan p.

Magnitud

Besarnya adalah jumlah fizikal yang boleh dikira atau diukur melalui nilai berangka, seperti dalam hal beberapa fenomena fizikal; Walau bagaimanapun, sering kali perlu untuk menggambarkan fenomena ini dengan faktor lain yang tidak berangka. Itulah sebabnya magnitud diklasifikasikan kepada dua jenis:

Magnitud skalar

Mereka adalah jumlah yang ditakrifkan dan mewakili dengan cara berangka; iaitu, dengan modul bersama dengan unit ukuran. Sebagai contoh:

a) Masa: 5 saat.

b) Massa: 10 kg.

c) Jilid: 40 ml.

d) Suhu: 40 ºC.

Magnitud vektor

Mereka adalah jumlah yang ditakrifkan dan diwakili oleh modul bersama dengan unit, dan juga dengan rasa dan arah. Sebagai contoh:

Dapat melayani anda: simbolisasi ekspresi

a) Kelajuan: (5ȋ - 3 ĵ) m/s.

b) Pecutan: 13 m /s²; S 45º e.

c) Kekuatan: 280 N, 120º.

d) Berat: -40 ĵ kg -f.

Magnitud vektor diwakili secara grafik oleh vektor.

Apa itu vektor?

Vektor adalah perwakilan grafik magnitud vektor; iaitu, mereka adalah segmen garis di mana akhir terakhirnya adalah hujung anak panah.

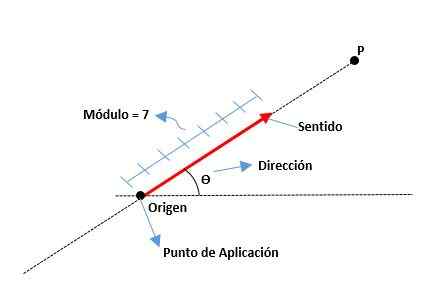
Ini ditentukan oleh modulnya atau panjang segmen, rasa mereka yang ditunjukkan oleh hujung anak panahnya dan arahnya mengikut garis yang dimiliki olehnya. Asal vektor juga dikenali sebagai titik permohonan.

Unsur -unsur vektor adalah seperti berikut:

Modul

Ia adalah jarak dari asal hingga akhir vektor, diwakili oleh nombor sebenar bersama dengan satu unit. Sebagai contoh:

| Om | = | A | = A = 6 cm

Alamat

Ia adalah ukuran sudut yang wujud antara paksi x (dari positif) dan vektor, serta titik kardinal (utara, selatan, timur dan barat) juga digunakan.

Rasa

Ia diberikan oleh hujung anak panah yang terletak di hujung vektor, yang menunjukkan di mana ini diarahkan.

Klasifikasi vektor

Umumnya, vektor diklasifikasikan sebagai:

Vektor tetap

Ia adalah orang yang permohonan (asal) ditetapkan; iaitu, ia tetap dikaitkan dengan ruang ruang, jadi ia tidak dapat bergerak dalam hal ini.

Vektor percuma

Ia boleh bergerak dengan bebas di angkasa kerana asalnya bergerak ke mana -mana titik tanpa mengubah modul, makna atau arahnya.

Vektor gelongsor

Ia adalah salah satu yang dapat memindahkan asalnya di sepanjang garis tindakannya tanpa mengubah modul, makna atau arahnya.

Sifat vektor

Antara sifat utama vektor adalah seperti berikut:

Melengkapkan vektor

Mereka adalah vektor percuma yang mempunyai modul yang sama, arah (atau ini selari) dan rasa sebagai vektor gelongsor atau vektor tetap.

Vektor setara

Ia berlaku apabila dua vektor mempunyai alamat yang sama (atau selari), pengertian yang sama, dan walaupun mempunyai modul dan titik aplikasi yang berbeza, mereka menyebabkan kesan yang sama.

Kesamaan vektor

Ini mempunyai modul, arah dan rasa yang sama, walaupun titik permulaan mereka berbeza, yang membolehkan vektor selari bergerak ke dirinya sendiri tanpa menjejaskannya.

Vektor bertentangan

Mereka adalah orang -orang yang mempunyai modul dan arah yang sama, tetapi maknanya bertentangan.

Vektor kesatuan

Ia adalah satu di mana modul sama dengan unit (1). Ini diperoleh dengan membahagikan vektor dengan modulnya dan digunakan untuk menentukan arah dan arah vektor, sama ada dalam satah atau di ruang angkasa, menggunakan asas piawai atau vektor unit, iaitu:

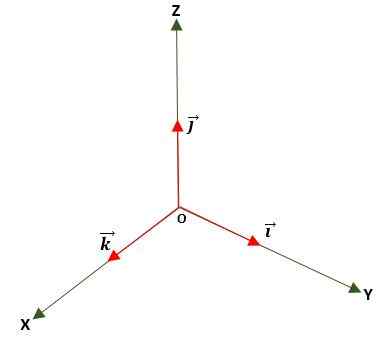
Vektor null

Ia adalah modul yang sama dengan 0; iaitu, titik asalnya dan melampau bertepatan pada titik yang sama.

Komponen vektor

Komponen vektor adalah nilai -nilai unjuran vektor pada paksi sistem rujukan; Bergantung pada penguraian vektor, yang boleh berada dalam paksi dua atau tiga dimensi, dua atau tiga komponen akan diperolehi.

Komponen vektor adalah nombor sebenar, yang boleh positif, negatif atau bahkan sifar (0).

Dengan cara ini, jika anda mempunyai vektor ā, yang berasal dari sistem koordinat segi empat tepat dalam satah xy (dua dimensi), unjuran pada paksi x adalah āx dan unjuran pada paksi y dan āy. Oleh itu, vektor akan dinyatakan sebagai jumlah vektor komponennya.

Contoh

Contoh pertama

Anda mempunyai vektor yang bermula dari asal dan koordinat hujungnya diberikan. Oleh itu, vektor ā = (ā_x; Ke_dan) = (4; 5) cm.

Boleh melayani anda: 120 pembahagi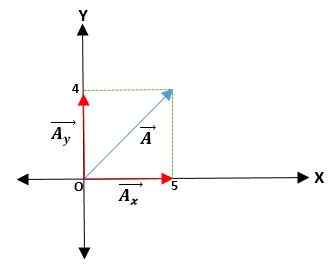

Jika vektor ā bertindak pada asal -usul sistem koordinat segi tiga tiga dimensi (di ruang angkasa) x, y, z, ke titik lain (p), unjuran pada paksi mereka akan menjadi āx, āy dan āz; Oleh itu, vektor akan dinyatakan sebagai jumlah tiga vektor komponennya.

Contoh kedua

Anda mempunyai vektor yang bermula dari asal dan koordinat hujungnya diberikan. Oleh itu, vektor ā = (a_x; Ke_dan; Ke_z) = (4; 6; -3) cm.

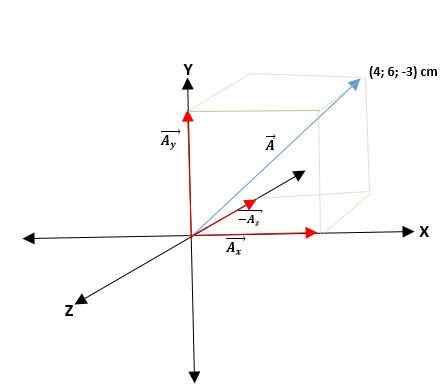
Vektor yang mempunyai koordinat segi empat tepat mereka boleh dinyatakan mengikut vektor asas mereka. Untuk itu, hanya setiap koordinat mesti didarabkan oleh vektor unit masing -masing, supaya untuk pesawat dan ruang mereka akan menjadi yang berikut:

Untuk pesawat: ā = a_xi +a_danJ.

Untuk ruang: ā = a_xi +a_danJ+a_zk.

Operasi dengan vektor

Terdapat banyak magnitud yang mempunyai modul, makna dan arah, seperti pecutan, kelajuan, perpindahan, daya, antara lain.

Ini digunakan dalam pelbagai bidang sains, dan untuk menerapkannya, perlu dalam beberapa kes untuk melaksanakan operasi seperti jumlah, penolakan, pendaraban dan pembahagian vektor dan skalar.

penambahan dan penolakan vektor

Jumlah dan penolakan vektor dianggap satu operasi algebra tunggal kerana penolakan boleh ditulis sebagai jumlah; Sebagai contoh, penolakan vektor ā dan ē boleh dinyatakan sebagai:

Ā - ē = ā + (-ē)

Terdapat kaedah yang berbeza untuk melaksanakan jumlah dan penolakan vektor: mereka boleh menjadi grafik atau analisis.

Kaedah grafik

Digunakan apabila vektor mempunyai modul, rasa dan arah. Untuk ini, garis ditarik yang membentuk angka yang kemudiannya membantu menentukan yang dihasilkan. Antara yang paling terkenal adalah yang berikut:

Kaedah Parallelogram

Untuk membuat jumlah atau penolakan dua vektor, titik umum dipilih pada paksi koordinat -yang akan mewakili titik asal vektor -, mengekalkan modul, arah dan arah mereka.

Kemudian garisan selari ditarik ke vektor untuk membentuk selaras. Vektor yang dihasilkan adalah pepenjuru yang meninggalkan dari titik asal kedua -dua vektor ke puncak paralelogram:

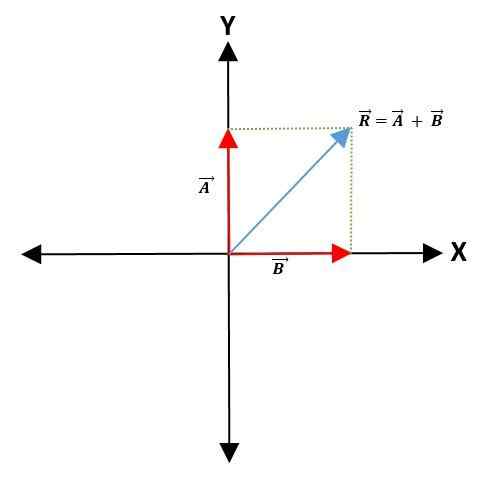
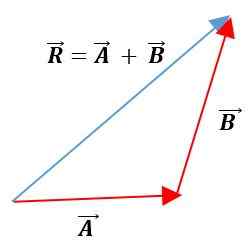
Kaedah Segitiga

Dalam kaedah ini vektor diletakkan di bawah yang lain, mengekalkan modul, deria dan alamat mereka. Vektor yang dihasilkan akan menjadi kesatuan asal vektor pertama dengan akhir vektor kedua:

Kaedah analisis

Dua atau lebih vektor boleh ditambah atau dikurangkan melalui kaedah geometri atau vektor:

Kaedah Geometrik

Apabila dua vektor membentuk segitiga atau paralelogram, m [odulo dan arah vektor yang dihasilkan dapat ditentukan menggunakan undang -undang payudara dan kosinus. Oleh itu, modul vektor yang dihasilkan, menggunakan undang -undang kosinus dan kaedah segitiga, diberikan oleh:

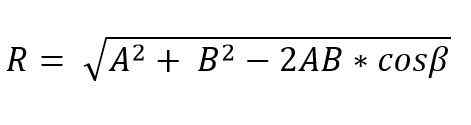
Dalam formula ini β adalah sudut bertentangan ke sisi r, dan ini sama dengan 180º - ɵ.

Sebaliknya, dengan kaedah paralelogram modul vektor yang dihasilkan ialah:

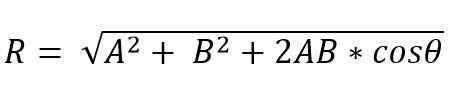
Alamat vektor yang dihasilkan diberikan oleh sudut (α), yang membentuk yang dihasilkan dengan salah satu vektor.

Dengan undang -undang payudara, jumlah atau penolakan vektor juga boleh dilakukan oleh kaedah segitiga atau paralelogram, mengetahui bahawa dalam setiap segitiga sisi adalah berkadar dengan payudara sudut kacak:

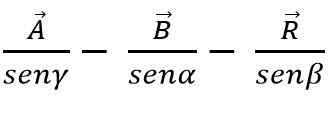
Kaedah vektor

Ini boleh dilakukan dalam dua cara: bergantung pada koordinat segi empat tepat atau vektor asasnya.

Vektor yang akan ditambah atau dikurangkan ke arah asal koordinat boleh dilakukan, dan kemudian semua unjuran dipecahkan ke dalam komponen segi empat tepat mereka dalam setiap paksi untuk satah (x, y) atau ruang (x, x, dan z); Akhirnya, komponennya ditambah secara algebra. Jadi, untuk pesawat itu:

Boleh melayani anda: Nombor Primo: Ciri, Contoh, Latihan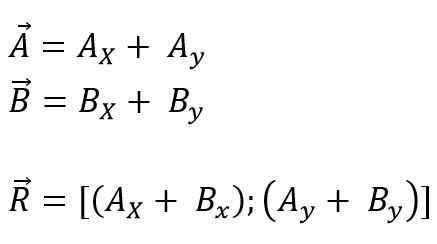

Modul vektor yang dihasilkan ialah:

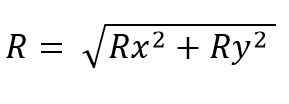
Sementara untuk ruang itu:

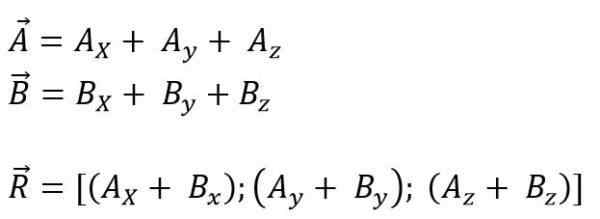
Modul vektor yang dihasilkan ialah:

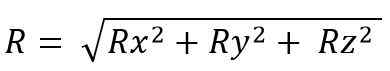
Apabila jumlah vektor dijalankan, beberapa sifat digunakan, iaitu:

• Harta bersekutu: Hasilnya tidak berubah dengan menambahkan dua vektor terlebih dahulu, dan kemudian menambah vektor ketiga.
• Harta komutatif: Susunan vektor tidak mengubah yang dihasilkan.
• Harta pengedaran vektor: Sekiranya skalar didarab dengan jumlah dua vektor, ia sama dengan pendaraban skalar untuk setiap vektor.
• Skalar harta pengedaran: Sekiranya vektor didarab dengan jumlah dua skalar, ia sama dengan pendaraban vektor untuk setiap skalar.

Pendaraban vektor

Pendaraban atau produk vektor boleh dijalankan sebagai jumlah atau penolakan, tetapi dengan berbuat demikian ia kehilangan makna fizikal dan hampir tidak pernah dalam aplikasi. Oleh itu, umumnya jenis produk yang paling banyak digunakan ialah produk skalar dan vektor.

Produk skalar

Ia juga dikenali sebagai titik dua vektor. Apabila modul dua -vektor didarabkan oleh kosinus sudut kecil yang terbentuk di antara mereka, skalar diperolehi. Untuk menyatakan produk skalar antara dua vektor, titik di antara mereka diletakkan, dan ini boleh ditakrifkan sebagai:

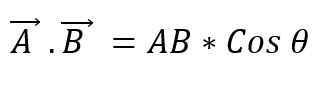
Nilai sudut yang wujud di antara kedua -dua vektor akan bergantung kepada sama ada ini selari atau tegak lurus; Oleh itu, anda mesti:

• Sekiranya vektor selari dan mempunyai rasa yang sama, coseno 0º = 1.
• Sekiranya vektor selari dan mempunyai deria bertentangan, Coseno 180º = -1.
• Sekiranya vektor berserenjang, Coseno 90º = 0.

Sudut itu juga boleh dikira mengetahui bahawa:

Produk skalar mempunyai sifat berikut:

• Harta Komutatif: Perintah vektor tidak mengubah skalar.
• Harta Pengedaran: Jika skalar didarabkan dengan jumlah dua vektor, ia sama dengan pendaraban skalar untuk setiap vektor.

Produk vektor

Pendaraban vektor, atau produk silang dua vektor A dan B, akan menghasilkan vektor baru C dan menyatakan menggunakan salib di antara vektor:

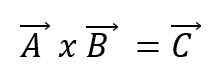
Vektor baru akan mempunyai ciri -ciri tersendiri. Jalan itu:

• The alamat: Vektor baru ini akan berserenjang dengan satah, yang ditentukan oleh vektor asal.
• Dia rasa: Ini ditentukan dengan peraturan tangan kanan, di mana vektor A beralih ke b yang menunjuk arah putaran dengan jari, dan dengan ibu jari arah arah vektor ditandakan.
• Dia modul: Ia ditentukan oleh pendaraban modul vektor AXB, oleh pangkuan sudut kecil yang wujud di antara vektor ini. Ia dinyatakan:

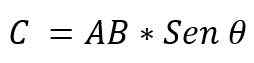
Nilai sudut yang wujud antara kedua -dua vektor akan bergantung kepada sama ada ini selari atau tegak lurus. Oleh itu, adalah mungkin untuk mengesahkan perkara berikut:

• Sekiranya vektor selari dan mempunyai makna yang sama, sine 0º = 0.
• Sekiranya vektor selari dan mempunyai deria yang bertentangan, sine 180º = 0.
• Sekiranya vektor berserenjang, sinus 90º = 1.

Apabila produk vektor dinyatakan mengikut vektor asasnya, ia harus:

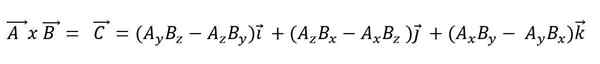
Produk skalar mempunyai sifat berikut:

• Ia bukan komutatif: susunan vektor mengubah skalar.
• Harta Pengedaran: Jika skalar didarabkan dengan jumlah dua vektor, ia sama dengan pendaraban skalar untuk setiap vektor.