Magnitud vektor

Apakah magnitud vektor?

A Magnitud vektor Ini adalah ungkapan yang diwakili oleh vektor yang mempunyai nilai berangka (modul), arah, arah dan titik aplikasi. Beberapa contoh magnitud vektor adalah anjakan, kelajuan, kekuatan dan medan elektrik.

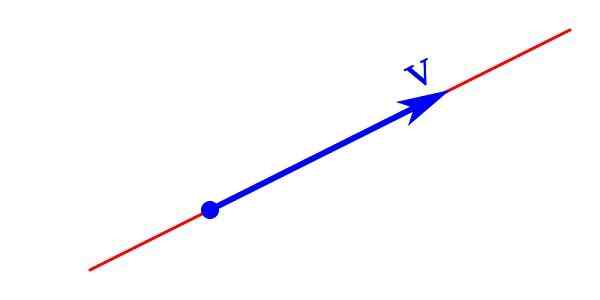
Perwakilan grafik magnitud vektor terdiri daripada anak panah yang tipnya menunjukkan arah dan arahnya, panjangnya adalah modul dan titik permulaan adalah asal atau titik aplikasi.

Perwakilan grafik vektor

Magnitud vektor diwakili secara analitik dengan surat yang membawa anak panah di bahagian atas menunjuk ke kanan ke arah mendatar. Ia juga boleh diwakili oleh surat yang ditulis dengan berani V yang modul ǀVǀ Ia ditulis dalam huruf miring V.

Salah satu aplikasi konsep magnitud vektor adalah dalam reka bentuk lebuh raya dan jalan raya, khususnya dalam reka bentuk kelengkungannya. Permohonan lain ialah pengiraan anjakan antara dua tempat atau perubahan kelajuan kenderaan.

Unsur magnitud vektor

Magnitud vektor adalah mana -mana entiti yang diwakili oleh segmen garis, dengan orientasi di ruang angkasa, yang mempunyai ciri -ciri vektor. Unsur -unsurnya adalah:

Modul: Ia adalah nilai berangka yang menunjukkan saiz atau intensiti magnitud vektor.

Alamat: Ia adalah orientasi segmen garis di ruang yang mengandunginya. Vektor boleh mempunyai arah mendatar, menegak atau cenderung; Utara, selatan, ini atau barat; Timur laut, tenggara, barat daya atau barat laut.

Rasa: Ia ditunjukkan dengan hujung anak panah di hujung vektor.

Ia boleh melayani anda: Fizik Sebelum Orang Yunani (Antigua Greece)

Titik permohonan: Ia adalah asal atau titik tindakan awal vektor.

Klasifikasi Vektor

Vektor diklasifikasikan sebagai collinear, selari, berserenjang, serentak, gandum, bebas, gelongsor, bertentangan, peralatan, tetap dan unit.

Colineal: Mereka tergolong atau bertindak pada garis lurus yang sama, mereka juga dipanggil bergantung secara linear Dan mereka boleh menegak, mendatar dan cenderung.

Parallels: Mereka mempunyai alamat atau kecenderungan yang sama.

Tegak lurus: Dua vektor berserenjang antara satu sama lain apabila sudut di antara mereka adalah 90 °.

Serentak: Mereka adalah vektor yang ketika meluncur ke atas garis tindakan mereka, mereka bertepatan pada titik yang sama di ruang angkasa.

Coplanarios: Mereka bertindak dalam kapal terbang, contohnya pesawat Xy.

Percuma: Mereka bergerak ke mana -mana di ruang yang menjaga modul, arah dan makna mereka.

Gelongsor: Mereka bergerak sepanjang garis tindakan yang ditentukan oleh arah mereka.

Berlawanan: Mereka mempunyai modul dan arah yang sama, dan arah yang bertentangan.

Peralatan: Mereka mempunyai modul, arah dan makna yang sama.

Tetap: Titik permohonan tidak dapat dilanggar.

Persatuan: Vektor yang modulnya adalah unit.

Komponen vektor

Magnitud vektor dalam ruang tiga dimensi diwakili dalam sistem tiga paksi serenjang antara satu sama lain (X dan z) dipanggil ortogonal cuba.

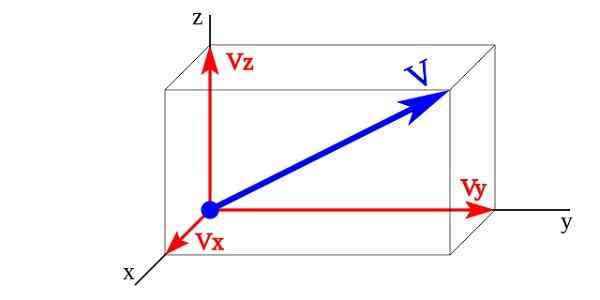Komponen vektor magnitud vektor

Dalam gambar vektor Vx, Vy, Vz adalah komponen vektor vektor V vektor unit yang x,dan,z. Magnitud vektor V Ia diwakili oleh jumlah komponen vektornya.

V = Vx + Vy + Vz

Hasil dari beberapa magnitud vektor adalah jumlah vektor semua vektor dan menggantikan vektor ini dalam sistem.

Medan vektor

Medan vektor adalah kawasan ruang di mana di setiap titiknya magnitud vektor sesuai. Sekiranya magnitud yang ditunjukkan adalah daya yang bertindak pada badan atau sistem fizikal maka medan vektor adalah bidang daya.

Boleh melayani anda: Steiner Theorem: Penjelasan, Aplikasi, Latihan

Medan vektor diwakili secara grafik oleh garis medan yang merupakan garis tangen magnitud vektor di semua titik di rantau ini. Beberapa contoh medan vektor adalah medan elektrik yang dicipta oleh cas elektrik tepat pada masanya di ruang dan kelajuan medan bendalir.

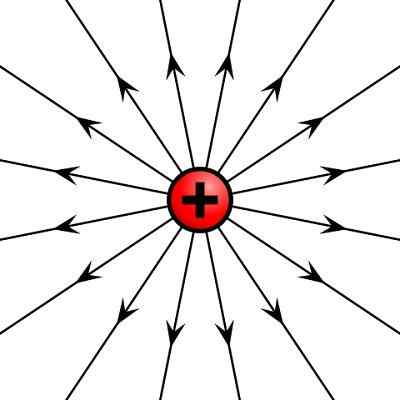Medan elektrik yang dibuat oleh caj elektrik yang positif

Operasi dengan vektor

Penambahan vektor: Ia adalah hasil daripada dua atau lebih vektor. Sekiranya anda mempunyai dua vektor Sama ada dan P Jumlahnya Sama ada + P = q. Vektor Q Ia adalah vektor yang dihasilkan yang diperoleh secara grafik menggerakkan asal vektor Ke hingga akhir vektor B.

Penolakan vektor: Penolakan dua vektor atau dan P adalah Sama ada - P = Q. Vektor Q  Anda akan menambah vektor Sama ada Sebaliknya -P. Kaedah grafik adalah sama dengan jumlah dengan perbezaan bahawa vektor bertentangan dipindahkan ke yang melampau.

Produk skalar: Produk magnitud skalar ke dengan magnitud vektor P Ia adalah vektor MP yang mempunyai arah yang sama dari vektor P. Sekiranya magnitud skalar adalah sifar produk skalar adalah vektor null.

Contoh magnitud vektor

Kedudukan

Kedudukan objek atau zarah berkenaan dengan sistem rujukan adalah vektor yang diberikan oleh koordinat segi empat tepatnya X dan z, dan diwakili oleh komponen vektornya Xî, Yĵ, Zk. Vektor  Yo, ĵ, k Mereka adalah vektor unit.

Zarah pada satu titik (X dan z) mempunyai vektor kedudukan r = Xî + Yĵ + Zk. Nilai berangka kedudukan vektor adalah r= √ (x² + dan² + z²). Perubahan dalam kedudukan zarah dari satu kedudukan ke yang lain berkenaan dengan sistem rujukan adalah vektor Anjakan ΔR Dan ia dikira dengan ungkapan vektor berikut:

Boleh melayani anda: sinar anodik

ΔR = r₂ - r₁

Pecutan

Purata pecutan (ke_m) Ia ditakrifkan sebagai variasi kelajuan v Dalam selang waktu Δt Dan ungkapan untuk mengira ia adalah ke_m= ΔV/ΔT, menjadi ΔV Kelajuan perubahan vektor.

Pecutan segera (ke) adalah had pecutan purata ke_m bila Δt menjadi sangat kecil sehingga ia cenderung menjadi sifar. Percepatan segera dinyatakan mengikut komponen vektornya

ke =ke_xYo +ke_dan ĵ+ ke_zk

Medan graviti

Daya tarikan graviti yang dikenakan oleh jisim M, Terletak di asal, pada jisim yang lain m Pada satu titik di ruang angkasa x, dan, z Ia adalah medan vektor yang disebut medan daya graviti. Daya ini diberikan oleh ungkapan:

F= (-mmg/r)ȓ

r = Xî + Yĵ + Zk

F = Ia adalah daya graviti magnitud fizikal

G = adalah pemalar graviti sejagat

ȓ = Adakah vektor kedudukan massa m

Rujukan

1. Tallack, J C. Pengenalan kepada Analisis Vektor. Cambridge: Cambridge University Press, 2009.
2. Spiegel, M R, Lipschutz, S dan Spellman, D. Analisis vektor. s.L. : MC Graw Hill, 2009.
3. Jenama, l. Analisis vektor. New York: Dover Publications, 2006.
4. Griffiths, D J. Pengenalan kepada Elektrodinamik. New Jersey: Prentice Hall, 1999. p. 1-10.
5. Hague, b. Pengenalan kepada Analisis Vektor. Glasgow: Methuen & Co. Ltd, 2012.