Pengiraan dan senaman matriks songsang diselesaikan
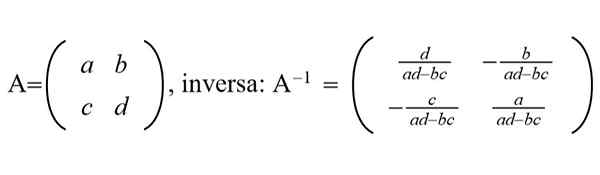
- 3501
- 609
- Anthony Breitenberg
The Matriks songsang daripada matriks yang diberikan, ia adalah matriks yang didarabkan oleh hasil asal dalam matriks identiti. Matriks terbalik berguna untuk menyelesaikan sistem persamaan linear, oleh itu pentingnya mengetahui cara mengiranya.
Matriks sangat berguna dalam fizik, kejuruteraan dan matematik, kerana mereka adalah alat padat untuk menyelesaikan masalah yang rumit. Utiliti matriks dipertingkatkan apabila mereka terbalik dan juga terbalik mereka.
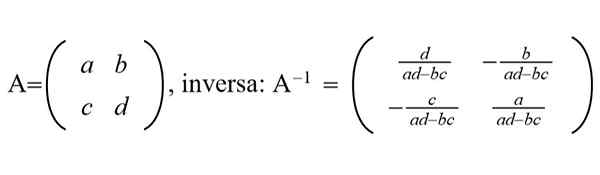 Rajah 1. Matriks 2 × 2 generik dan matriks songsang ditunjukkan. (Disediakan oleh Ricardo Pérez)
Rajah 1. Matriks 2 × 2 generik dan matriks songsang ditunjukkan. (Disediakan oleh Ricardo Pérez) Dalam bidang pemprosesan grafik, data besar, perlombongan data, pembelajaran mesin dan lain -lain digunakan algoritma yang cekap dan cepat untuk menilai matriks matriks NXN dengan N sangat besar, mengikut urutan beribu -ribu atau berjuta -juta.
Untuk menggambarkan penggunaan matriks terbalik dalam pengurusan sistem persamaan linear kita akan bermula dengan kes paling mudah semua: 1 × 1 matriks.
Kes paling mudah: Persamaan linear satu pembolehubah dipertimbangkan: 2 x = 10.
Ideanya adalah untuk mencari nilai x, tetapi ia akan menjadi "matriks".
Matriks m = (2) yang mengalikan vektor (x) adalah matriks 1 × 1 yang menghasilkan vektor (10):
M (x) = (10)
Kebalikan dari matriks M dilambangkan oleh m-1.
Cara umum menulis "sistem linear" ini adalah:
M x = b, di mana x adalah vektor (x) dan b ialah vektor (10).
Secara definisi, matriks terbalik adalah salah satu yang didarabkan oleh matriks asal menghasilkan matriks identiti i:
M-1 M = i
Dalam kes yang dipertimbangkan, matriks m-1 Ia adalah matriks (½), iaitu m-1 = (½) Sejak m-1 M = (½) (2) = (1) = i
Boleh melayani anda: 90 pembahagi: Apa dan penjelasanUntuk mencari vektor yang tidak diketahui x = (x), dalam persamaan yang dibangkitkan, kedua -dua ahli didarab dengan matriks terbalik:
M-1 M (x) = m-1 (10)
(½) (2) (x) = (½) (10)
(½ 2) (x) = (½ 10)
(1) (x) = (5)
(x) = (5)
Kesamaan dua vektor telah dicapai, yang sama hanya apabila unsur -unsur yang sama adalah sama, iaitu x = 5.
Pengiraan terbalik matriks
Apa yang mendorong pengiraan matriks terbalik adalah untuk mencari kaedah sejagat untuk penyelesaian sistem linear seperti sistem 2 × 2 berikut:
x - 2 y = 3
-x + y = -2
Berikutan langkah -langkah kes 1 × 1, dikaji di bahagian sebelumnya, kami menulis sistem persamaan dalam cara matriks:
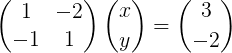 Rajah 2. Sistem linear dalam bentuk matriks.
Rajah 2. Sistem linear dalam bentuk matriks. Perhatikan bahawa sistem ini ditulis dalam notasi vektor padat seperti berikut:
M x = b
di mana
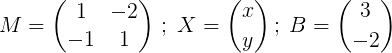
Langkah seterusnya adalah mencari m.
Kaedah 1: Melalui Penghapusan Gaussian
Kaedah Penghapusan Gauss akan digunakan. Yang terdiri daripada melakukan operasi asas pada pangkat matriks, operasi ini adalah:
- Melipatgandakan baris dengan nombor bukan null.
- Tambah atau tolak baris lain, atau pelbagai baris lain.
- Baris pertukaran.
Objektifnya, melalui operasi ini, untuk menukar matriks asal ke dalam matriks identiti.
Seperti yang dilakukan, dalam matriks m betul -betul operasi yang sama dengan matriks identiti digunakan. Apabila selepas beberapa operasi dalam baris R ia diubah menjadi matriks kesatuan, maka yang pada asalnya adalah kesatuan akan diubah menjadi matriks terbalik m, iaitu, m-1.
Boleh melayani anda: Corollary (geometri)1- Kami memulakan proses dengan menulis matriks m dan di sebelahnya matriks unit:
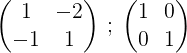
2- Kami menambah dua baris dan hasilnya dimasukkan ke dalam barisan kedua, dengan cara ini kita mendapat sifar dalam elemen pertama baris kedua:
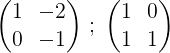
3- Kami melipatgandakan baris kedua dengan -1 untuk mendapatkan 0 dan 1 pada baris kedua:
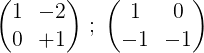
4- Baris pertama didarab dengan ½:

5- Yang kedua dan yang pertama menambah dan hasilnya diletakkan di barisan hadapan:
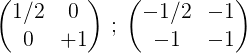
6- Untuk mengakhiri proses, baris pertama oleh 2 didarabkan untuk mendapatkan pada pertama matriks identiti dan pada kedua matriks terbalik matriks asal m:
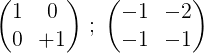
Iaitu:
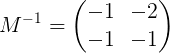
Penyelesaian sistem
Sebaik sahaja matriks terbalik diperoleh, sistem persamaan diselesaikan dengan menggunakan matriks terbalik dalam kedua -dua ahli persamaan vektor padat:
M-1M x = m-1B
X = m-1B
Yang secara eksplisit tetap seperti ini:
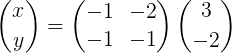
Kemudian pendaraban matriks dibuat untuk mendapatkan vektor x:
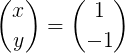
Kaedah 2: Dengan matriks yang dilampirkan
Dalam kaedah kedua ini matriks terbalik dikira berdasarkan matriks yang dilampirkan matriks asal Ke.
Katakan matriks yang diberikan oleh:

kemanaSaya, j Ia adalah elemen baris Yo dan lajur J daripada matriks Ke.
Lampiran matriks Ke Ia akan dipanggil Adj (a) Dan unsur -unsurnya adalah:
ADSaya, j = (-1)(i+j) U, J |
di mana Ai, j Ia adalah matriks kecil pelengkap yang diperoleh dengan menghapuskan baris I dan lajur j dari matriks asal Ke. Bar | | menunjukkan bahawa penentu dikira, iaitu U, J | Ia adalah penentu matriks kecil pelengkap.
Boleh melayani anda: sisi homologFormula matriks songsang
Formula untuk mencari matriks terbalik berdasarkan matriks yang dilampirkan matriks asal adalah seperti berikut:
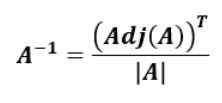
Iaitu matriks terbalik Ke, Ke-1, adalah transpose lampiran Ke dibahagikan dengan penentu Ke.
Yang ditukar KeTdaripada matriks Ke Ia adalah yang diperoleh dengan bertukar pangkat untuk lajur, ia.
Latihan diselesaikan
Jadilah matriks ke seterusnya:
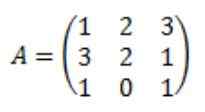
Setiap elemen matriks yang dilampirkan A: adj (a) dikira
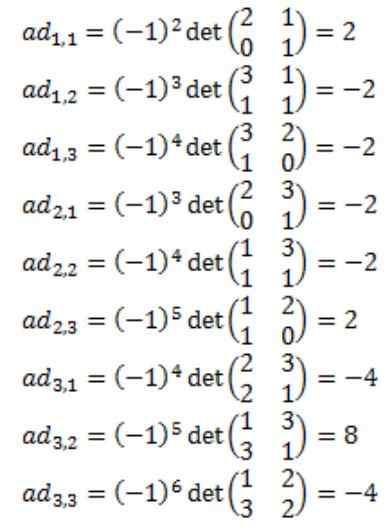
Mengakibatkan matriks yang dilampirkan A, adj (a) adalah seperti berikut:
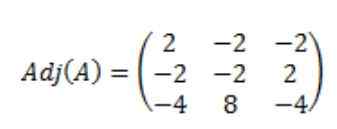
Kemudian penentu matriks A, det (a) dikira:
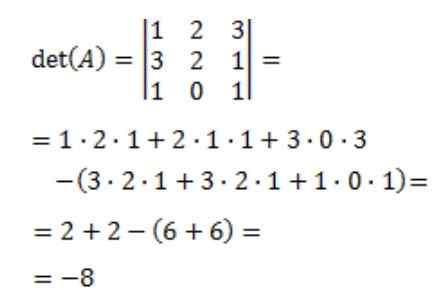
Akhirnya matriks terbalik A diperoleh:
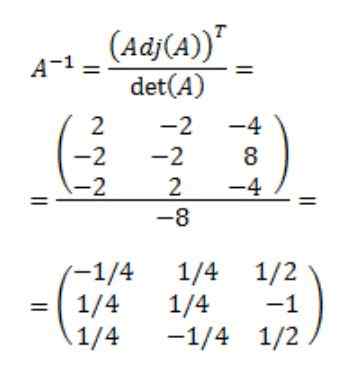
Rujukan
- Anthony Nicolaides (1994) Penentu & Matriks. Lulus penerbitan.
- Awol Assen (2013) Kajian mengenai pengiraan penentu 3 × 3
- Casteleiro Villalba m. (2004) Pengenalan kepada aljabar linear. Editorial ESIC.
- Dave Kirkby (2004) Matematik Menyambung. Heinemann.
- Jenny Olive (1998) Matematik: Panduan Survival Pelajar. Cambridge University Press.
- Richard J. Brown (2012) Matematik 30 saat: 50 Teori Paling Minda yang Paling Minda dalam Matematik. Ivy Press Limited.
- Matriks. Penerbitan Akademik Lap Lambert.
- « Ciri -ciri, Jenis, Kegunaan Sederhana Budaya Separuh Budaya
- Penerangan Kalendar Maya, Bagaimana Kerja, Sistem »

