Ciri -ciri Pergerakan Rectilinear Seragam, Formula, Latihan

Dia Pergerakan garis seragam atau pada kelajuan tetap adalah satu di mana zarah bergerak di sepanjang garis lurus dan dengan kelajuan yang berterusan. Dengan cara ini, mudah alih bergerak jarak yang sama dengan masa yang sama. Sebagai contoh, jika dalam 1 saat ia bergerak 2 meter, selepas 2 saat akan ada 4 meter dan sebagainya.

Untuk membuat keterangan yang tepat mengenai pergerakan itu, sama ada rektilinar seragam atau yang lain, adalah perlu untuk mewujudkan titik rujukan, juga dipanggil asal, mengenai kedudukan mudah alih yang mana kedudukannya.

Rajah 1. Sebuah kereta yang bergerak di sepanjang jalan rectilinear pada kelajuan berterusan mempunyai pergerakan rectilinear seragam. Sumber: Pixabay.

Sekiranya pergerakan itu berlalu sepenuhnya di sepanjang garis lurus, ia juga berminat untuk mengetahui dalam erti kata perjalanan mudah alih.

Pada garis mendatar, ada kemungkinan mudah alih pergi ke kanan atau ke kiri. Perbezaan antara kedua-dua situasi dibuat oleh tanda-tanda, yang berikut adalah yang berikut: di sebelah kanan saya ikuti (+) dan tanda kiri (-).

Apabila kelajuan tetap, mudah alih tidak mengubah arahnya atau maknanya, dan juga magnitud kelajuannya tetap tidak berubah.

[TOC]

Ciri -ciri

Ciri -ciri utama pergerakan rectilinear seragam (MRU) adalah berikut:

-Pergerakan selalu berlalu sepanjang garis lurus.

-Mudah alih dengan MRU bergerak jarak atau ruang yang sama dengan masa yang sama.

-Kelajuan kekal tidak dapat diubah baik dalam magnitud dan arah.

-MRU tidak mempunyai pecutan (tidak ada perubahan kelajuan).

-Sejak kelajuan v tetap berterusan dari masa ke masa t, Graf magnitudnya sebagai fungsi masa adalah garis lurus. Dalam contoh Rajah 2, garisannya hijau dan nilai kelajuan dibaca pada paksi menegak, kira -kira +0.68 m/s.

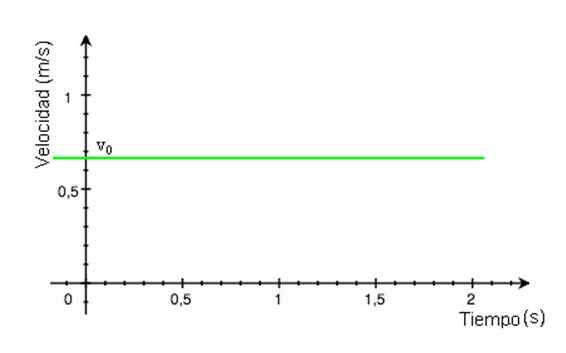Rajah 2. Graf kelajuan bergantung pada MRU. Sumber: Wikimedia Commons.

-Grafik kedudukan X berkenaan dengan masa adalah garis lurus, yang cerunnya bersamaan dengan kelajuan mudah alih. Sekiranya garis graf x vs t adalah mendatar, mudah alih adalah berehat, jika cerun positif (graf angka 3), kelajuan juga.

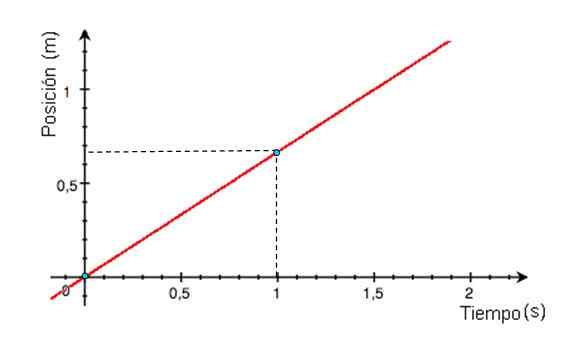Rajah 3. Graf kedudukan sebagai fungsi masa untuk telefon bimbit dengan MRU yang berlepas dari asal. Sumber: Wikimedia Commons.

Jarak perjalanan dari graf v vs. t

Ketahui jarak yang dilalui oleh mudah alih apabila graf tersedia V Vs. t sangat sederhana. Jarak perjalanan bersamaan dengan kawasan di bawah garis dan dimasukkan dalam selang waktu yang diingini.

Ia dapat melayani anda: pecutan purata: bagaimana ia dikira dan diselesaikan

Katakan anda ingin mengetahui jarak yang dilalui oleh mudah alih Rajah 2 dalam selang antara 0.5 dan 1.5 saat.

Kawasan ini adalah segi empat tepat yang berlorek dalam Rajah 4. Ia dikira dengan mencari hasil mengalikan asas segi empat tepat dengan ketinggiannya, yang nilainya dibaca dari grafik.

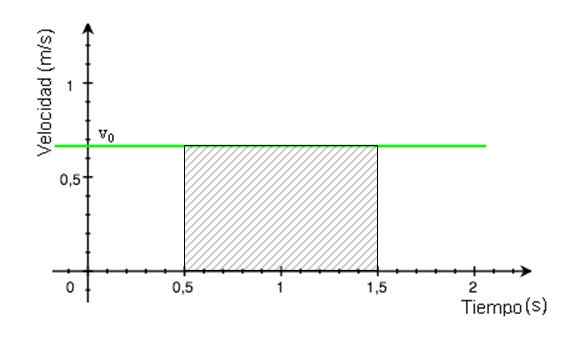Rajah 4. Kawasan berjalur bersamaan dengan jarak perjalanan. Sumber: Wikimedia Commons diubahsuai.

Jarak perjalanan = (1.lima puluh.5) x 0.68 m = 0.68 m

Jarak selalu jumlah positif, tidak kira sama ada anda pergi ke kanan atau ke kiri.

Formula dan persamaan

Di MRU, kelajuan purata dan kelajuan serta -merta sentiasa sama dan kerana nilainya adalah cerun graf x vs t yang sepadan dengan garis, persamaan yang sepadan bergantung pada masa adalah berikut:

-Kedudukan bergantung pada masa: x (t) = x_{Sama ada} + Vt

x_{Sama ada} Ia mewakili kedudukan awal mudah alih, pada banyak kesempatan ia bertepatan dengan asal sistem rujukan, tetapi tidak selalu seperti ini. Persamaan ini juga dikenali sebagai Persamaan jadual.

-Kelajuan bergantung pada masa: v (t) = malar

Bila V = 0 bermaksud bahawa mudah alih berehat. Rehat adalah kes pergerakan tertentu.

-Pecutan sebagai fungsi masa: A (t) = 0

Dalam pergerakan rectilinear seragam tidak ada perubahan kelajuan, oleh itu pecutan adalah sifar.

Latihan yang diselesaikan

Pada masa menyelesaikan latihan, perlu dipastikan bahawa keadaan sepadan dengan model yang akan digunakan. Khususnya sebelum menggunakan persamaan MRU, adalah perlu untuk memastikan bahawa ia berkenaan.

Latihan berikut diselesaikan adalah dua masalah mudah alih.

Latihan diselesaikan 1

Dua atlet saling menghampiri dengan cepat 4.50 m/s dan 3.5 m/s masing -masing, pada mulanya dipisahkan jarak 100 meter, seperti yang ditunjukkan dalam angka tersebut.

Sekiranya setiap orang mengekalkan kelajuannya yang berterusan, cari: a) berapa lama masa yang diperlukan untuk bertemu? b) Apa yang akan menjadi kedudukan masing -masing pada masa itu?

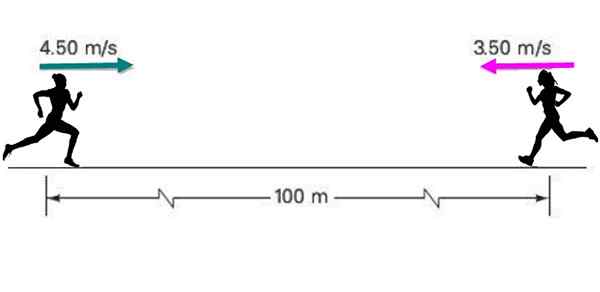Rajah 5. Dua pelari bergerak ke satu sama lain. Sumber: Diri Diri.

Penyelesaian

Yang pertama adalah untuk menunjukkan asal -usul sistem koordinat yang akan menjadi rujukan. Pilihan bergantung pada keutamaan bahawa orang yang menyelesaikan masalah itu ada.

Boleh melayani anda: Apakah dilebarkan volumetrik? (Dengan contoh)

Ia biasanya dipilih x = 0 tepat di titik permulaan telefon bimbit, ia boleh berada di pelari kiri atau kanan, bahkan boleh dipilih di tengah -tengah kedua -duanya.

a) Kami akan memilih x = 0 pada pelari kiri atau pelari 1, oleh itu kedudukan awal ini adalah x₀₁ = 0 dan untuk pelari 2 akan menjadi x₀₂ = 100 m. Broker 1 bergerak dari kiri ke kanan dengan kelajuan v₁ = 4.50 m/ sementara pelari 2 melakukannya dari kanan ke kiri dengan kelajuan -3.50 m/s.

Persamaan pergerakan untuk broker pertama

x₁ = x₀₁ + v₁t₁ = 4.50t₁

Persamaan pergerakan untuk broker kedua

x₂ = x₀₂ + v₂t₂ = 100 -3.50t₂

Seperti masa yang sama untuk kedua -duanya t₁ = t₂ = t , Apabila kedudukan kedua -duanya akan sama, oleh itu x₁ = x₂. Sama:

4.50t = 100 -3.50t

Ia adalah persamaan ijazah pertama untuk masa, yang penyelesaiannya adalah t = 12.5 s.

b) Kedua -dua pelari berada dalam kedudukan yang sama, oleh itu ia menggantikan masa yang diperoleh di bahagian sebelumnya dalam mana -mana persamaan kedudukan. Contohnya kita boleh menggunakan pelari 1:

x₁ = 4.50t₁ = 56.25 m

Hasil yang sama diperoleh dengan menggantikan t = 12.5 s dalam Persamaan Posisi Pelari 2.

-Latihan diselesaikan 2

Kelinci mencabar penyu untuk menjalankan jarak 2.4 km dan bersikap adil ia menawarkan kelebihan setengah jam. Dalam permainan, Turtle maju dengan alasan 0.25 m/s, yang maksimum yang boleh dijalankan. Selepas 30 minit kelinci berjalan pada 2 m/s dan sampai ke penyu dengan cepat.

Setelah meneruskan selama 15 minit lagi, fikir dia mempunyai masa untuk tidur siang dan masih memenangi perlumbaan, tetapi tertidur selama 111 minit. Ketika dia bangun, dia berjalan dengan segala kekuatannya, tetapi penyu sudah melintasi gol. Cari:

a) Apakah kelebihan penyu menang?

b) Momen masa di mana kelinci memajukan penyu

c) masa di mana penyu maju ke kelinci.

Penyelesaian untuk)

Perlumbaan bermula di t = 0. Kedudukan penyu: x_T = 0.25t

Pergerakan kelinci mempunyai bahagian berikut:

Boleh melayani anda: Sistem Suria: Planet, Ciri, Asal, Evolusi

-Rehat untuk kelebihan yang diberikan kepada penyu: 0 < t < 30 minutos:

-Perlumbaan untuk mencapai penyu dan terus berlari sedikit selepas lulus; Secara keseluruhan mereka adalah 15 minit pergerakan.

-Tidur selama 111 minit (rehat)

-Bangun terlambat (pecut akhir)

2.4 km = 2400 m

Tempoh perlumbaan adalah: T = 2400 m/ 0.25 m/s = 9600 s = 160 min. Pada masa ini kita tolak 111 minit dari tidur tidur dan 30 kelebihan, iaitu 19 minit (1140 saat). Ini bermaksud bahawa dia berlari selama 15 minit sebelum tidur dan 4 minit selepas bangun untuk pecut.

Pada masa ini kelinci menutup jarak berikut:

d_L = 2 m/s . (lima belas . 60 s) + 2 m/s (4. 60 s) = 1800 m + 480 m = 2280 m.

Oleh kerana jarak keseluruhannya adalah 2400 meter, menolak kedua -dua nilai, ternyata kelinci tidak mempunyai 120 meter untuk mencapai matlamat.

Penyelesaian b)

Kedudukan kelinci sebelum tertidur adalah x_L = 2 (t - 1800), Memandangkan kelewatan 30 -minut = 1800 saat. Sama dengan x_T dan x_L Kita dapati masa mereka:

2 (t - 1800) = 0.25t

2t -0.25 t = 3600

T = 2057.14 s = 34.29 min

Penyelesaian c)

Pada masa Hare maju oleh penyu, yang sedang tidur pada 1800 meter dari permainan:

1800 = 0.25t

T = 7200 s = 120 min

Aplikasi

MRU adalah pergerakan paling mudah yang dapat dibayangkan dan itulah sebabnya ia adalah yang pertama dikaji dalam sinematik, tetapi banyak pergerakan kompleks dapat digambarkan sebagai gabungan ini dan pergerakan mudah lain.

Sekiranya seseorang meninggalkan rumahnya dan memimpin sehingga dia sampai ke lebuh raya rectilinear yang panjang di mana dia bergerak dengan kelajuan yang sama untuk masa yang lama, pergerakannya sebagai MRU dapat diterangkan, tanpa masuk ke butiran lanjut.

Sudah tentu orang itu perlu mengambil beberapa pusingan sebelum memasuki dan meninggalkan lebuh raya, tetapi melalui penggunaan model pergerakan ini, tempoh perjalanan dapat dianggarkan mengetahui jarak dekat antara titik permulaan dan titik ketibaan.

Secara semula jadi, cahaya mempunyai gerakan rectilinear seragam yang kelajuannya 300.000 km/s. Juga pergerakan bunyi di udara boleh diandaikan rectilinear seragam dengan kelajuan 340 m/s dalam banyak aplikasi.

Semasa menganalisis masalah lain, contohnya pergerakan pembawa beban di dalam wayar konduktif, pendekatan MRU juga boleh digunakan untuk memberi gambaran tentang apa yang berlaku di dalam pemandu.

Rujukan

1. Bauer, w. 2011. Fizik untuk Kejuruteraan dan Sains. Jilid 1. MC Graw Hill.40-45.
2. Figueroa, d. Siri Fizikal untuk Sains dan Kejuruteraan. Jilid 3. Edisi. Kinematik. 69-85.
3. Giancoli, d.  Fizik: Prinsip dengan aplikasi. 6^th. Ed Prentice Hall. 19-36.
4. Hewitt, Paul. 2012. Sains Fizikal Konsep. 5^th. Ed. Pearson. 14-18.
5. Kirkpatrick, l. 2007. Fizik: Lihatlah dunia. 6^TA Edisi Singkat. Pembelajaran Cengage. 15-19.
6. Wilson, J. 2011. Fizik 10. Pendidikan Pearson. 116-119.