Metodologi pensampelan rawak, kelebihan, kekurangan, contoh

Dia pensampelan rawak Ini adalah cara untuk memilih sampel wakil statistik dari populasi tertentu. Sebahagian daripada prinsip bahawa setiap elemen sampel mesti mempunyai kebarangkalian yang sama dipilih.

Raffle adalah contoh pensampelan rawak, di mana setiap ahli penduduk peserta diberikan nombor. Untuk memilih nombor yang sepadan dengan Anugerah Raffle (sampel) beberapa teknik rawak digunakan, contohnya ekstrak dari peti mel nombor yang dijaringkan pada kad yang sama.

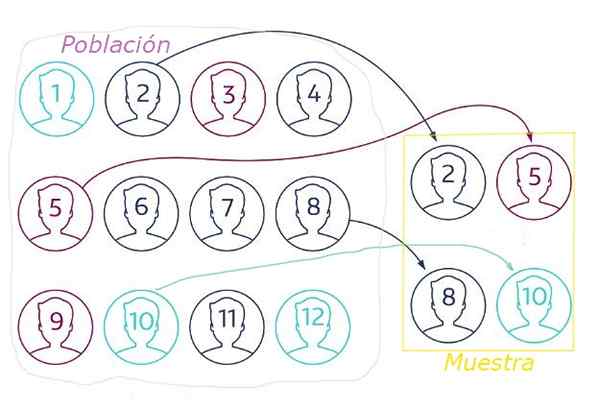Rajah 1. Dalam persampelan secara rawak, sampel diekstrak dari populasi rawak melalui beberapa teknik yang memastikan bahawa semua elemen mempunyai kebarangkalian yang sama dipilih. Sumber: Netquest.com.

Dalam persampelan secara rawak, ia penting.

[TOC]

Saiz sampel

Terdapat formula untuk menentukan saiz sampel yang betul. Faktor yang paling penting untuk dipertimbangkan ialah sama ada saiz penduduk diketahui atau tidak. Mari lihat formula untuk menentukan saiz sampel:

Kes 1: Saiz penduduk tidak diketahui

Apabila saiz penduduk tidak diketahui, adalah mungkin untuk memilih sampel N yang mencukupi, untuk menentukan sama ada hipotesis tertentu adalah benar atau palsu.

Untuk ini, formula berikut digunakan:

n = (z² P q)/(e²)

Di mana:

-P itu adalah kebarangkalian bahawa hipotesis itu benar.

-Q adalah kebarangkalian bahawa tidak, oleh itu q = 1 - p.

-E adalah margin relatif ralat, contohnya ralat 5% mempunyai margin e = 0.05. 

-Z mempunyai kaitan dengan tahap keyakinan yang diperlukan oleh kajian.

Boleh melayani anda: Pengagihan Normal: Formula, Ciri, Contoh, Latihan

Dalam pengedaran normal yang ditandatangani (atau dinormalisasi), tahap keyakinan 90% mempunyai z = 1,645, kerana kebarangkalian hasilnya adalah antara -1,645σ dan +1,645σ adalah 90%, di mana σ adalah sisihan standard.

Tahap amanah dan nilai z yang sepadan 

1.- Tahap keyakinan 50% sepadan dengan z = 0.675.

2.- 68.Tahap keyakinan 3% sepadan dengan z = 1.

3.- Tahap keyakinan 90% bersamaan dengan z = 1,645.

4.- Tahap keyakinan 95% sepadan dengan z = 1.96

5.- Tahap keyakinan 95.5% sepadan dengan z = 2.

6.- Tahap keyakinan 99.7% bersamaan dengan z = 3.

Contoh di mana formula ini boleh digunakan dalam kajian untuk menentukan berat purata kerikil pantai.

Jelas tidak mungkin untuk belajar dan menimbang semua kerikil pantai, jadi mudah.

Rajah 2. Untuk mengkaji ciri -ciri kerikil pantai, perlu memilih sampel rawak dengan bilangan wakilnya. (Sumber: Pixabay)

Kes 2: Saiz penduduk dikenali

Apabila bilangan n unsur -unsur yang membentuk populasi tertentu (atau alam semesta) diketahui, jika anda ingin memilih dengan sampel rawak mudah sampel sampel yang signifikan secara statistik, ini adalah formula: 

n = (z²p q n)/(n e² + Z²P Q)

Di mana:

-Z adalah pekali yang berkaitan dengan tahap kepercayaan.

-P adalah kebarangkalian kejayaan hipotesis.

-Q adalah kebarangkalian kegagalan dalam hipotesis, p + q = 1.

-N adalah saiz jumlah penduduk.

-E adalah kesilapan relatif hasil kajian.

Contoh

Metodologi untuk mengekstrak sampel banyak bergantung pada jenis kajian yang perlu dilakukan. Oleh itu, persampelan rawak mempunyai banyak aplikasi:

Boleh melayani anda: tanda -tanda kumpulan

Tinjauan dan soal selidik

Contohnya dalam tinjauan telefon, orang dipilih untuk dirujuk oleh penjana nombor rawak, yang terpakai di rantau ini di bawah kajian.

Sekiranya anda ingin memohon soal selidik kepada pekerja syarikat besar, maka pemilihan responden dapat digunakan melalui nombor pekerja mereka, atau nombor kad identiti.

Nombor ini juga mesti dipilih secara rawak, menggunakan penjana nombor rawak sebagai contoh.

Rajah 3. Soal selidik boleh digunakan secara rawak memilih peserta. Sumber: Pixabay.

QA

Sekiranya kajian itu ada di bahagian -bahagian yang dihasilkan oleh mesin, bahagian mesti dipilih secara rawak, tetapi banyak yang dibuat pada waktu yang berlainan pada hari itu, atau pada hari atau minggu yang berlainan.

Kelebihan

Pensampelan Rawak Ringkas:

- Ia membolehkan untuk mengurangkan kos kajian statistik, kerana tidak perlu mengkaji jumlah penduduk untuk mendapatkan hasil yang boleh dipercayai secara statistik, dengan tahap kepercayaan yang dikehendaki dan tahap ralat yang diperlukan dalam kajian ini.

- Elakkan Bias: Sebagai pilihan unsur -unsur yang perlu dikaji secara rawak, kajian itu dengan setia mencerminkan ciri -ciri penduduk, walaupun hanya sebahagian daripada yang sama dipelajari.

Kekurangan

- Kaedah ini tidak mencukupi dalam kes -kes yang anda ingin tahu keutamaan dalam kumpulan yang berlainan atau strata penduduk.

Dalam kes ini, lebih baik untuk menentukan kumpulan atau segmen di mana kajian itu dilakukan. Sebaik sahaja strata atau kumpulan telah ditakrifkan, maka jika mudah bagi setiap mereka untuk menggunakan persampelan rawak.

- Tidak mungkin maklumat mengenai sektor minoriti diperoleh, yang kadang -kadang perlu mengetahui ciri -ciri mereka.

Boleh melayani anda: Simpson Rule: Formula, Demonstrasi, Contoh, Latihan

Sebagai contoh, jika ia merupakan kempen pada produk yang mahal, perlu mengetahui keutamaan sektor minoriti terkaya.

Latihan diselesaikan

Kami ingin mengkaji keutamaan penduduk dengan cara cola cola, tetapi tidak ada kajian terdahulu dalam populasi itu, yang saiznya tidak diketahui.

Sebaliknya, sampel harus mewakili tahap keyakinan minimum sebanyak 90% dan kesimpulan mesti mempunyai kesilapan peratusan sebanyak 2%.

-Cara menentukan saiz sampel?

-Apa yang akan menjadi saiz sampel jika margin ralat dibuat sehingga 5%?

Penyelesaian

Oleh kerana saiz populasi tidak diketahui, untuk menentukan saiz sampel, formula yang diberikan di atas digunakan:

n = (z²P q)/(e²)

Kami mengandaikan bahawa terdapat kebarangkalian yang sama keutamaan (p) dengan penyegaran kami bahawa bukan -preeference (q), kemudian p = q = 0.5.

Sebaliknya, kerana hasil kajian mesti mempunyai ralat peratusan kurang daripada 2%, maka ralat relatif akan menjadi 0.02.

Akhirnya, nilai z = 1,645 menghasilkan tahap keyakinan 90%.

Singkatnya, anda mempunyai nilai berikut:

Z = 1,645

P = 0.5

Q = 0.5

E = 0.02

Dengan data ini saiz sampel minimum dikira:

N = (1,645² 0.5 0.5)/(0.02²) = 1691.3

Ini bermakna bahawa kajian dengan margin kesilapan yang diperlukan dan dengan tahap keyakinan yang dipilih, mesti mempunyai sampel responden sekurang -kurangnya 1692 individu, dipilih oleh persampelan rawak mudah.

Jika anda pergi dari margin ralat dari 2% hingga 5%, maka saiz sampel baru ialah:

N = (1,645² 0.5 0.5)/(0.05²) = 271

Yang merupakan bilangan individu yang jauh lebih rendah. Kesimpulannya, saiz sampel sangat sensitif terhadap margin yang dikehendaki dalam kajian.

Rujukan

1. Berenson, m. 1985.Statistik untuk Pentadbiran dan Ekonomi, Konsep dan Aplikasi. Editorial Inter -American.
2. Statistik. Pensampelan rawak. Diambil dari: EncyclopeDiaeconomica.com.
3. Statistik. Pensampelan. Pulih dari: statistik.Mat.USON.mx.
4. Boleh diterokai. Pensampelan rawak. Pulih dari: diterokai.com.
5. Moore, d. 2005. Statistik asas digunakan. 2. Edisi.
6. Netquest. Pensampelan rawak. Pulih dari: netquest.com.
7. Wikipedia. Sampel statistik. Diperoleh dari: dalam.Wikipedia.org