Sudut berdaftar definisi bulatan, teorem, contoh

Dia Sudut berdaftar bulatan Ia adalah yang mempunyai puncaknya pada lilitan dan separuh -pukulannya kering atau tangen yang sama. Akibatnya sudut berdaftar akan selalu cembung atau rata.

Dalam Rajah 1, beberapa sudut yang didaftarkan di lingkaran masing -masing diwakili. Sudut ∠EDF didaftarkan dengan mempunyai puncaknya pada lilitan dan dua separuh recrengers [OF) dan [df) mengeringkan lilitan. 

Rajah 1. Beberapa sudut tertulis mengenai lingkaran masing -masing. Sumber: f. Zapata dengan geogebra.

Begitu juga, sudut ∠HGI didaftarkan, kerana mempunyai puncaknya di lilitan dan sisi kering yang sama.

Sudut ∠KJR dan ∠UST juga didaftarkan dengan lilitan. Yang pertama mempunyai satu bahagian secant dan tangen yang lain, sementara yang kedua mempunyai dua sisi yang tangen ke lilitan, membentuk sudut satah rata (180º).

Beberapa penulis memanggil sudut separa yang ditimbulkan kepada orang yang mempunyai salah satu sisinya tangen ke lilitan, tetapi dalam artikel ini dia dianggap didaftarkan.

Sebarang sudut berdaftar mentakrifkan atau subtend arka yang dikaitkan dengan yang sama. Contohnya dalam Rajah 2 sudut berdaftar ∠ABC subtends arc a⌒c panjang d.

Angka yang sama menunjukkan sudut ∠DOE, yang tidak didaftarkan di lilitan kerana tidak mempunyai puncaknya pada lilitannya, tetapi di tengah atau.

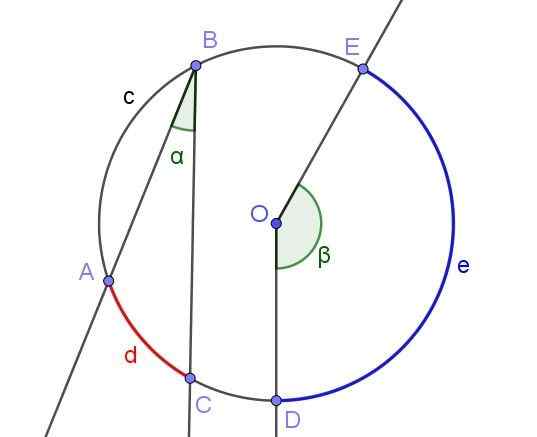Rajah 2. Sudut Berdaftar ∠ABC dan Sudut Pusat ∠DOE. Sumber: f. Zapata dengan geogebra.

[TOC]

Sudut pusat

Sebagai tambahan kepada sudut berdaftar, sudut pusat, yang merupakan puncak yang berada di tengah -tengah lilitan dan sisinya dipotong ke lilitan.

Boleh melayani anda: perbezaan antara pecahan biasa dan nombor perpuluhan

Ukuran radians sudut pusat adalah kuota antara arka yang subtends, iaitu, arka lilitan di antara sisi sudut, dan jejari lilitan.

Sekiranya lilitan adalah kesatuan (jejari 1), maka panjang arka dalam unit radio yang sama adalah ukuran sudut dalam radianes.

Dan apabila ukuran sudut diperlukan dalam darjah, maka ukurannya didarabkan dalam radian dengan faktor 180º/π.

Instrumen pengukuran sudut selalu menggunakan sudut pusat dan panjang arka yang diselaraskan oleh ini secara langsung ditentukur. Ini bermakna bahawa setiap sudut diukur, di latar belakang apa yang diukur adalah panjang arka yang disembur oleh sudut pusat.

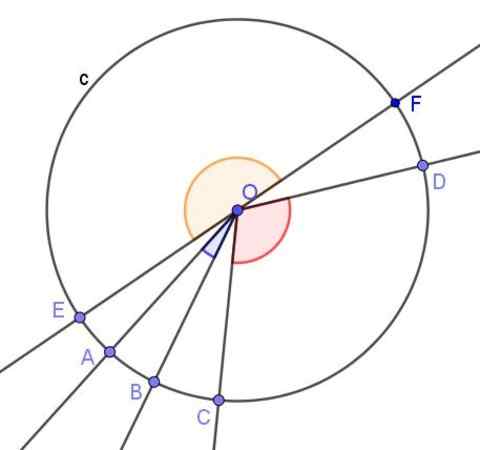Rajah 3. Beberapa sudut pusat lilitan. Sumber: f. Zapata dengan geogebra.

Teorem

- Teorem 1 (sudut berdaftar dan sudut pusat)

Ukuran sudut berdaftar adalah separuh daripada ukuran sudut pusat, jika kedua -dua sudut subtite arka yang sama.

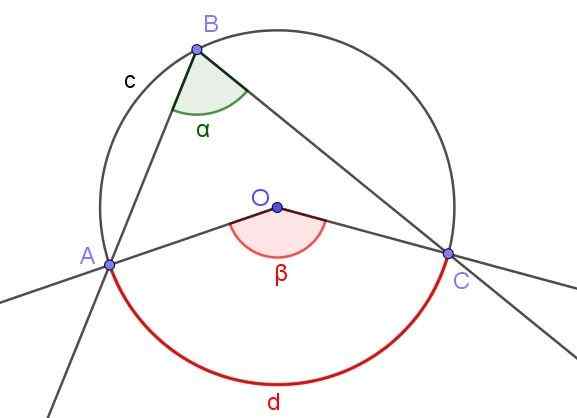Rajah 4. Sudut Berdaftar ∠ABC dan Sudut Pusat ∠AOC yang Subtite Arc A⌒C yang sama. Sumber: f. Zapata dengan geogebra.

Rajah 4 menunjukkan dua sudut ∠ABC dan ∠AOC, yang bersilang arka lingkaran yang sama.

Jika ukuran sudut berdaftar adalah α, maka ukuran β sudut pusat adalah dua kali ukuran sudut berdaftar (β = 2 α) kerana kedua -duanya menolak arka yang diukur yang sama d d.

Demonstrasi 1

Untuk menunjukkan Teorem 1, beberapa kes tertentu akan bermula, sehingga mencapai kes umum.

Boleh melayani anda: Undang -undang sandwic: penjelasan dan latihan

Katakan sudut berdaftar, di mana salah satu sisinya melewati pusat lilitan, seperti yang ditunjukkan dalam Rajah 5.

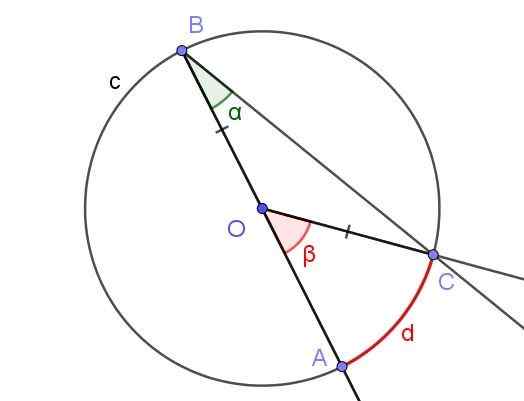Rajah 5. Sudut Berdaftar ∠ABC dengan sisi [BA) melalui O dan Sudut Pusat ∠AOC. Sumber: f. Zapata dengan geogebra.

Dalam kes ini, COB isosceles Triange terbentuk, kerana [oc] = [ob].

Dalam segitiga isosceles, sudut bersebelahan dengan asas adalah sama, oleh itu mereka perlu ∠BCO = ∠ABC = α. Sebaliknya ∠COB = 180º - β.

Memandangkan jumlah sudut dalaman segitiga cob yang anda miliki:

α + α + (180º - β) = 180º

Di mana ia mengikuti bahawa 2 α = β, atau yang setara: α = β/2. Ini bertepatan dengan apa yang Teorem 1 menyatakan: Ukuran sudut berdaftar adalah separuh daripada sudut pusat, jika kedua -dua sudut mengemukakan tali yang sama [ac].

Demonstrasi 1b

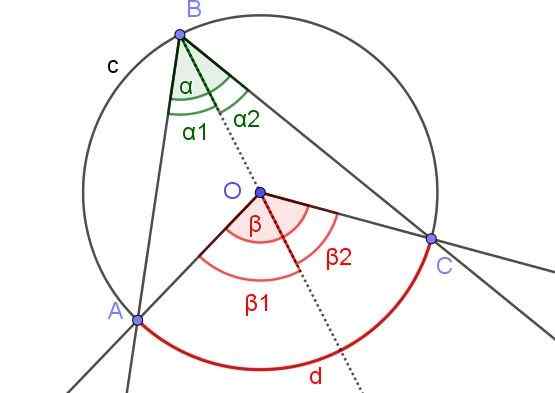Rajah 6. Pembinaan tambahan untuk menunjukkan bahawa α = β/2. Sumber: f. Zapata dengan geogebra.

Dalam kes ini terdapat sudut tertulis ∠ABC, di mana pusat atau lilitan berada di dalam sudut.

Untuk menunjukkan Teorem 1 dalam kes ini, tambahan tambahan [BO) ditarik, sehingga terdapat dua sudut berdaftar ∠ABO dan ∠OBC bersebelahan dengan separuh -kreational.

Begitu juga mereka mempunyai sudut pusat β₁ dan β₂ bersebelahan dengan separa rekreasi. Dengan cara ini anda mempunyai situasi yang sama seperti dalam Demonstrasi 1, jadi dapat dinyatakan bahawa α₂ = β₂ /2 dan α₁ = β₁ /2. Seperti α = α₁ + α₂ dan β = β₁ + β₂ Oleh itu, terdapat α = α₁ + α₂ = β₁ /2 + β₂ /2 = (β₁ + β₂) / 2 = β / 2.

Boleh melayani anda: Jenis integral

Sebagai kesimpulan α = β / 2, yang memenuhi Teorem 1.

- Teorem 2

Sekiranya dua atau lebih sudut berdaftar subtsen arka yang sama, maka mereka mempunyai ukuran yang sama.

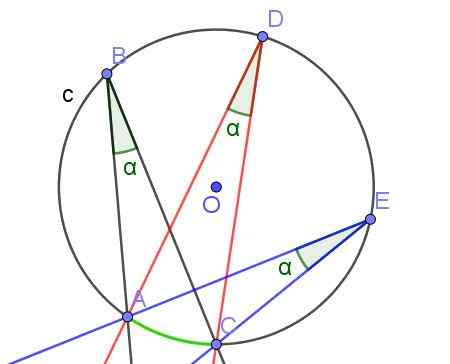Rajah 7. Sudut berdaftar yang sama ukuran α, kerana mereka subtsen arka yang sama. Sumber: f. Zapata dengan geogebra.

- Teorem 3

Subtit sudut berdaftar ada rentetan ukuran yang sama adalah sama.

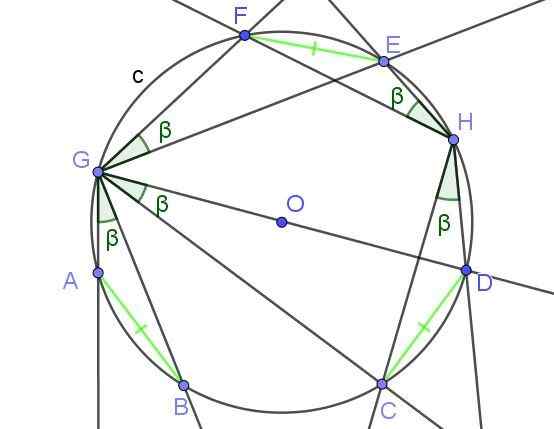Rajah 8. Sudut tertulis yang subtuse tali ukuran yang sama, mempunyai ukuran yang sama β. Sumber: f. Zapata dengan geogebra.

Contoh

- Contoh 1

Tunjukkan bahawa subit sudut tertulis diameter adalah sudut yang betul.

Penyelesaian

Sudut pusat ∠AOB yang dikaitkan dengan diameter adalah sudut rata, yang ukurannya adalah 180º.

Menurut Teorem 1, mana -mana sudut yang didaftarkan di lilitan yang subtend tali yang sama (dalam hal ini diameter), telah mengukur separuh sudut pusat yang subtite tali yang sama, yang untuk contoh kita adalah 180º/2 = 90º.

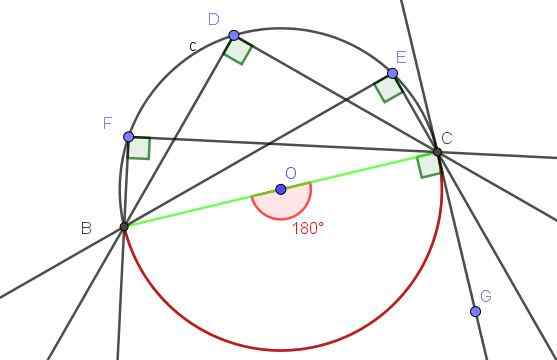Rajah 9. Sebarang sudut berdaftar yang subtend ke diameter adalah sudut yang betul. Sumber: f. Zapata dengan geogebra.

- Contoh 2

Tangen garis (bc) dalam a a ke lilitan c, menentukan sudut tertulis ∠BAC (lihat Rajah 10).

Sahkan bahawa Teorem 1 dari sudut berdaftar dipenuhi.

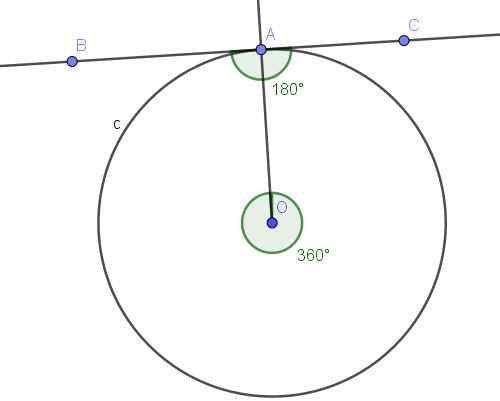Rajah 10. BAC Sudut Berdaftar dan AOA Sudut Pusat Cembungnya. Sumber: f. Zapata dengan geogebra.

Penyelesaian

Sudut ∠BAC didaftarkan kerana puncaknya berada di lilitan, dan bahagiannya [ab) dan [ac) adalah tangen ke lilitan, jadi definisi sudut tertulis dipenuhi.

Sebaliknya, sudut tertulis ∠BAC subtends gerbang a⌒a, yang merupakan lilitan lengkap. Sudut tengah yang subtend A⌒A Arch adalah sudut cembung yang ukurannya adalah sudut penuh (360º).

Subtite sudut berdaftar Arka penuh mengukur separuh daripada sudut pusat yang berkaitan, iaitu, ∠BAC = 360º/2 = 180º.

Dengan semua perkara di atas terbukti bahawa kes ini memenuhi teorem 1.

Rujukan

1. Baldor. (1973). Geometri dan trigonometri. Editorial Kebudayaan Amerika Tengah.
2. Dan. Ke. (2003). Elemen Geometri: Dengan Latihan dan Geometri Kompas. Universiti Medellin.
3. Geometry 1st. Sudut di lilitan. Pulih dari: edu.Xunta.adalah/
4. Semua sains. Cadangan Latihan sudut di lilitan. Pulih dari: Francesphysics.Blogspot.com
5. Wikipedia. Sudut berdaftar. Pulih dari: Adakah.Wikipedia.com