NULL Definisi dan Ciri -ciri, Contoh, Latihan

Dia sudut null Ia adalah ukuran yang bernilai 0, baik dalam darjah dan dalam radian atau sistem pengukuran sudut lain. Oleh itu ia tidak mempunyai amplitud atau pembukaan, seperti yang antara dua garis selari.

Walaupun definisi kedengarannya agak mudah, sudut null sangat berguna dalam banyak aplikasi fizik dan kejuruteraan, serta dalam navigasi dan reka bentuk.

Rajah 1. Antara kelajuan dan percepatan kereta ada sudut null, oleh itu kereta berjalan lebih cepat dan lebih cepat. Sumber: Wikimedia Commons.

Terdapat kuantiti fizikal yang mesti diselaraskan selari untuk mencapai kesan tertentu: jika kereta bergerak terus di lebuh raya dan antara vektor lajunya v dan pecutan vektornya ke Ada 0º, kereta semakin meningkat.

Dalam angka berikut pelbagai jenis sudut muncul termasuk sudut null ke kanan. Seperti yang dapat dilihat, sudut 0 tidak mempunyai amplitud atau pembukaan.

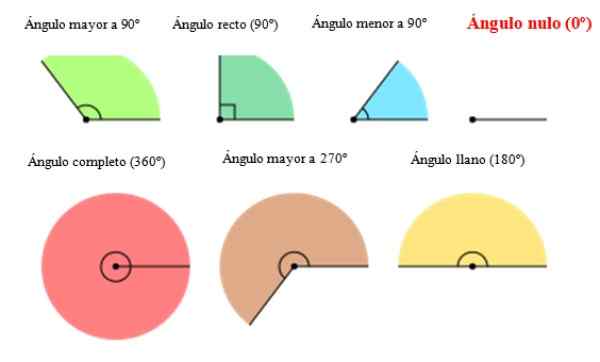Rajah 2. Jenis sudut, termasuk sudut null. Sumber: Wikimedia Commons. ORIAS [CC BY-SA (https: // creativeCommons.Org/lesen/by-sa/3.0)].[TOC]

Contoh sudut null

Diketahui bahawa garis selari membentuk sudut null. Apabila anda mempunyai garis mendatar, ini selari dengan x -axis sistem koordinat Cartesian, oleh itu kecenderungannya berkenaan dengan 0. Dengan kata lain, garis mendatar mempunyai cerun sifar.

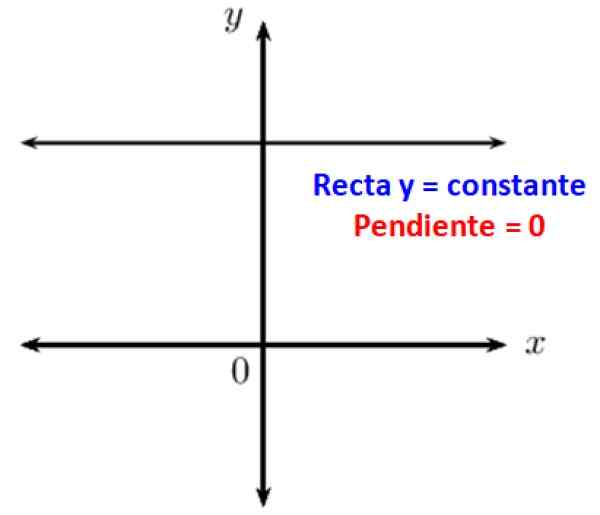Rajah 3. Garis mendatar mempunyai sifar yang belum selesai. Sumber: f. Zapata.

Juga alasan trigonometri sudut null adalah 0, 1 atau tak terhingga. Oleh itu sudut null hadir dalam banyak situasi fizikal yang melibatkan operasi dengan vektor. Sebab -sebab ini adalah:

Boleh melayani anda: pasangan teratur

-Sen 0º = 0

-cos 0º = 1

-TG 0º = 0

-SEC 0º = 1

-Bahaya 0º → ∞

-CTG 0º → ∞

Dan mereka berguna untuk menganalisis beberapa contoh situasi di mana kehadiran sudut null memainkan peranan asas:

- Kesan sudut null pada magnitud fizikal

Jumlah vektor

Apabila dua vektor selari, sudut di antara mereka adalah batal, seperti yang dilihat dalam Rajah 4 di atas. Dalam kes ini, jumlah kedua -duanya dijalankan dengan meletakkan satu demi satu dan magnitud jumlah vektor adalah jumlah magnitud tambahan (Rajah 4b).

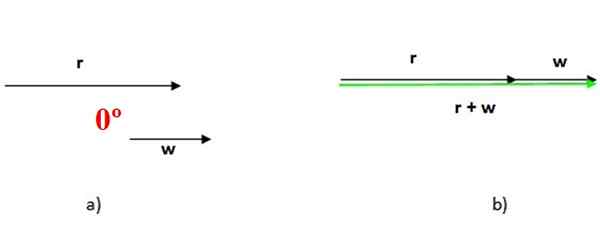Rajah 4. Jumlah vektor selari, dalam hal ini sudut di antara mereka adalah sudut null. Sumber: f. Zapata.

Apabila dua vektor selari, sudut di antara mereka adalah batal, seperti yang dilihat dalam Rajah 4 di atas. Dalam kes ini, jumlah kedua -duanya dijalankan dengan meletakkan satu demi satu dan magnitud jumlah vektor adalah jumlah magnitud tambahan (Rajah 4b)

Tork atau tork

Tork atau tork menyebabkan putaran badan. Ia bergantung pada magnitud daya yang digunakan dan bagaimana ia terpakai. Contoh yang sangat mewakili adalah kunci Bahasa Inggeris dari angka tersebut.

Untuk mencapai kesan giliran yang terbaik, memaksa secara serentak terpakai pada pemegang kunci, sama ada naik atau turun, tetapi putaran tidak dijangka jika daya selari dengan pemegang.

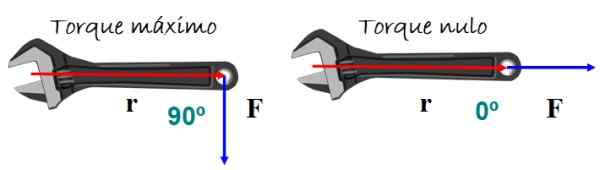Rajah 5. Apabila sudut antara kedudukan dan vektor kekuatan tidak sah, tork tidak berlaku dan oleh itu tidak ada kesan giliran. Sumber: f. Zapata.

Matematik tork τ Ia ditakrifkan sebagai vektor atau produk silang antara vektor r (vektor kedudukan) dan F (Vektor daya) Rajah 5:

Boleh melayani anda: cawangan statistik

τ = r x F

Besarnya tork adalah:

τ = r f sen θ

Menjadi θ sudut antara r dan F. Apabila dosa θ = 0 tork tidak sah, dalam hal itu θ = 0º (atau juga 180º).

Aliran medan elektrik

Aliran medan elektrik adalah magnitud skalar yang bergantung kepada intensiti medan elektrik serta orientasi permukaan di mana ia melintasi.

Dalam Rajah 6 terdapat permukaan bulat kawasan A yang mana garis medan elektrik berlalu Dan. Orientasi permukaan diberikan oleh vektor biasa n. Di sebelah kiri medan dan vektor biasa membentuk seorang pelakon sudut sewenang -wenang θ, di pusat mereka membentuk sudut null dan haknya berserenjang.

Bila Dan dan n Mereka berserenjang, garis medan tidak menyeberangi permukaan dan oleh itu alirannya sifar, sementara ketika sudut antara Dan dan n Ia tidak sah, garisan sepenuhnya melintasi permukaan.

Menandakan aliran medan elektrik oleh huruf Yunani φ (berbunyi "fi"), definisi untuk medan seragam seperti dalam angka, ia tetap seperti ini:

Φ = Dan•nKe

Titik di tengah -tengah kedua -dua vektor menandakan titik atau produk skalar, yang secara bergantian mentakrifkan:

Φ = Dan•nA = EACOSθ

Bold dan anak panah di atas surat adalah sumber untuk membezakan antara vektor dan magnitudnya, yang dilambangkan dengan huruf biasa. Oleh kerana cos 0 = 1, alirannya adalah maksimum ketika Dan dan n Mereka selari.

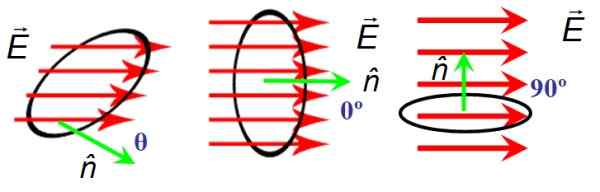Rajah 6. Aliran medan elektrik bergantung pada orientasi antara permukaan dan medan elektrik. Sumber: f. Zapata.

Latihan

- Latihan 1

Dua pasukan P dan Q Mereka bertindak serentak pada objek tepat pada masanya, kedua -dua pasukan pada mulanya membentuk sudut θ di antara mereka. Apa yang berlaku kepada magnitud daya yang terhasil apabila θ berkurangan sehingga dibatalkan?

Boleh melayani anda: Penilaian fungsi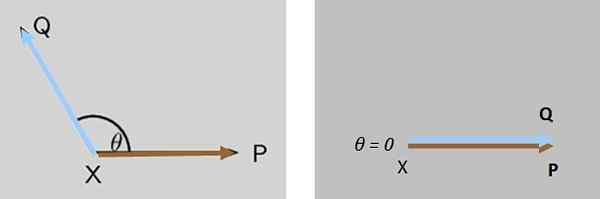 Rajah 7. Sudut antara dua daya yang bertindak pada badan berkurangan sehingga magnitud daya yang dihasilkan memperoleh nilai maksimumnya dibatalkan dalam kes ini. Sumber: f. Zapata.

Penyelesaian

Magnitud daya yang terhasil Q + P Secara beransur -ansur meningkat sehingga maksimum ketika Q dan P Mereka benar -benar selari (Rajah 7 betul).

- Latihan 2

Nyatakan sama ada sudut null adalah penyelesaian persamaan trigonometri berikut:

cos 2x = 1 + 4se x

Penyelesaian

Persamaan trigonometri adalah salah satu di mana yang tidak diketahui adalah sebahagian daripada hujah alasan trigonometri. Untuk menyelesaikan persamaan yang dicadangkan, ia adalah mudah untuk menggunakan formula untuk cosine sudut berganda:

cos 2x = cos² X - sen² x

Kerana dengan cara ini, hujah di sebelah kiri menjadi x bukan 2x. Jadi:

cos² X - sen² x = 1 + 4sen x

Sebaliknya Cos² X + sen² x = 1, jadi:

cos² X - sen² x = cos² X + sen² x + 4sen x

Istilah cos² x dibatalkan dan kekal:

- Sen² x = sen² x + 4sen x → - 2sen² x - 4senx = 0 → 2sen² x + 4senx = 0

Sekarang perubahan pembolehubah seterusnya dibuat: senx = u dan persamaannya berubah menjadi:

2U² + 4U = 0

2U (u+4) = 0

Penyelesaiannya adalah: u = 0 dan u = -4. Mengembalikan perubahan kita akan mempunyai dua kemungkinan: sin x = 0 dan senx = -4. Penyelesaian terakhir ini tidak berdaya maju, kerana payudara mana -mana sudut antara -1 dan 1, jadi kita ditinggalkan dengan alternatif pertama:

dosa x = 0

Oleh itu x = 0º adalah penyelesaian, tetapi juga berfungsi mana -mana sudut yang sinus adalah 0, yang juga boleh menjadi 180º (π radian), 360º (2 π radians) dan negatif masing -masing juga.

Penyelesaian yang paling umum mengenai persamaan trigonometri ialah: x = kπ di mana k = 0, ± 1, ± 2, ± 3, .. . k nombor integer.

Rujukan

1. Baldor, a. 2004. Geometri rata dan ruang dengan trigonometri. Penerbitan Kebudayaan s.Ke. daripada c.V. Mexico.
2. Figueroa, d. (2005). Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 3. Sistem zarah. Diedit oleh Douglas Figueroa (USB).
3. Figueroa, d. (2005). Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 5. Interaksi elektrik. Diedit oleh Douglas Figueroa (USB).
4. Onlinemathlearning. Jenis sudut. Diperolehi daripada: onlinemathlearning.com.
5. Zill, d. 2012. Algebra, trigonometri dan geometri analisis. McGraw Hill Inter -American.