Panjang tali (geometri), teorem dan latihan

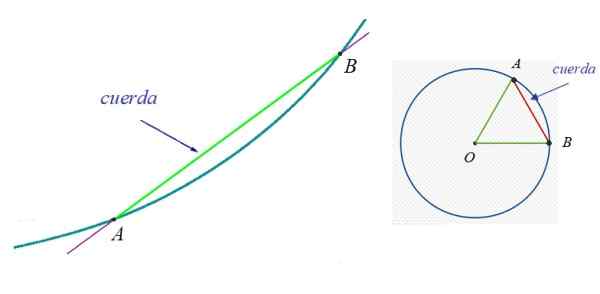
A Tali, Dalam geometri rata, ia adalah segmen garis yang menyertai dua mata dari lengkung. Dikatakan bahawa garis yang mengandungi segmen ini adalah garis pengeringan ke lengkung. Selalunya lilitan, tetapi anda pasti dapat menarik rentetan ke banyak lengkung lain, seperti elips dan perumpamaan.

Dalam Rajah 1 ke kiri terdapat lengkung, yang mana titik A dan B tergolong. Tali antara a dan b adalah segmen hijau. Di sebelah kanan adalah lilitan dan salah satu rentetan mereka, kerana mungkin untuk mengesan tak terhingga.

Rajah 1. Di sebelah kiri tali lengkung sewenang -wenangnya dan ke kanan tali bulatan. Sumber: Wikimedia Commons.

Di lilitan diameternya sangat menarik, yang juga dikenali sebagai Tali utama. Ia adalah tali yang selalu mengandungi pusat lilitan dan mengukur dua kali jejari.

Angka berikut diwakili oleh jejari, diameter, tali dan juga arka bulatan. Mengenal pasti setiap satu adalah penting apabila menyelesaikan masalah.

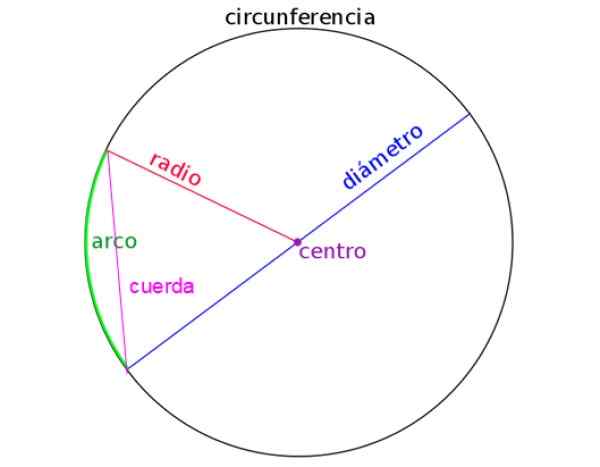Rajah 2. Unsur -unsur lilitan. Sumber: Wikimedia Commons.

[TOC]

Panjang tali lilitan

Kita boleh mengira panjang tali dalam bulatan bermula dari Rajah 3a dan 3b. Perhatikan bahawa segitiga sentiasa dibentuk dengan dua sisi yang sama (isosceles): segmen OA dan OB, yang mengukur r, jejari lilitan. Bahagian ketiga segitiga adalah segmen AB, yang dipanggil C, yang tepatnya panjang tali.

Adalah perlu untuk melukis garis serenjang ke tali c untuk bisect pada sudut θ yang wujud antara kedua -dua radio dan puncaknya adalah pusat atau lilitan. Ini adalah sudut pusat -Kerana puncaknya adalah pusat- dan garis bisektor juga merupakan secantas ke lilitan.

Ia dapat melayani anda: sifat radikal

Segera dua segi empat tepat terbentuk, yang hipotenanya. Sejak bisektor, dan dengan itu diameter, membahagikan kepada dua bahagian yang sama dengan tali, ternyata salah satu kaki adalah separuh daripada C, seperti yang ditunjukkan dalam Rajah 3b.

Dari definisi payudara sudut:

dosa (θ/2) = bertentangan/hypotenusa cateto = (c/2)/r

Oleh itu:

dosa (θ/2) = c/2r

C = 2R Sen (θ/2)

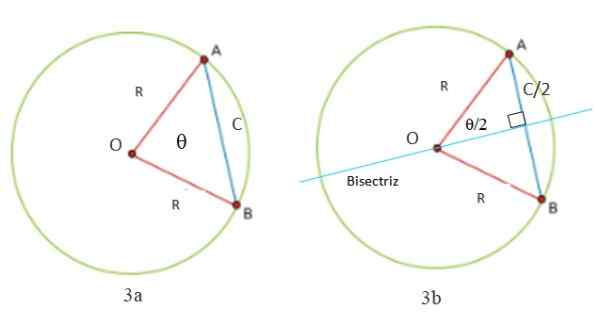Rajah 3. Segitiga yang dibentuk oleh dua radio dan tali lilitan adalah isosceles (Rajah 3), kerana ia mempunyai dua sisi sama. Bisektor membahagikannya kepada dua segi empat segi empat tepat (Rajah 3b). Sumber: Disediakan oleh f. Zapata.

Teorem String 

Teorem rentetan mengatakan:

Jika mana -mana dua tali bersilang pada satu titik, produk panjang segmen yang muncul di salah satu rentetan, adalah sama dengan produk panjang segmen yang ditakrifkan dalam tali yang lain.

Angka berikut menunjukkan dua rentetan lilitan yang sama: ab dan cd, yang bersilang pada titik p. Di tali AB, segmen AP dan PB ditakrifkan, manakala CP dan PD ditakrifkan dalam tali CD. Kemudian, mengikut teorem:

Ap . Pb = cp . P.S

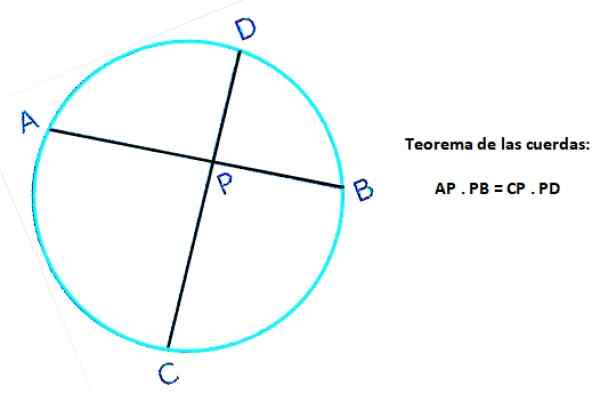Rajah 4. Teorem tali lilitan. Sumber: f. Zapata.

Latihan rentetan yang diselesaikan

- Latihan 1

Bulatan mempunyai tali 48 cm, iaitu 7 cm dari pusat. Kirakan kawasan bulatan dan perimeter lilitan.

Penyelesaian  

Untuk mengira lingkaran kawasan, sudah cukup untuk mengetahui jejari lilitan ke dataran, kerana ia dipenuhi:

A = π.R²

Sekarang, angka yang dibentuk dengan data yang disediakan adalah segitiga segi empat tepat, yang kaki masing -masing 7 dan 24 cm.

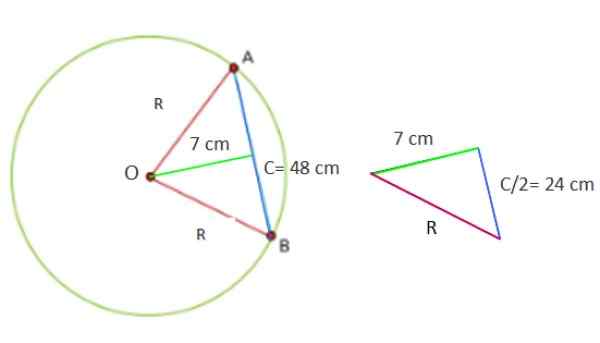Rajah 5. Geometri untuk latihan yang diselesaikan 1. Sumber: f. Zapata.

Oleh itu untuk mencari nilai r² Teorem Pythagoras C digunakan secara langsung² = a² + b², Oleh kerana R adalah hipotenus segitiga:

Boleh melayani anda: sudut null: definisi dan ciri, contoh, latihan

R² = (7 cm)² + (24 cm)² = 625 cm²

Maka kawasan yang diminta adalah:

A = π. 625 cm² = 1963.5 cm²

Bagi perimeter atau panjang l lilitan, ia dikira oleh:

L = 2π. R

Mengganti Nilai:

R = √625 cm² = 25 cm

L = 2π. 25 cm = 157.1 cm.

- Latihan 2

Tentukan panjang tali bulatan yang persamaannya:

x² + dan² - 6x - 14y -111 = 0

Adalah diketahui bahawa koordinat titik tengah tali adalah p (17/2; 7/2).

Penyelesaian

Titik tengah tali p tidak tergolong dalam lilitan, tetapi titik melampau tali ya. Masalahnya dapat diselesaikan melalui teorem rentetan yang dinyatakan sebelum ini, tetapi pertama -tama ia mudah.

Langkah 1: Dapatkan persamaan kanonik lilitan

Persamaan kanonik lilitan dengan pusat (h, k) adalah:

(X-h)² + (Y-K)² = R²

Untuk mendapatkannya, adalah perlu untuk melengkapkan kotak:

(x² - 6x) + (dan² - 14y) -111 = 0

Perhatikan bahawa 6x = 2.(3x) dan 14y = 2.(7y), supaya ungkapan sebelumnya ditulis semula, tidak berubah:

(x² - 6x+3²-3²) + (dan² - 14y+7²-7²) -111 = 0

Dan sekarang, ingat definisi produk terkenal (A-B)² = a² - 2ab + b² Ia boleh ditulis:

(X - 3)² - 3² + (dan - 7)² - 7² - 111 = 0

= (x - 3)² + (dan - 7)² = 111 + 3² + 7² → (x - 3)² + (dan - 7)² = 169

Lingkaran mempunyai pusat (3.7) dan radio r = √169 = 13. Angka berikut menunjukkan graf lilitan dan rentetan yang akan digunakan dalam teorem:

Boleh melayani anda: Apakah 7 elemen lilitan?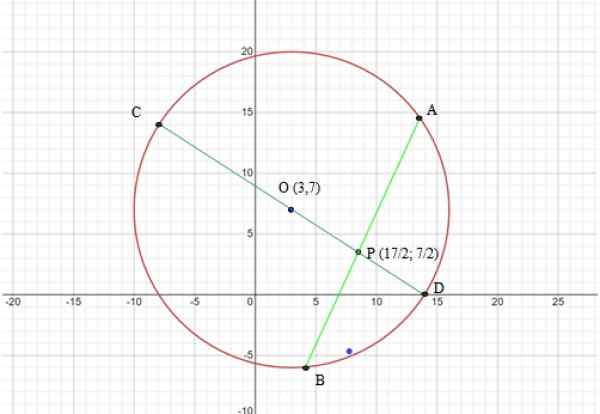Rajah 6. Grafik lilitan latihan diselesaikan 2. Sumber: f. Zapata melalui Mathway Kalkulator Grafik Dalam Talian.

Langkah 2: Tentukan segmen yang akan digunakan dalam teorem rentetan

Segmen yang akan digunakan adalah rentetan CD dan AB, menurut Rajah 6, kedua -duanya dipotong pada titik p, oleh itu:

Cp . PD = AP. Pb

Sekarang kita akan mencari jarak antara titik o dan p, kerana ini akan memberi kita panjang segmen op. Sekiranya kita menambah jejari panjang ini, kita akan mempunyai segmen CP.

Jarak d_Op Antara dua titik koordinat (x₁,dan₁) dan (x₂,dan₂) adalah:

d_Op² = Op² = (x₂ - x₁)² + (dan₂ - dan₁)² = (3- 17/2)² + (7-7/2)² = 121/4 + 49/4 = 170/4

d_Op = OP = √170 /2

Dengan semua hasil yang diperoleh, ditambah dengan graf, kami membina senarai segmen berikut (lihat Rajah 6):

Co = 13 cm = r

OP = √170 /2 cm

Cp = op + r = 13 + √170 /2 cm

PD = OD - OP = 13 - √170 /2 cm

AP = pb

2.AP = panjang tali

Menggantikan teorem rentetan:

Cp . PD = AP . PB = [(13 +√170/2) . (13 -√170 /2)] = AP²

[169-170/4] = AP²

253/2 = AP²

AP = √ (253/2)

Panjang tali adalah 2.AP = 2 (√253/2) = √506

Bolehkah pembaca menyelesaikan masalah dengan cara lain?

Rujukan

1. Baldor, a. 2004. Geometri rata dan ruang dengan trigonometri. Penerbitan Kebudayaan s.Ke. daripada c.V. Mexico.
2. C-K12. Lenght dari kord. Pulih dari: ck12.org.
3. Escobar, j. Lilitan. Pulih dari: matematik.Anda.Edu.co.
4. Villena, m. Conical. Diperolehi dari: DSPACE.Espol.Edu.Ec.
5. Wikipedia. Tali (Geometri). Pulih dari: Adakah.Wikipedia.org.