Penerangan, Aplikasi, Contoh dan Latihan Teorem Norton

Dia Teorem Norton, yang terpakai kepada litar elektrik, menetapkan bahawa litar linear dengan dua terminal A dan B, boleh digantikan dengan satu lagi setaraf sepenuhnya, yang terdiri daripada sumber semasa yang dipanggil i_Tidak disambungkan selari dengan rintangan r_Tidak.

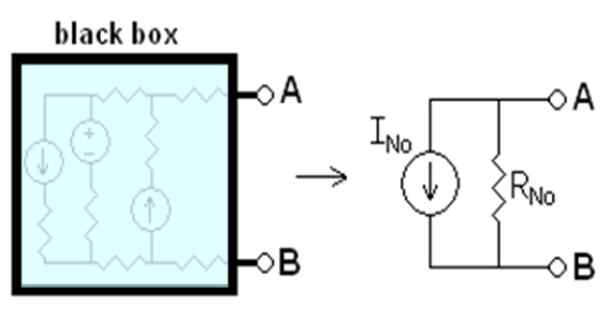
Kata semasa i_Tidak saya dengar_N Ia adalah yang akan mengalir di antara titik a dan b, jika mereka pendek. Rintangan r_N Ia adalah rintangan yang setara antara terminal, apabila semua sumber bebas dinyahaktifkan. Semuanya dikatakan dijangka dalam Rajah 1.

Rajah 1. Litar setara Norton. Sumber: Wikimedia Commons. Drumkid [CC BY-SA 3.0 (http: // creativeCommons.Org/lesen/by-sa/3.0/]]

Kotak hitam dalam angka mengandungi litar linear yang akan digantikan dengan setara Norton. Litar linear adalah satu di mana input dan output mempunyai pergantungan linear, seperti hubungan antara voltan v dan arus langsung i dalam elemen ohmic: v = i.R.

Ungkapan ini sepadan dengan undang -undang ohm, di mana r adalah rintangan, yang juga boleh menjadi impedans, jika ia adalah litar semasa berselang.

Teorem Norton dibangunkan oleh jurutera elektrik dan pencipta Edward L. Norton (1898-1983), yang bekerja lama untuk Laboratorium Bell.

[TOC]

Aplikasi Teorem Norton

Apabila mereka mempunyai rangkaian yang sangat rumit, dengan banyak rintangan atau impedans dan anda mahukan litar yang lebih kecil dan lebih mudah diurus.

Dengan cara ini, teorem Norton sangat penting ketika merancang litar dengan pelbagai elemen, serta mengkaji tindak balas mereka.

Hubungan antara teorem Norton dan Thevenin

Teorem Norton adalah teorem dwi thevenin, yang bermaksud mereka bersamaan. Teorem Thevenin menunjukkan bahawa kotak hitam dalam Rajah 1 dapat digantikan dengan sumber voltan siri dengan rintangan, yang dipanggil rintangan thevenin r_Th. Ini dinyatakan dalam angka berikut:

Boleh melayani anda: Mekanik Bahan: Sejarah, Bidang Pengajian, Aplikasi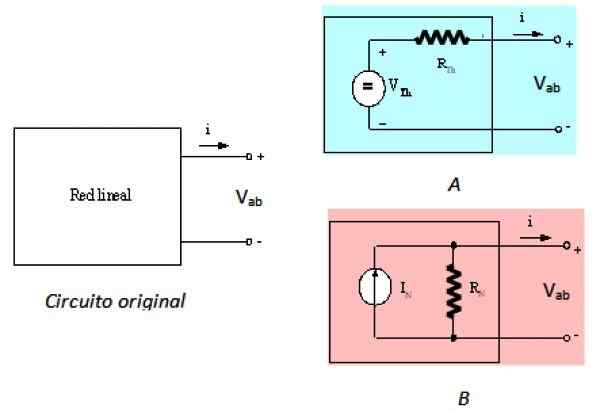 Rajah 2. Litar kiri asal, dan kesamaannya dari Thévenin dan Norton. Sumber: f. Zapata.

Litar kiri adalah litar asal, rangkaian linear dalam kotak hitam, litar ke kanan adalah bersamaan dengan thevenin dan litar B Ia bersamaan dengan Norton, seperti yang diterangkan. Dilihat dari terminal A dan B, ketiga litar adalah bersamaan.

Sekarang perhatikan bahawa:

-Dalam litar asal ketegangan antara terminal adalah v_Ab.

-V_Ab  = V_Th Dalam litar Ke

-Akhirnya, v_Ab  = I_N.R_N Dalam litar B

Sekiranya terminal A dan B adalah litar pintas dalam tiga litar, ia mesti dipenuhi bahawa voltan dan arus di antara titik -titik ini mestilah sama untuk ketiga -tiga, kerana mereka bersamaan. Jadi:

-Dalam litar asal arus adalah i.

-Untuk litar A, arus ialah i = v_Th / R_Th, Menurut undang -undang ohm.

-Akhirnya dalam litar b, arus adalah i_N

Oleh itu, disimpulkan bahawa rintangan Norton dan Thevenin mempunyai nilai yang sama, dan arus diberikan oleh:

i = i_N = V_Th / R_Th = V_Th / R_N

Contoh

Untuk menggunakan teorem Norton dengan betul, langkah -langkah berikut diikuti:

-Bahagian litar yang setara Norton akan dijumpai dari rangkaian adalah mengasingkan dari rangkaian.

-Dalam litar yang tinggal, tunjukkan terminal a dan b.

-Gantikan sumber voltan dengan litar pintas dan yang terkini dengan litar terbuka, untuk mencari rintangan bersamaan antara terminal a dan b. Ini r_N.

-Kembalikan semua sumber ke kedudukan asalnya, pendek -circuit terminal a dan b dan cari arus yang beredar di antara mereka. Ini adalah saya_N.

Boleh melayani anda: Kesan Doppler: Keterangan, Formula, Kes, Contoh

-Lukis litar bersamaan Norton mengikut apa yang ditunjukkan dalam Rajah 1. Kedua -duanya, sumber semasa dan rintangan bersamaan selari.

Anda juga boleh memohon teorem Thevenin untuk mencari r_Th, bahawa kita sudah tahu sama dengan r_N, Kemudian oleh undang -undang ohm anda dapat mencari i_N Dan litar yang dihasilkan ditarik.

Dan sekarang mari kita lihat contoh:

Cari bersamaan Norton antara titik A dan B litar berikut:

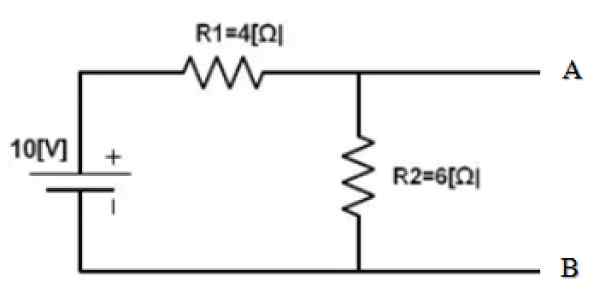Rajah 3. Contoh litar. Sumber: f. Zapata.

Bahagian litar sudah diasingkan yang setarafnya mesti dijumpai. Dan mata a dan b jelas ditentukan. Apa yang berikut ialah litar pintas sumber 10 V dan dapatkan rintangan yang setara dengan litar yang diperoleh:

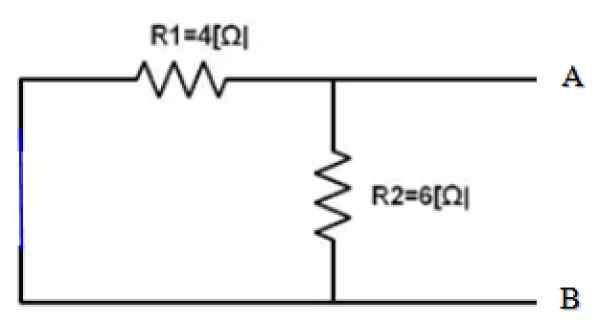Rajah 4. Sumber pendek -sirkuit. Sumber: f. Zapata.

Pandangan dari terminal a dan b, kedua -dua rintangan r r₁ dan r₂ Oleh itu, mereka selari:

1/r_Pers = 1/r₁₂ = (1/4) + (1/6) Ω^-1 = 5/12 Ω^-1  → R_Pers = 12/5 Ω = 2.4 Ω

Maka sumbernya dikembalikan ke tempatnya dan titik A dan B adalah litar pendek untuk mencari arus yang beredar di sana, ini akan menjadi_N. Kalau macam itu:

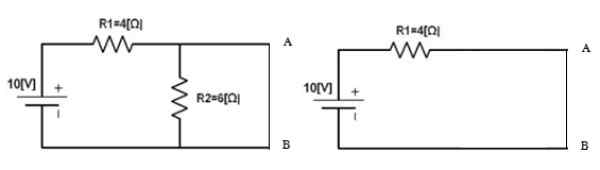Rajah 5. Litar untuk mengira arus Norton. Sumber: f. Zapata.

Yo_N = 10 v / 4 Ω = 2.5 a

Setara Norton

Akhirnya, setara Norton dengan nilai -nilai yang ditemui ditarik:

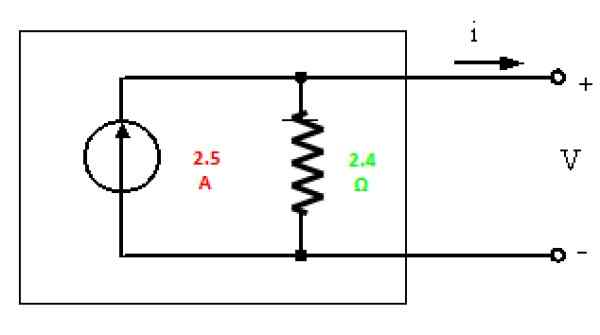Rajah 6. Norton bersamaan dengan litar dalam Rajah 3. Sumber: f. Zapata.

Latihan diselesaikan

Dalam litar angka berikut:

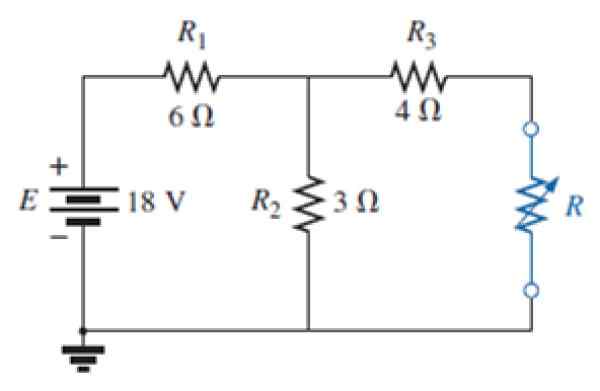Rajah 7. Litar untuk latihan diselesaikan. Sumber: Alexander, C. 2006. Asas Litar Elektrik. Ke -3. Edisi. MC Graw Hill.

a) Cari litar setara Norton rangkaian rintangan biru luar.

b) Juga cari setaraf Thévenin.

Penyelesaian kepada

Berikutan langkah -langkah yang ditunjukkan di atas, sumber mestilah pendek -Circuit:

Boleh melayani anda: Pembedahan bunyi: Apa yang terdiri daripada contoh, aplikasi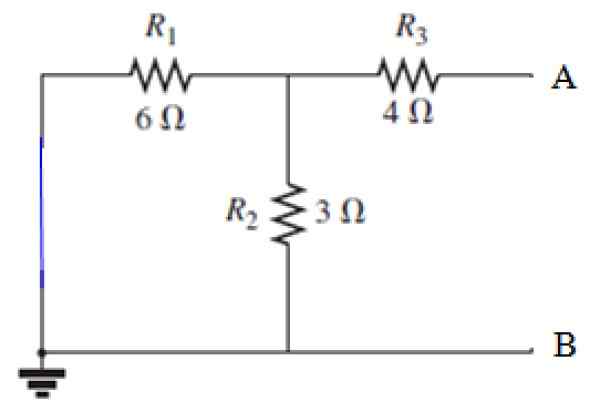 Rajah 8. Sumber pendek -sirkuit dalam litar dalam Rajah 7. Sumber: f. Zapata.

Pengiraan RN

Lihat dari terminal a dan b, rintangan r₃ dalam siri dengan selari yang dibentuk oleh rintangan r r₁ dan r₂, Mari kita mula -mula mengira rintangan bersamaan selari ini:

1/r₁₂ = (1/6)+ (1/3) Ω^-1 = 1/2 Ω^-1  → R_Pers = 2/1 Ω = 2Ω

Dan kemudian selari ini bersiri dengan r_3, supaya rintangan yang setara adalah:

R_Pers = 2 Ω + 4 Ω = 6 Ω

Inilah nilai kedua -kedua r_N Sehingga r_Th, seperti yang dijelaskan sebelumnya.

Pengiraan dalam

Kemudian terminal A dan B adalah litar pendek, mengembalikan sumber ke tempatnya:

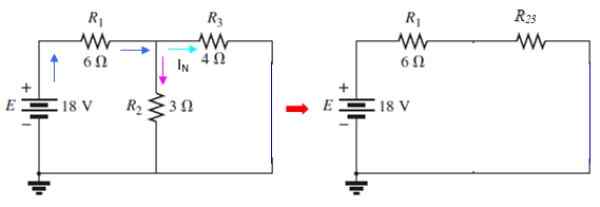Rajah 9. Litar Semasa Norton. Sumber: f. Zapata.

Semasa melewati i₃ adalah semasa i_N dicari, yang boleh ditentukan dengan kaedah mesh atau menggunakan siri dan selari. Dalam litar ini r₂ dan r₃ Mereka selari:

1/r₂₃ = (1/3)+ (1/4) Ω^-1 = 7/12 Ω^-1  → R₂₃ = 12/7 Ω

Rintangan r₁ Ia bersiri dengan selari ini, maka:

R₁₂₃ = 6 + (12/7) Ω = 54/7 Ω

Semasa yang keluar dari sumber (warna biru) dikira oleh undang -undang ohm:

V = i. R → i = v/r = 18 v/(54/7 Ω) = 7/3 a

Arus ini dibahagikan kepada dua bahagian: satu yang melintasi r₂ Dan satu lagi yang melintasi r₃. Walau bagaimanapun, arus yang melintasi r selari₂₃ Ia sama yang melalui r₁, Seperti yang dapat dilihat dalam litar pertengahan angka. Voltan ada:

V₂₃ = I.R₂₃ = (7/3) a .(12/7) Ω = 4 v

Kedua -dua rintangan r₂ dan r₃ Mereka berada di voltan itu, kerana mereka selari, oleh itu:

Yo₃ = V₂₃ / R₃ = 4 v / 4 Ω = 1 a

Kami sudah mencari arus Norton, kerana seperti yang dikatakan sebelumnya i₃ = I_N, Jadi:

Yo_N = 1 a

Setara Norton

Segala -galanya siap untuk menarik Norton bersamaan litar ini antara titik a dan b:

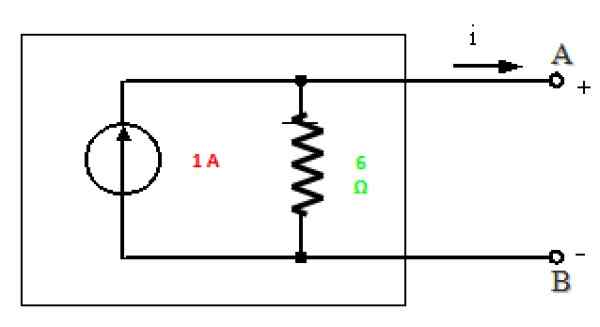Rajah 10. Norton bersamaan dengan litar dalam Rajah 7. Sumber: f. Zapata.

Penyelesaian b

Mencari bersamaan Thévenin sangat mudah, kerana r_Th = R_N= 6 Ω dan seperti yang dijelaskan dalam bahagian sebelumnya:

V_Th = I_N. R_N = 1 a . 6 Ω = 6 v

Litar bersamaan Thévenin adalah:

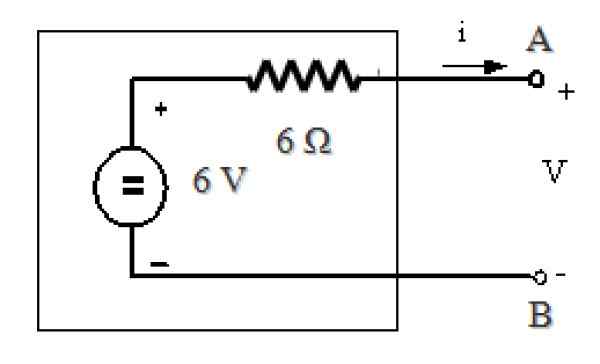Rajah 11. Setara dengan litar thevenin dalam Rajah 7. Sumber: f. Zapata.

Rujukan

1. Alexander, c. 2006. Asas Litar Elektrik. Ke -3. Edisi. MC Graw Hill.
2. Boylestad, r. 2011. Pengenalan kepada Analisis Litar. 2. Edisi. Pearson.
3. Dorf, r. 2006. Pengenalan kepada litar elektrik. Ke -7. Edisi. John Wiley & Sons.
4. Edminister, j. Sembilan belas sembilan puluh enam. Litar elektrik. Siri Schaum. Ke -3. Edisi. MC Graw Hill.
5. Wikipedia. Teorem Norton . Pulih dari: ia adalah.Wikipedia.org.