Sudut dalam jenis lilitan, sifat, latihan diselesaikan

Dipanggil Sudut lilitan kepada mereka yang mana unsur -unsurnya atau bersilang di lilitan yang diberikan. Antaranya adalah yang berikut:

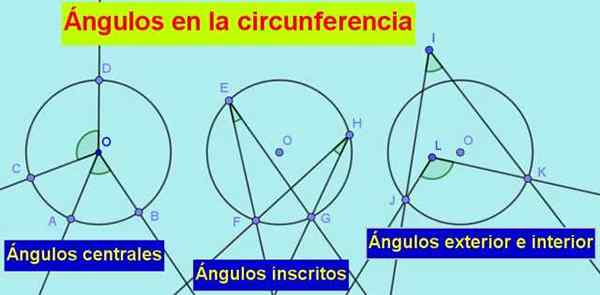
1.- Dia sudut pusat, yang puncaknya berada di tengah -tengah lilitan dan sisinya mengeringkannya, seperti yang kita lihat dalam imej berikut:

Rajah 1. Jenis sudut di lilitan adalah: pusat, yang tertulis, luaran dan pedalaman. Sumber: f. Zapata.

2.- Dia sudut berdaftar, yang puncaknya berada di lilitan dan sisinya kering atau tangen ke lilitan.

3.- Sudut luar, yang puncaknya keluar dari lilitan tetapi sisinya kering atau tangen ke lilitan.

4.- Dia Sudut dalaman, dengan puncak di dalam lilitan dan sisi kering yang sama.

Semua sudut ini menjaga hubungan tertentu antara satu sama lain dan ini membawa kita ke sifat -sifat penting antara sudut milik lilitan yang diberikan.

[TOC]

Sifat

- Sudut pusat

Sudut tengah ditakrifkan sebagai yang puncaknya berada di tengah lilitan dan sisinya dipotong ke lilitan.

Ukuran radians sudut pusat adalah kuota antara arka yang subtends, iaitu, arka lilitan di antara sisi sudut, dan jejari lilitan. 

Sekiranya lilitan adalah kesatuan, iaitu, jejari 1, maka ukuran sudut pusat adalah panjang arka, yang sepadan dengan bilangan radian.

Sekiranya anda menginginkan ukuran sudut pusat dalam darjah, maka ukurannya didarabkan dalam radian dengan faktor 180º/π.

Instrumen pengukuran sudut, seperti pengangkut dan goniometer, selalu menggunakan sudut pusat dan panjang arka subtended.

Boleh melayani anda: derivatif separa: sifat, pengiraan, latihan

Mereka dikalibrasi dalam darjah sexagesimal, yang bermaksud bahawa apabila sudut diukur dengan mereka, di belakang apa yang diukur adalah panjang arka yang disembur oleh sudut pusat.

Harta

Ukuran sudut pusat dalam radian adalah sama dengan panjang arka yang subtin atau memintas dibahagikan dengan panjang jejari.

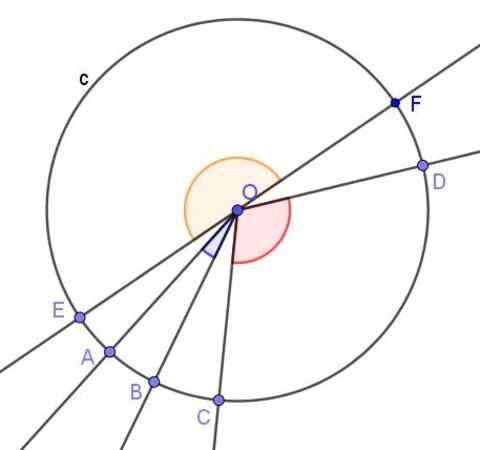Rajah 2. Tiga sudut pusat ditunjukkan. Satu akut, bodoh yang lain dan satu rata. Sumber: f. Zapata.

- Sudut berdaftar

Sudut berdaftar lilitan adalah salah satu yang mempunyai puncaknya pada lilitan dan separuh -pukulannya kering atau tangen yang sama. 

Sifatnya adalah:

Sifat

-Sudut berdaftar adalah cembung atau rata.

-Apabila sudut tertulis memintas arka yang sama dengan sudut pusat, ukuran yang pertama akan menjadi separuh daripada yang kedua.

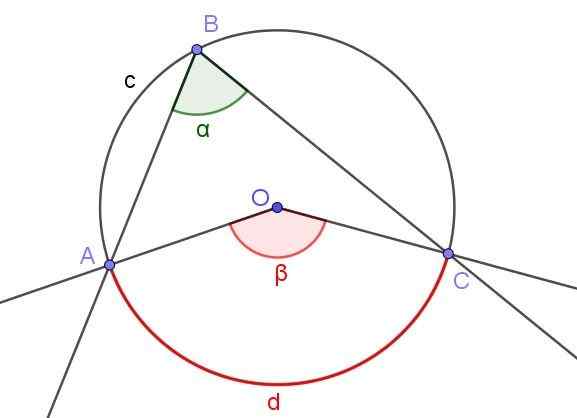Rajah 3. Sudut Berdaftar ∠ABC dan Sudut Pusat ∠AOC yang Subtite Arc A⌒C yang sama. Sumber: f. Zapata.

Rajah 3 menunjukkan dua sudut ∠ABC dan ∠AOC yang memintas arka lilitan yang sama A⌒C.

Jika ukuran sudut berdaftar adalah α, maka ukuran β sudut pusat adalah dua kali ukuran sudut berdaftar (β = 2 α) kerana kedua -duanya menolak arka yang diukur yang sama d d.

- Sudut luar

Ia adalah sudut yang puncaknya berada di luar lilitan dan setiap bahagiannya memotong ke lilitan dalam satu atau lebih mata.

Harta

-Ukurannya sama dengan separuh -ekspres (atau perbezaan dibahagikan dengan 2) sudut pusat yang memintas gerbang itu sendiri.

Untuk memastikan bahawa langkah itu positif, separuh -ekspres harus selalu menjadi sudut pusat ukuran terbesar kurang ukuran sudut pusat yang lebih rendah, seperti yang digambarkan dalam angka berikut.

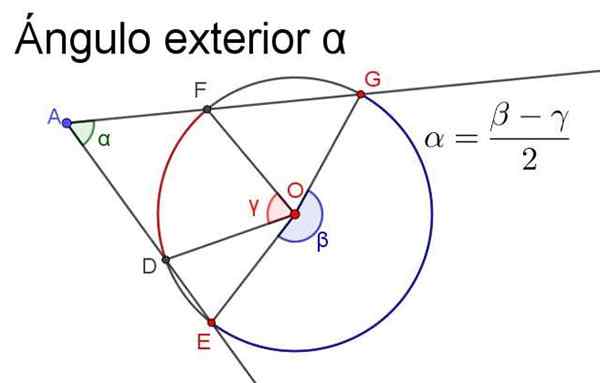Rajah 4. Sudut luar α adalah sama dengan separuh -pencegahan sentral yang subtsen gerbang yang sama. Sumber: f. Zapata.

- Sudut dalaman

Sudut dalam adalah yang puncaknya berada di dalam lilitan dan sisinya dipotong ke lilitan.

Boleh melayani anda: Koefisien penentuan: formula, pengiraan, tafsiran, contoh

Harta 

Ukurannya adalah sama dengan separuh daripada sudut pusat yang menyebarkan arka yang sama, ditambah dengan sudut pusat yang menyebarkan arka yang sama dengan sudut lanjutannya (ini adalah sudut dalaman yang dibentuk oleh pelengkap separuh ke arah yang asal sudut dalaman).

Angka berikut menggambarkan dan menjelaskan harta sudut dalaman.

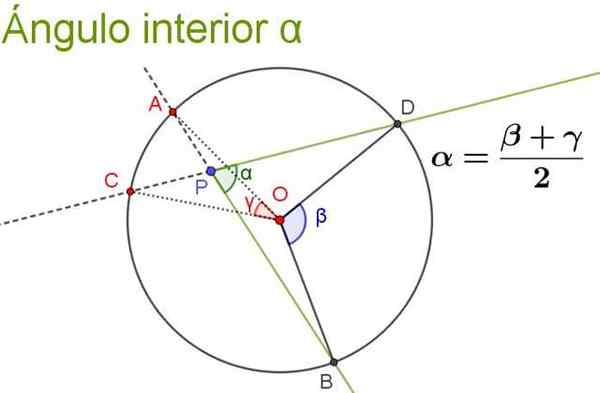Rajah 5. Sudut batin α sama dengan separuh -seismum sudut pusat yang subtsen gerbang yang sama seperti dia sendiri. Sumber: f. Zapata.

Latihan yang diselesaikan

- Latihan 1

Katakan sudut tertulis di mana salah satu sisinya melewati pusat lilitan, seperti yang ditunjukkan dalam Rajah 6. Radius lilitan adalah OA = 3 cm dan arka D mempunyai panjang π/2 cm. Tentukan nilai sudut α dan β.

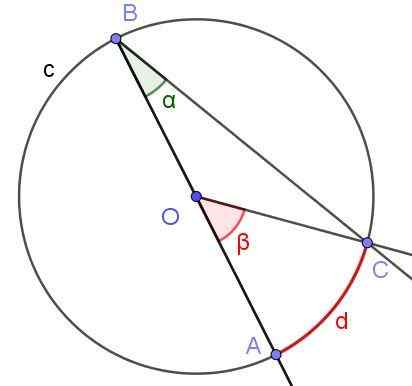Rajah 6. Sudut Berdaftar ∠ABC dengan sisi [BA) melalui O dan Sudut Pusat ∠AOC.Sumber: f. Zapata.

Penyelesaian

Dalam kes ini, COB isosceles Triange terbentuk, kerana [oc] = [ob]. Dalam segitiga isosceles, sudut bersebelahan dengan asas adalah sama, oleh itu mereka perlu ∠BCO = ∠ABC = α. Sebaliknya ∠COB = 180º - β. Memandangkan jumlah sudut dalaman segitiga cob yang anda miliki:

α + α + (180º - β) = 180º

Dari mana ia mengikuti bahawa 2 α = β, atau yang bersamaan α = β/2, yang mengesahkan harta (3) bahagian sebelumnya, bahawa ukuran sudut berdaftar adalah separuh daripada sudut pusat, apabila kedua -dua sudut tolak tali yang sama [ac].

Sekarang kita terus menentukan nilai -nilai berangka: sudut β adalah pusat dan ukurannya dalam radian adalah nisbah antara arka D dan radius r = OA, jadi ukurannya adalah:

β = d / r = (π / 2 cm) / (3 cm) = π / 6 rad = 30º.

Boleh melayani anda: Quadrilateral: Unsur, sifat, klasifikasi, contoh

Sebaliknya ia telah disahkan bahawa α = β / 2 = (π / 6 rad) / 2 = π / 12 rad = 15º. 

- Latihan 2

Dalam Rajah 7 sudut α₁ dan β₂ mempunyai ukuran yang sama. Di samping itu sudut β₁ Ia mengukur 60º. Tentukan sudut β dan α.

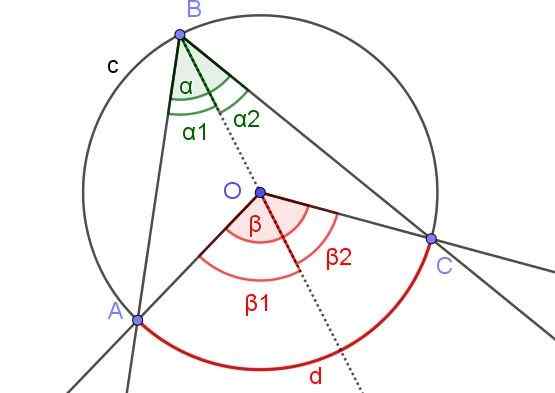Rajah 7. Dalam Rajah α₁ = β₂ dan β₁ = 60º. Tentukan nilai β dan α. Sumber: f. Zapata.

Penyelesaian

Dalam kes ini terdapat sudut tertulis ∠ABC di mana pusat atau lilitan berada di dalam sudut.

Kerana harta (3) anda mempunyai α₂ = β₂ /2 dan α₁ = β₁ /2. Sebagai:

α = α₁ + α₂ dan β = β₁ + β₂

Oleh itu, anda mempunyai:

α = α₁ + α₂ = β₁ /2 + β₂ /2 = (β₁ + β₂) / 2 = β / 2.

Iaitu, menurut sifat -sifat:

α = β / 2

Seperti yang kita diberitahu bahawa β₁ = 60º kemudian:

α₁ = β₁ / 2 = 60º / 2 = 30º.

Mereka juga memberitahu kami bahawa α₁ = β₂ Jadi ia mengikutinya:

β₂ = 30º.

Sudut β adalah:

β₁ + β₂ = 60º + 30º = 90º.

Dan sebagai α = β / 2, maka:

α = 90º / 2 = 45º. 

Kesimpulannya:

β = 90º dan α = 45º.

Rujukan

1. Baldor, a. 1973. Geometri dan trigonometri. Editorial Kebudayaan Amerika Tengah.
2. Dan. Ke. 2003. Elemen Geometri: Dengan Latihan dan Geometri Kompas. Universiti Medellin.
3. Geometry 1st. Sudut di lilitan. Pulih dari: edu.Xunta.adalah.
4. Semua sains. Latihan yang diselesaikan sudut di lilitan. Pulih dari: Francesphysics.Blogspot.com
5. Wikipedia. Sudut berdaftar. Pulih dari: Adakah.Wikipedia.com