Penjelasan keadaan keseimbangan kedua, contoh, latihan

The Keadaan keseimbangan kedua Ia menetapkan bahawa jumlah tork atau momen yang dihasilkan oleh semua daya yang bertindak ke atas badan, tanpa mengira titik apa yang dikira, mesti dibatalkan sehingga badan tersebut berada dalam keseimbangan statik atau dinamik.

Menandakan tork atau momen kekerasan melalui huruf Yunani τ, Secara matematik ia dinyatakan seperti berikut:

Σ τ = 0

Rajah 1. Untuk mengimbangi rocker, perlu menerapkan keadaan keseimbangan kedua. Sumber: Pxhere.

Surat berani menunjukkan sifat vektor pada masa ini, yang mesti dibatalkan berkenaan dengan mana -mana titik yang dipilih sebagai pusat putaran. Dengan cara ini, membatalkan tork bersih, dijamin bahawa objek tidak mula berpaling atau berpaling.

Walau bagaimanapun, jika objek sudah berputar sebelum ini, dan tork bersih hilang secara tiba -tiba, putaran akan berterusan, tetapi dengan kepantasan sudut yang berterusan.

Keadaan keseimbangan kedua digunakan bersempena dengan keadaan pertama, yang mengatakan bahawa jumlah daya pada badan mesti tidak sah, supaya ia tidak bergerak, atau jika ia berlaku, dengan pergerakan rectilinear seragam:

Σ F = 0

Kedua -dua keadaan berlaku untuk badan yang dilanjutkan, mereka yang dimensi dapat diukur. Apabila objek sepatutnya menjadi zarah, tidak masuk akal untuk bercakap mengenai putaran, dan keadaan pertama untuk menjamin keseimbangan sudah cukup.

Contoh

Keadaan keseimbangan kedua diturunkan dalam situasi yang tidak terkira banyaknya:

Semasa memanjat tangga

Semasa menyokong tangga di lantai dan dinding, kita memerlukan cukup untuk menggosok, terutamanya di lantai, untuk memastikan bahawa tangga tidak tergelincir. Sekiranya kita cuba memanjat tangga yang disokong di lantai berminyak, basah atau licin, tidak sukar untuk menjangka kita akan jatuh.

Untuk dapat menggunakan tangga dengan yakin, perlu berada dalam keseimbangan statik semasa memanjat dan ketika berada di langkah yang diperlukan.

Ia boleh melayani anda: Pluto (Planet Kerdil)

Menggerakkan almari

Apabila anda ingin memindahkan perabot yang tinggi sebagai almari, atau mana -mana bahagian yang tinggi lebih besar daripada yang luas, mudah untuk mendorong pada titik yang rendah, untuk mengelakkan terbalik, dengan cara ini lebih cenderung bahawa perabot akan meluncur sebaliknya berpaling dan berbaring.

Dalam keadaan sedemikian perabot tidak semestinya dalam keseimbangan, kerana ia boleh dipindahkan dengan cepat, tetapi sekurang -kurangnya ia tidak akan berubah.

Balkoni

Balai yang cemerlang bangunan mesti dibina menjamin bahawa, walaupun terdapat banyak orang di atas, ia tidak berubah dan runtuh.

Dielektrik dalam medan elektrik luaran

Semasa meletakkan bahan dielektrik di medan elektrik luaran, molekul bergerak dan berputar untuk mengamalkan kedudukan keseimbangan, mewujudkan medan elektrik di dalam bahan.

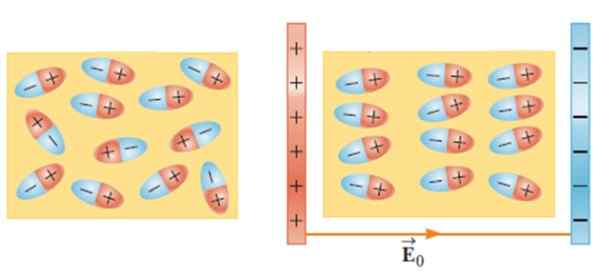Rajah 2.- Tanpa medan elektrik luaran, dipoles rawak (kiri). Medan luaran menggunakan tork pada molekul dielektrik dan ini disusun semula. Sumber: Serway, r. Fizik untuk Sains dan Kejuruteraan.

Kesan ini menjadikan kapasiti peningkatan kondensor apabila bahan seperti kaca, getah, kertas atau minyak diperkenalkan di antara perisainya.

Tanda dan lampu

Adalah biasa bagi banyak premis untuk menggantung notis di dinding bangunan, sehingga mereka dapat dilihat oleh orang yang lewat.

Poster diikat oleh bar dan kabel, kedua -duanya tetap di dinding menggunakan sokongan. Pelbagai kuasa yang bertindak mesti memastikan bahawa poster tidak jatuh, yang mana kedua -dua keadaan keseimbangan itu bertindak.

Reflektor di taman juga boleh diletakkan dengan cara ini, seperti dalam angka berikut:

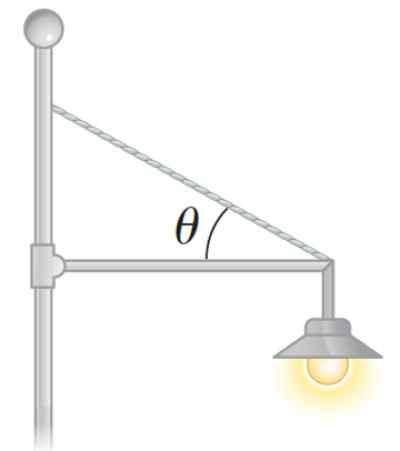Rajah 3. Lampu imbangan statik. Sumber: Serway. Fizik untuk Sains dan Kejuruteraan.

Cara mengira tork bersih atau momen bersih daya?

Tork atau momen kekerasan, dilambangkan oleh τ Sama ada M Dalam sesetengah teks, ia sentiasa dikira berkenaan dengan beberapa titik di mana paksi putaran berlalu.

Ia ditakrifkan sebagai produk vektor antara vektor kedudukan r, yang diarahkan dari paksi tersebut ke titik permohonan kekuatan dan kekuatan F:

Boleh melayani anda: Baki termodinamik: Kelas dan aplikasi

τ = r × F

Menjadi vektor, adalah perlu untuk menyatakan tork yang memberikan magnitud, arah dan makna. Besarnya diberikan oleh:

τ = rf.sin θ

Peraturan yang tepat untuk produk vektor

Apabila masalahnya ada di dalam kapal terbang, alamat tork berserenjang dengan kertas atau skrin dan arah ditentukan oleh peraturan tangan kanan, di mana indeks menunjuk ke arah r, Jari tengah ke arah F dan isyarat ibu jari masuk atau keluar dari kertas.

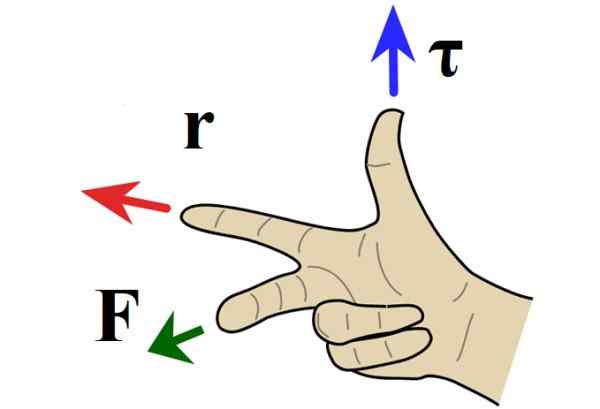Rajah 4. Peraturan tangan kanan untuk produk vektor. Sumber: Wikimedia Commons.

Apabila tork menunjukkan keluar dari kertas, putaran berada di arah yang bertentangan dengan jarum jam dan diberikan tanda positif oleh konvensyen. Jika sebaliknya tork diarahkan ke dalam lembaran, putarannya berada di arah tangan dan tanda negatif.

Untuk mencari tork bersih, titik mudah untuk pengiraan dipilih, yang boleh menjadi yang mana jumlah kuasa terbesar bertindak. Dalam kes ini, momen kuasa ini tidak sah, kerana mempunyai vektor kedudukan r magnitud 0.

Anda boleh memilih mana -mana titik yang menawarkan maklumat yang mencukupi untuk membersihkan yang tidak diketahui yang meminta masalah diselesaikan. Mari lihat dengan lebih terperinci ketika itu.

Latihan diselesaikan

Reflektor angka berikut mempunyai 20 kg jisim dan disokong oleh bar nipis mendatar, jisim dan panjang yang hina, yang dinyatakan pada jawatan. Kabel, juga cahaya, yang membantu mengekalkan reflektor membentuk sudut θ = 30 º dengan bar. Kira:

a) ketegangan dalam kabel

b) Besarnya daya F yang pos di bar melalui engsel.

Penyelesaian

Kami akan menggunakan keadaan keseimbangan pertama Σ F = 0 kepada kuasa yang ditunjukkan dalam rajah:

Boleh melayani anda: haba yang diserap: formula, bagaimana mengira dan diselesaikan latihan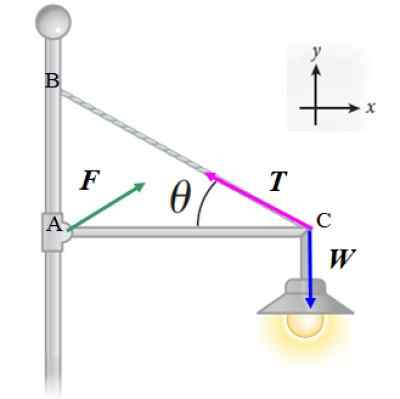

F + T + W = 0

Perhatikan bahawa magnitud dan arah F Mereka belum ditentukan, tetapi kami mengandaikan bahawa ia mempunyai dua komponen: f_x dan f_dan. Dengan cara ini kita mendapat dua persamaan:

F_x -T. cos θ = 0

F_dan - W + t ⋅ sin θ = 0

Sekarang mari kita gunakan keadaan keseimbangan kedua, memilih titik A, kerana kita tidak tahu magnitud F ataupun dari T. Semasa memilih perkara ini, vektor r_Ke tidak sah, oleh itu saatnya F tidak sah dan besarnya F Ia tidak akan muncul dalam persamaan:

-W⋅L + T ⋅Sen θ ⋅ l = 0

Oleh itu:

T.sin θ.L = w.L

T = w/sen θ = (20 kg x 9.8 m/s²) / Dosa 30 º = 392 n

Mengetahui magnitud t kita dapat membersihkan komponen f_x:

F_x = T ⋅ cos θ = 392 cos 30º N = 339. 5 n

Dan kemudian komponen f_dan:

F_dan = W - T ⋅ sin θ = (20 kg x 9.8 m/s²) - 392sss 30 º = 0

Kemudian kita dapat menyatakan F Jadi:

F = 339.5 n x

Oleh itu, daya mendatar. Ini kerana kita menganggap bahawa bar mempunyai berat badan yang hina.

Sekiranya titik C telah dipilih untuk mengira momen yang terhasil, vektor r_T dan r_W Oleh itu, mereka tidak sah:

M = f_{Y ⋅}L = 0

Disimpulkan bahawa f_dan = 0. Oleh itu:

- W + t ⋅ sin θ = 0

T = w/ sin θ

Yang merupakan hasil yang sama pada mulanya diperoleh dengan memilih titik A sebagai tapak di mana paksi putaran berlalu.

Tema minat

Keadaan keseimbangan.

Keadaan keseimbangan pertama.

Rujukan

1. Bedford, 2000. Ke. Mekanik untuk Kejuruteraan: Statik. Addison Wesley.
2. Figueroa, d. (2005). Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 4. Sistem zarah. Diedit oleh Douglas Figueroa (USB).
3. Giancoli, d.  2006. Fizik: Prinsip dengan aplikasi. 6th. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Fizik universiti dengan fizik moden. Ke -14. Ed. Jilid 1.
5. Serway, r., Jewett, J. (2008). Fizik untuk Sains dan Kejuruteraan. Jilid 1. Ke -7. Ed. Pembelajaran Cengage.