Sudut bertentangan dengan puncak (dengan senaman yang diselesaikan)

The Sudut bertentangan dengan puncak Mereka adalah orang -orang yang memenuhi perkara berikut: sisi salah satu daripadanya adalah pemanjangan sisi sudut yang lain. Dia Teorem Asas Sudut bertentangan dengan puncaknya dikatakan: dua sudut yang ditentang oleh puncak mempunyai ukuran yang sama.

Banyak kali bahasa disalahgunakan dengan mengatakan bahawa sudut yang ditentang oleh puncak adalah sama, yang tidak betul. Hakikat bahawa dua sudut mempunyai ukuran yang sama tidak bermaksud bahawa mereka sama. Seperti mengatakan bahawa dua anak yang mempunyai ketinggian yang sama adalah sama.

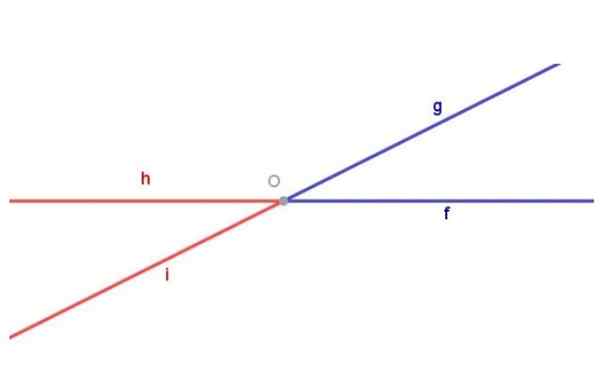
Rajah 1. Sudut bertentangan dengan puncak. Disediakan oleh: Fanny Zapata.

Ingatlah bahawa sudut ditakrifkan sebagai angka geometri yang terdiri daripada dua separuh -pentasan dengan asal yang sama.

Rajah 1 menunjukkan sudut Kabut (Biru) terdiri daripada separuh -rekreasi [OF) Dan separuh pertarungan [OG) asal biasa Sama ada. Rajah 1 juga menunjukkan sudut Hoi (merah) terdiri daripada separuh -rekreasi [Saya dengar) Dan separuh pertarungan [Oh) kedua -duanya dengan asal Sama ada. 

Dua sudut bertentangan dengan puncak adalah dua angka geometri yang berbeza. Untuk menyerlahkan ini, dalam Rajah 1 sudut telah berwarna Kabut Biru, sementara sudut Hoi Dia berwarna merah. 

Sudut biru dan merah Rajah 1 ditentang oleh puncak kerana: separuh [OF) sudut biru adalah pemanjangan separuh [Oh) sudut merah dan separuh [OG) sudut biru adalah pemanjangan separuh [Saya dengar) sudut merah.

[TOC]

Konsep penting mengenai sudut

Sisi dan simpang sudut

Angka geometri yang terdiri daripada dua separuh masa dengan asal biasa adalah sudut. Imej berikut menunjukkan sudut Poq dibentuk oleh dua separuh [OP) dan [OQ) asal biasa Sama ada:

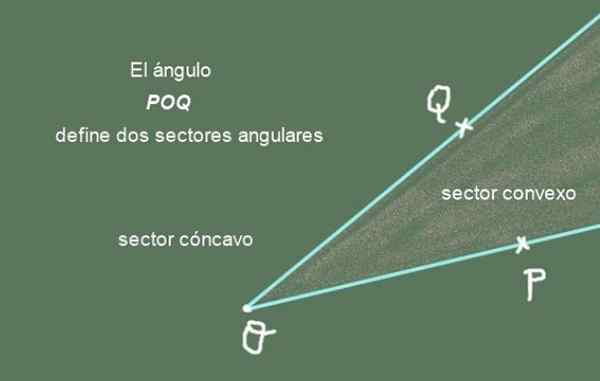Rajah 2. Sudut POQ mentakrifkan dua sektor sudut. Disediakan oleh: f. Zapata.

Semi -straight [OP) dan [OQ) adalah sisi sudut Poq, sementara titik umum atau dipanggil Vértice sudut.

Boleh melayani anda: Sturges memerintah

Sektor sudut: Sudut membahagikan satah yang mengandunginya menjadi dua sektor sudut. Salah satunya adalah sektor sudut cembung dan yang lain adalah sektor sudut cekung. Kesatuan kedua -dua sektor memberikan pesawat penuh.

Rajah 2 menunjukkan pada sudut Poq dan dua sektor sudutnya. Sektor sudut cembung adalah yang mempunyai bentuk yang tajam, sementara cekung adalah sektor sudut pesawat yang hilang sektor cembung.

Sudut yang dibentuk oleh dua baris yang dipotong

Dua baris satah yang dipintas bentuk empat sudut dan membahagikan satah menjadi empat sektor sudut.

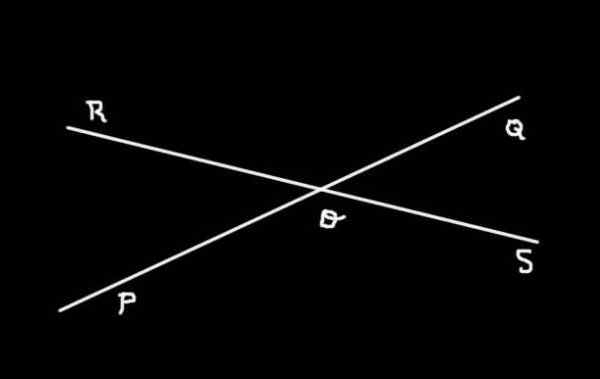Rajah 3. Garis (PQ) dan (Rs) dipintas dalam O dan Borang 4 Sudut. Disediakan oleh: f. Zapata.

Rajah 3 menunjukkan dua baris (PQ) dan (Rs) dipintas dalam Sama ada. Di sana anda dapat melihat bahawa empat sudut ditentukan:

-Soq, Qor, Rop dan Pos

Sudut Soq dan Qor, Qor dan ROP, ROP dan Pos, Pos dan Soq adalah  sudut bersebelahan antara mereka, sementara Soq dan Rop Mereka ditentang oleh puncak. Mereka juga Sudut bertentangan dengan puncak Sudut Qor dan Pos.

Garis tegak lurus dan sudut lurus

Dua garisan pengeringan (garis lurus bersilang) adalah Garis lurus tegak lurus Sekiranya mereka menentukan empat sektor sudut yang sama. Sekiranya setiap empat sektor bersimetris dengan sektor sudut bersebelahan, maka mereka mempunyai ukuran yang sama.

Setiap sudut yang menentukan dua garis tegak lurus dipanggil sudut kanan. Semua sudut lurus mempunyai ukuran yang sama.

Separa -straight pada garis yang sama dan sudut rata

Memandangkan garis dan titik itu, dua separuh persegi ditakrifkan. Kedua -dua setengahnya menentukan dua Sudut rata.

Dalam Rajah 3 baris dapat diperhatikan (Rs) dan titik Sama ada yang dimiliki (Rs). Sudut Sor Ia adalah sudut rata. Ia juga boleh disahkan bahawa sudut ROS Ia adalah sudut rata. Semua sudut rata mempunyai ukuran yang sama.

Boleh melayani anda: harta benda clausurative

Sudut null dan sudut penuh

Satu separuh rekreasi mentakrifkan dua sudut: salah satu daripada mereka dalam sektor sudut cembung adalah sudut null Dan yang lain, sektor sudut cekung adalah sudut penuh. Dalam Rajah 3 sudut null Sos dan juga sudut penuh Sos. 

Pengukuran 

Terdapat dua sistem berangka yang sering digunakan untuk memberikan pengukuran sudut. 

Salah satu daripada mereka adalah sistem sexagesimal, iaitu, berdasarkan nombor 60. Ini adalah warisan budaya Mesopotamia kuno. Sistem pengukuran sudut lain adalah sistem radián, berdasarkan nombor π (pi) dan merupakan warisan orang bijak kuno yang mengembangkan geometri.

Sistem Sexagesimal

Sudut Null: Dalam sistem sexagesimal, sudut null berukuran 0º (sifar darjah).

Sudut Penuh: Langkah 360º diberikan (tiga ratus enam puluh darjah).

Sudut rata: Dalam sistem sexagesimal, sudut rata berukuran 180º (seratus delapan puluh darjah).

Sudut Kanan: Dua garis tegak lurus membahagikan satah menjadi empat sudut ukuran yang sama yang disebut sudut lurus. Ukuran sudut kanan adalah seperempat sudut penuh, iaitu 90º (sembilan puluh darjah).

Penghantar atau goniometer

Penghantar adalah instrumen yang digunakan untuk mengukur sudut. Ia terdiri daripada separuh bulatan (biasanya plastik telus) dibahagikan kepada 180 bahagian sudut. Sebagai separuh bulatan membentuk sudut rata, maka ukuran antara dua bahagian berturut -turut adalah 1.

Goniometer serupa dengan pengangkut dan terdiri daripada bulatan yang dibahagikan kepada 360 bahagian sudut.

Sudut yang sisinya bermula dari pusat goniometer memintas dua sektor dan ukuran sudut dalam darjah adalah sama dengan bilangan n bahagian antara kedua -dua sektor yang dicegat, dalam hal ini ukurannya akan menjadi No (berbunyi ""Ene darjah").

Ia boleh melayani anda: sentimeter persegi hingga meter persegi (cm² hingga m²)

Teorem sudut bertentangan dengan puncak

Secara rasmi, teorem dinyatakan dengan cara ini:

Sekiranya dua sudut menentang puncak, maka mereka mempunyai ukuran yang sama.

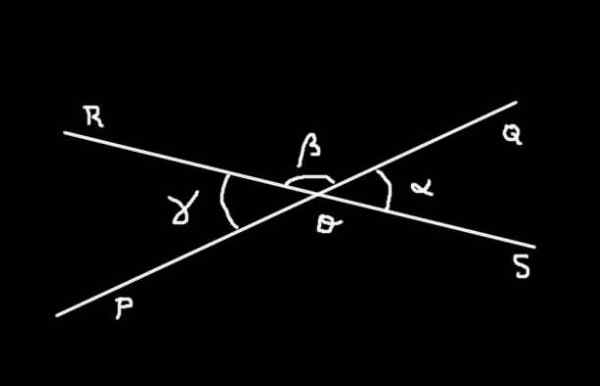Rajah 4. α, β dan γ adalah ukuran sudut SOQ, QOR dan ROP. Disediakan oleh: f. Zapata.

Demonstrasi

Sudut Soq Ia mempunyai ukuran α; sudut Qor Ia mempunyai ukuran β dan sudut Rop Ia mempunyai ukuran γ. Jumlah sudut Soq lebih banyak dia Qor membentuk sudut rata Sor ukuran 180º.

Itu dia:

α + β = 180º

Sebaliknya dan menggunakan alasan yang sama dengan sudut Qor dan Rop Kamu ada:

β + γ = 180º

Sekiranya kita melihat dua persamaan sebelumnya, satu -satunya cara yang dipenuhi adalah bahawa α adalah sama dengan γ.

Sebagai Soq Ia mempunyai ukuran α dan ditentang oleh puncak ke Rop ukuran γ, dan sebagai α = γ, disimpulkan bahawa sudut yang ditentang oleh puncak mempunyai ukuran yang sama.

Latihan diselesaikan

Merujuk kepada Rajah 4: Anggapkan bahawa β = 2 α. Cari ukuran sudut Soq, Qor dan Rop Dalam tahap seksis.

Penyelesaian

Seperti jumlah sudut Soq lebih banyak dia Qor membentuk sudut rata Sor Kamu ada:

α + β = 180º

Tetapi mereka memberitahu kita bahawa β = 2 α. Menggantikan nilai β ini kita kekal:

α + 2 α = 180º

Iaitu:

3 α = 180º

Yang bermaksud bahawa α adalah bahagian ketiga 180º:

α = (180º / 3) = 60º

Kemudian ukuran Soq adalah α = 60º. Ukuran Qor IS β = 2 α = 2*60º = 120º. Akhirnya sebagai Rop ditentang oleh puncak ke Soq Kemudian mengikut teorem sudah menunjukkan mereka mempunyai ukuran yang sama. Iaitu ukuran Rop adalah γ = α = 60º. 

Rujukan

1. Baldor, j. Ke. 1973.Geometri rata dan ruang. Kebudayaan Amerika Tengah. 
2. Undang -undang dan formula matematik. Sistem pengukuran sudut. Diperolehi dari: Ingemecanica.com.
3. Wikipedia. Sudut bertentangan dengan puncak. Pulih dari: Adakah.Wikipedia.com
4. Wikipedia. Penghantar. Pulih dari: Adakah.Wikipedia.com
5. Zapata f. Goniometer: Sejarah, Bahagian, Operasi. Diperolehi dari: Lifer.com