Matematik

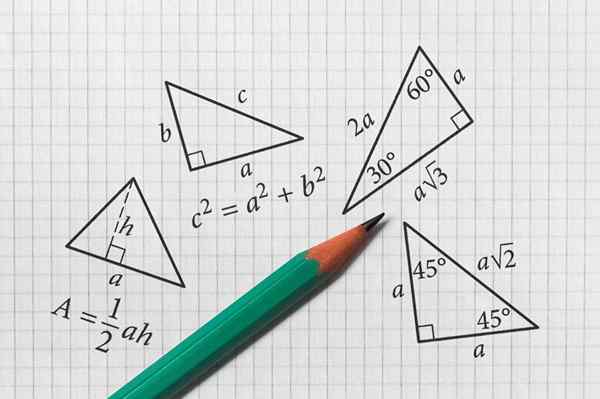
Sudut dan segitiga

Sudut dan segitiga
Sudut dan segitiga adalah sebahagian daripada geometri rata. Shuttersock

Apakah sudut dan segitiga?

A sudut Ia adalah kawasan pesawat yang dibatasi oleh dua separuh persamaan dengan titik asal yang sama. Perkara ini dikenali sebagai puncak, sementara separuh -persegi dipanggil sisi. Sebaliknya, a Segitiga Ia adalah angka tiga sudut dan tiga sisi, dengan tiga simpang.

Kami akan bercakap mengenai sudut terlebih dahulu.

Sudut

Terdapat beberapa cara untuk menunjukkan sudut: melalui huruf Yunani seperti α, β, γ, yang mana aksen circumflex boleh ditambah; dengan huruf besar berlapis atau huruf kecil, A, B, C, A, B, C; nombor, seperti 1, 2, 3 ... atau menggunakan simbol sudut ∠.

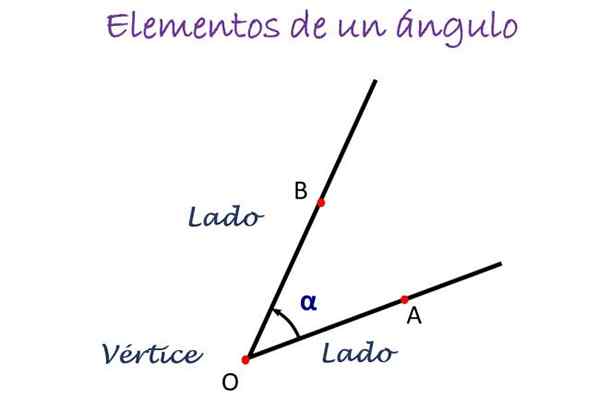Unsur utama sudut. Sumber: f. Zapata

Dalam angka di atas, sudut diukur dari sisi a ke b, ditunjukkan oleh arah anak panah, dan di tengah huruf yang menandakan puncak diletakkan, yang biasanya atau. Sudut kemudian dilambangkan sebagai ∠ AOB.

Apabila sudut diukur dalam pengertian antihorarium, tanda +ditugaskan sewenang -wenangnya, dan jika ia diukur dalam jadual, tanda -untuk membezakannya.

Ukuran sudut dilakukan dengan cara pengangkut, yang terdiri daripada lembaran plastik separuh bulatan seperti yang ditunjukkan di bawah. Separuh bulatan dibahagikan kepada 180 bahagian yang sama, setiap panggilan ijazah.

Untuk mengukur, puncak sudut bertepatan dengan titik pusat pengangkut, ditunjukkan dengan anak panah, dan bahagian awal dengan salah satu tepi, dalaman atau luaran. Bahagian akhir merentasi beberapa tanda pengangkut, langkah ini menjadi sudut.

Boleh melayani anda: Peraturan empirikal: Cara Memohonnya, Apa Latihan Latihan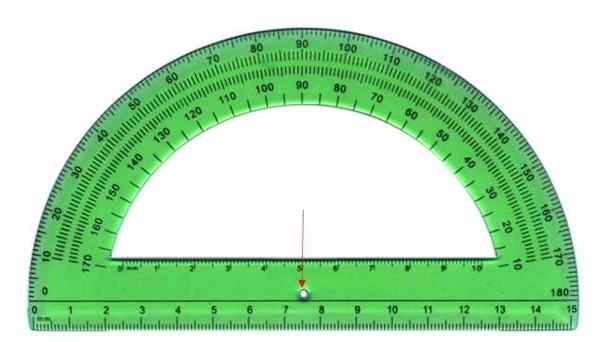Penghantar adalah instrumen untuk mengukur sudut. Sumber: Wikimedia Commons

Jenis sudut

Salah satu kriteria yang paling banyak digunakan untuk mengklasifikasikan sudut, adalah mengikut ukurannya. Oleh itu, sudut boleh:

  • Batal, Langkah 0º.
  • Tajam, ukurannya adalah antara 0 dan 90º.
  • Lurus, Ia mengukur tepat 90º.
  • Bodoh, Lebih besar daripada 90º dan kurang daripada 180º.
  • Rata, Ukurannya sama dengan 180º.
  • Lengkap, mewakili giliran lengkap dan mengukur 360º.
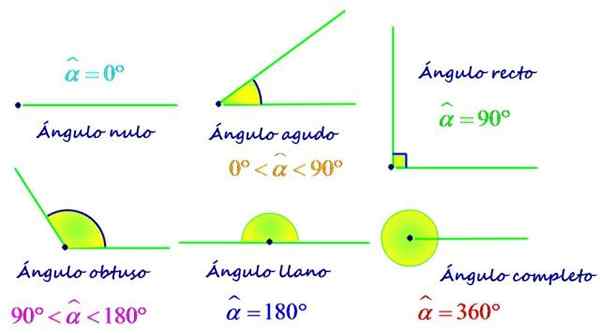Jenis sudut mengikut ukuran anda. Sumber: f. Zapata.

Mengikut hubungan antara ukurannya dan sudut rata, iaitu 180º, sudut juga boleh diklasifikasikan sebagai:

  • Cekung, Sekiranya ia berukuran kurang daripada 180º. Oleh itu, sudut akut, lurus dan bodoh adalah cekung, kerana ukurannya selalu kurang dari 180º (lihat angka di atas).
  • Cembung, Sekiranya ukuran anda lebih besar daripada 180º, kerana sudut 270º dan 360º.

Sudut mengikut jumlah langkah mereka dan mengikut kedudukan mereka

Dua sudut ∠ A dan ∠ B boleh:

  • Pelengkap, Sekiranya jumlah langkahnya sama dengan 90º.
  • Tambahan, Apabila menambah langkah masing -masing, 180º diperolehi.
  • Konjugasi, Sekiranya jumlah ini sama dengan 360º.
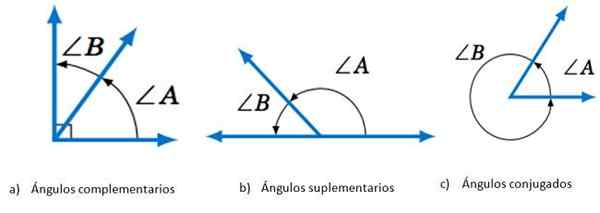Sudut mengikut jumlah langkahnya. Sumber: Matematik Librettexts.

Bagi kedudukan sisi mereka, dua sudut boleh:

  • Dalam barisan, Ketika puncak dan salah satu sisi mempunyai persamaan.
  • Bersebelahan, Sekiranya mereka berturut -turut, tetapi pihak yang tidak biasa bertentangan, jadi mereka juga tambahan.
  • Bertentangan dengan puncak, Apabila mereka mempunyai puncak biasa, dan sisi sudut berpanjangan ke arah yang bertentangan.
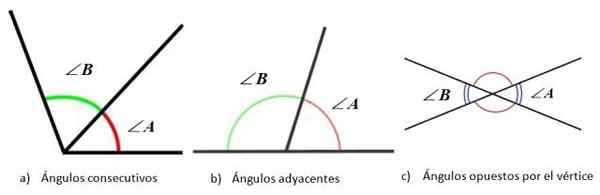Sudut mengikut kedudukan relatif di antara sisinya. Sumber: f. Zapata

Segitiga

Segitiga adalah tokoh geometri yang rata dan tertutup, milik keluarga poligon, dengan tiga sisi terdiri daripada garis yang dipotong dua hingga dua, menghasilkan tiga sudut.

Ia dapat melayani anda: fungsi bijjective: apa itu, bagaimana ia dilakukan, contoh, latihan

Unsur -unsur asasnya adalah:

  • Simpang, yang merupakan titik persimpangan garis yang disebutkan di atas.
  • Sisi, sejumlah 3 dan yang terdiri daripada segmen garisan yang menyambung ke simpang.
  • Sudut dalaman, Juga dalam jumlah 3, jumlahnya selalu sama dengan 180º.

Umumnya, sisi dilambangkan dengan huruf kecil Latin, simpul dengan huruf besar dan sudut dengan huruf kecil yang kecil, tetapi notasi lain juga mungkin.

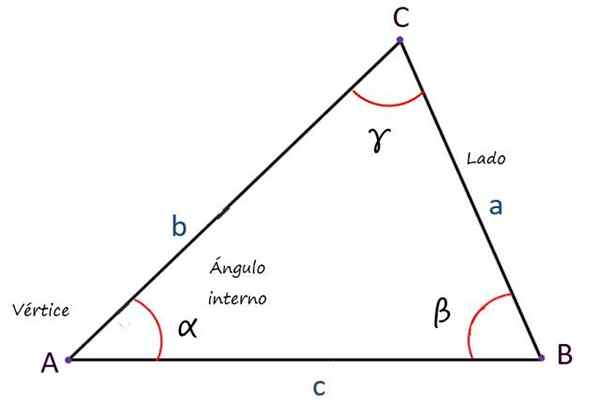Unsur utama segitiga. Sumber: f. Zapata

Jenis segitiga

Segitiga mengikut bentuk sisinya

Mengikut kriteria ini, segitiga boleh:

  • Keseimbangan, Sekiranya tiga pihaknya mempunyai ukuran yang sama.
  • Isosceles, Apabila hanya dua sisi mempunyai ukuran yang sama, sementara yang ketiga berbeza.
  • Scalene, Sekiranya ketiga -tiga sisi adalah saiz yang berbeza.
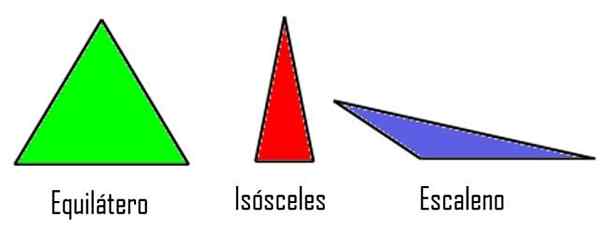Segitiga mengikut sisi mereka. Modified Wikimedia Commons

Segitiga mengikut sudut dalamannya

Kriteria ini berdasarkan jenis sudut dalaman segitiga. Menurut ini, segitiga boleh:

  • Acutangle, Apabila tiga sudut dalaman segitiga itu akut.
  • Rectangle, Sekiranya segitiga mempunyai sudut ukuran dalaman yang sama dengan 90º.
  • Bodoh, Salah satu sudut dalaman segitiga adalah bodoh.
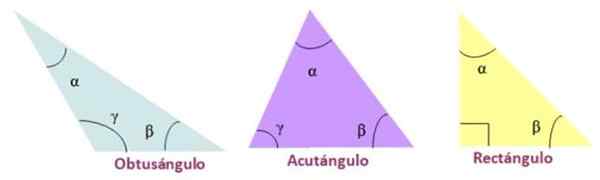Jenis segitiga mengikut sudut dalamannya. Sumber: f. Zapata

Segmen segitiga yang terkenal

Antara segmen yang terkenal di mana -mana segitiga, mereka mempunyai:

  • Median, segmen yang diarahkan dari puncak, terus ke seberang.
  • MEDIRIX, Ia adalah segmen milik garis tegak lurus ke sisi, yang bersilang ke titik tengah di sebelah itu.
  • Bisector, segmen yang membahagikan sudut dalaman menjadi dua bahagian yang sama, dan yang meluas ke seberang ke sudut.
  • Ketinggian, segmen tegak lurus ke sisi, yang meluas ke puncak yang bertentangan.
Boleh melayani anda: Interpolasi LaGrange

Tiga medium, tiga meditrices dapat dikesan dan sebagainya.

Pusat Segitiga

Di mana -mana segitiga, perkara berikut menonjol (lihat angka berikut):

  • Baricentro g, juga kadang -kadang dipanggil Centroid segitiga, ia adalah titik persimpangan median dan sentiasa pedalaman ke segitiga.
  • Ortocenter h, titik di mana tiga ketinggian bersilang.
  • Circumcentro atau, Ia adalah titik persimpangan meditrices. Ia boleh didapati di luar segitiga, jika ini bodoh, manakala, di segitiga segi empat tepat, atau bertepatan dengan titik tengah hipotenus.
  • Insenter, Titik persimpangan untuk bisector segi tiga.
  • Euler lurus, lurus yang menyatukan balicenter, orthocenter dan circumcentro, di mana -mana segitiga yang tidak sama rata. Selalu dipenuhi bahawa panjang segmen Hg adalah dua kali ganda dari segmen Go.
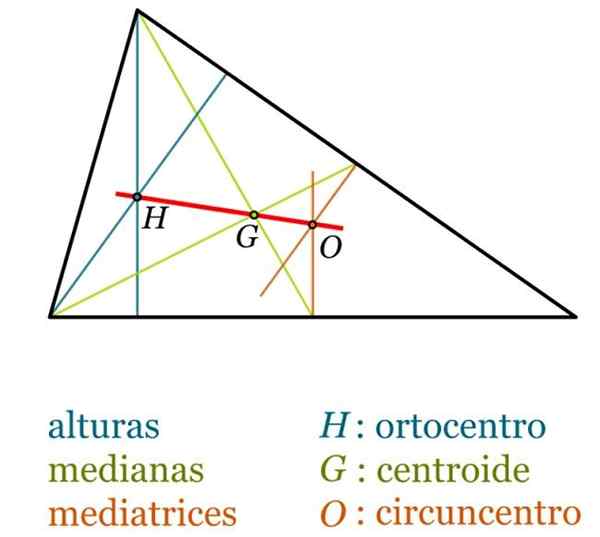Mata dan segmen segitiga yang ketara. Sumber: Wikimedia Commons

Kawasan segitiga

Untuk mengira kawasan A segitiga, formula berikut digunakan, sifat umum:

A = asas × ketinggian / 2

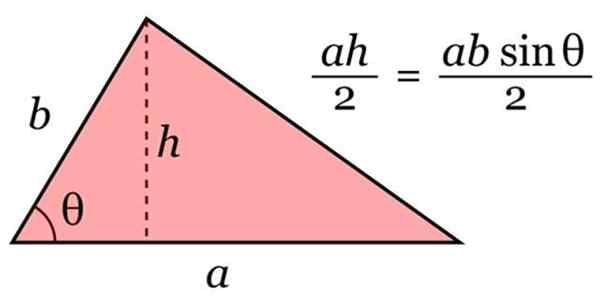Kawasan segitiga. Sumber: Wikimedia Commons

Formula Herón

Mengetahui panjang semua sisi segitiga, formula berikut, yang dikenali sebagai Formula Herón, Membolehkan anda mencari kawasan A:

Di sini, sisi segitiga adalah A, B dan C, sementara sp Adakah dia Semi -perimeter, iaitu separuh perimeter p = a + b + c.

Rujukan

  1. Alexander, d. 2013. Geometri. 5th. Edisi. Pembelajaran Cengage.
  2. Sudut. Matematik Librettx. Pulih dari: matematik.Libretxts.org.
  3. Jiménez, René. 2010. Matematik II (Geometri dan Trigonometri). 2. Edisi. Pearson.
  4. Formula Universe. Segitiga. Pulih dari: universoformulas.com.
  5. Zapata, f. Segitiga: Sejarah, Unsur, Klasifikasi, Hartanah. Diperolehi dari: Lifer.com.