Nombor atau nombor euler e berapa bernilai, hartanah, aplikasi

Dia Nombor atau nombor euler e Ia adalah pemalar matematik yang terkenal yang sering muncul dalam pelbagai aplikasi saintifik dan ekonomi, bersama -sama dengan nombor π dan nombor penting lain dalam matematik.

Kalkulator saintifik melemparkan nilai berikut untuk nombor e:

Rajah 1. Nombor Euler sering muncul dalam sains. Sumber: f. Zapata.

E = 2.718281828 ..

Tetapi banyak lagi perpuluhan yang diketahui, sebagai contoh:

E = 2.71828182845904523536 ..

Dan komputer moden telah membenarkan trilion perpuluhan ke nombor e.

Ia adalah nombor tidak rasional, yang bermaksud bahawa ia mempunyai jumlah perpuluhan yang tidak terhingga tanpa corak berulang (urutan 1828 muncul dua kali pada awal dan tidak lagi mengulangi).

Dan ini juga bermaksud bahawa nombor e tidak dapat diperolehi sebagai quotient dari dua nombor keseluruhan.

[TOC]

Sejarah

Jumlah dan Dia dikenal pasti oleh saintis Jacques Bernoulli pada tahun 1683 ketika dia mempelajari masalah kepentingan kompaun, tetapi sebelum ini dia secara tidak langsung muncul dalam karya -karya matematik Scotland John Napier, yang mencipta logaritma untuk 1618.

Walau bagaimanapun, ia adalah Leonhard Euler pada tahun 1727 yang memberinya nama nombor E dan secara intensif mempelajari sifatnya. Itulah sebabnya ia juga dikenali sebagai Nombor Euler dan juga sebagai asas semula jadi untuk logaritma neperian (eksponen) yang digunakan.

Berapa nombor e yang bernilai?

Nombor e vale:

E = 2.71828182845904523536 ..

Titik yang menggalakkan bermaksud bahawa terdapat jumlah perpuluhan yang tidak terhingga dan sebenarnya, berjuta -juta daripadanya dikenali dengan komputer semasa.

Perwakilan nombor e

Terdapat beberapa cara untuk menentukan e yang kita terangkan di bawah:

Nombor E sebagai had

Salah satu daripada pelbagai cara di mana nombor E dinyatakan adalah yang ditemui oleh saintis Bernoulli dalam karyanya atas kepentingan kompaun:

Di mana anda mesti melakukan nilai n jumlah yang sangat besar.

Sangat mudah untuk diperiksa, dengan bantuan kalkulator, ketika itu n Sangat besar, ungkapan sebelumnya cenderung kepada nilai dan diberikan di atas.

Ia dapat melayani anda: fungsi bijjective: apa itu, bagaimana ia dilakukan, contoh, latihan

Sudah tentu kita dapat bertanya kepada diri sendiri betapa besarnya ia dapat dilakukan n, Oleh itu, kita cuba dengan nombor bulat, seperti ini:

n = 1000; 10.000 atau 100.000

Dalam kes pertama anda mendapat E = 2.7169239 .. . Pada kedua e = 2.7181459 ... dan pada ketiga ia lebih dekat dengan nilai dan: 2.7182682. Kita sudah dapat muncul dengan n = 1.000.000 atau lebih besar, pendekatan akan lebih baik.

Dalam bahasa matematik, prosedur membuat n Ia semakin dekat dan lebih banyak nilai yang sangat besar, ia dipanggil Had ke Infinity Dan ia dilambangkan seperti ini:

Untuk menunjukkan tak terhingga, simbol "∞" digunakan.

Nombor e sebagai jumlah

Ia juga mungkin untuk menentukan nombor E melalui operasi ini:

Angka -angka yang muncul dalam penyebut: 1, 2, 6, 24, 120 ... sesuai dengan operasi n!, Di mana:

n! = n. (N-1).(N-2). (N-3) ..

Dan dengan definisi 0! = 1.

Sangat mudah untuk mengesahkan bahawa penambahan lebih banyak ditambah, semakin besar bilangannya dicapai dan.

Mari buat beberapa ujian dengan kalkulator, menambah penambahan:

1 +1+ (1/2) + (1/6) = 2.71667

1 +1+ (1/2) + (1/6) + (1/24) = 2.75833

1 +1+ (1/2) + (1/6) + (1/24) + (1/120) = 2.76667

1 +1+ (1/2) + (1/6) + (1/24) + (1/120) + (1/720) = 2.71806

Semakin banyak istilah yang ditambah kepada jumlahnya, semakin banyak hasilnya sama dengan dan.

Ahli matematik membuat notasi padat untuk jumlah ini yang melibatkan banyak istilah, menggunakan simbol jumlah σ:

Ungkapan ini dibaca sebagai "jumlah n = 0 hingga infiniti 1 antara n faktorial".

Nombor E dari sudut pandangan geometri

Nombor E mempunyai perwakilan grafik yang berkaitan dengan kawasan di bawah graf lengkung:

y = 1/x

Apabila nilai x adalah antara 1 dan E, kawasan ini bernilai 1, seperti yang digambarkan dalam angka berikut:

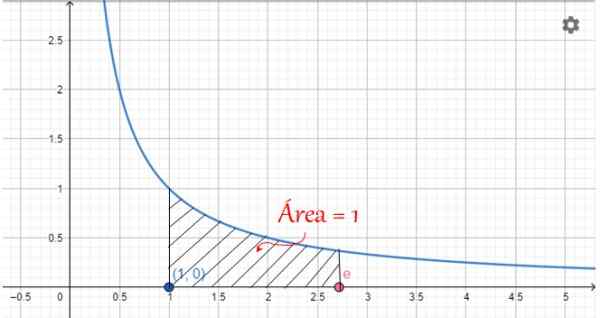Rajah 2. Perwakilan grafik Nombor E: Kawasan di bawah lengkung 1/x, antara x = 1 dan x = e o'clock. Sumber: f. Zapata.

Nombor E Properties

Beberapa sifat nombor E adalah:

Boleh melayani anda: Fungsi Berkembang: Cara Mengenalpasti, Contoh, Latihan

-Ia tidak rasional, dengan kata lain, ia tidak dapat diperoleh hanya dengan membahagikan dua nombor keseluruhan.

-Jumlah dan Ia juga a Nombor transenden, yang bermaksud dan Ia bukan penyelesaian persamaan polinomial.

-Ia berkaitan dengan empat nombor terkenal lain dalam bidang matematik, iaitu: π, i, 1 dan 0, melalui identiti Euler:

dan^πi + 1 = 0

-Panggilan nombor kompleks boleh dinyatakan melalui e.

-Ia merupakan asas logaritma semulajadi atau neperian hari ini (definisi asal John Napier sedikit berbeza).

-Ia adalah satu -satunya nombor seperti logaritma Neperiannya bernilai 1, iaitu:

 ln e = 1

Aplikasi

Statistik

Nombor E kelihatan sangat kerap dalam bidang kebarangkalian dan statistik, yang terdapat dalam pelbagai pengedaran, seperti normal atau Gaussian, Poisson dan lain -lain.

Kejuruteraan

Dalam kejuruteraan, ia adalah kerap, kerana fungsi eksponen y = e^x Ia hadir dalam mekanik dan elektromagnetisme, sebagai contoh. Antara banyak aplikasi yang boleh kami kutip:

-Kabel atau rantai yang tergantung pada hujungnya, mengamalkan bentuk lengkung yang diberikan oleh:

y = (e^x + dan^-x) /2

-A Condenser C pada mulanya dilepaskan, yang menghubungkan secara siri kepada rintangan r dan sumber voltan V untuk memuatkan, memperoleh beban tertentu q bergantung pada masa yang diberikan oleh:

Q (t) = cv (1-e^-T/rc)

Biologi

Fungsi eksponen y = a.dan^Bx, Dengan malar A dan B, ia digunakan untuk memodelkan pertumbuhan sel dan pertumbuhan bakteria.

Fizikal

Dalam fizik nuklear, kerosakan radioaktif dan penentuan umur dimodelkan oleh radiokarbon bertarikh.

Ekonomi

Dalam pengiraan kepentingan komposit, bilangan E timbul secara semula jadi.

Katakan anda mempunyai sejumlah wang P_{Sama ada}, untuk melabur pada kadar faedah tahunan.

Sekiranya wang itu ditinggalkan selama 1 tahun, selepas masa itu anda akan mempunyai:

P (1 tahun) = P_{Sama ada} + P_{Sama ada}.i = p_{Sama ada} (1+ i)

Selepas setahun lagi tanpa menyentuhnya, anda akan mempunyai:

Boleh melayani anda: kebarangkalian teoritis: bagaimana untuk mengeluarkannya, contoh, latihan

P (2 tahun) = P_{Sama ada} + P_{Sama ada}.i + (p_{Sama ada} + P_{Sama ada} .i) i = p_{Sama ada} +2 p_{Sama ada}.i + p_{Sama ada}.Yo²  = Po (1+i)²

Dan dengan cara ini oleh n tahun:

P = p_{Sama ada} (1+i)ⁿ

Sekarang ingat salah satu definisi E:

Ia kelihatan seperti ungkapan untuk p, jadi mesti ada hubungan.

Kami akan mengedarkan kadar faedah nominal Yo dalam n Tempoh masa, dengan cara ini kadar faedah kompaun akan menjadi i/n:

P = p_{Sama ada} [1+ (i/n)]ⁿ

Ungkapan ini kelihatan sedikit lebih banyak mengenai had kami, tetapi belum sama.

Walau bagaimanapun, selepas beberapa manipulasi algebra, dapat ditunjukkan bahawa membuat perubahan pembolehubah ini:

h = n/i → i = n/h

Wang kita p menjadi:

P = p_{Sama ada} [1+ (1/h)]^Hai = P_{Sama ada} [1+ (1/h)]^hYo

Dan apa yang ada di antara kunci, walaupun ia ditulis dengan surat itu h, Ia sama dengan hujah had yang mentakrifkan nombor E, hilang hanya mengambil had.

Mari lakukan  h → ∞, dan apa yang ada di antara kunci berubah menjadi nombor dan. Ini tidak bermaksud bahawa kita perlu menunggu masa yang besar untuk mengeluarkan wang kita.

Sekiranya kita kelihatan baik, semasa melakukan H = n/i Dan cenderung kepada ∞, apa yang telah kami lakukan adalah untuk mengedarkan kadar faedah dalam tempoh masa yang sangat kecil: sangat kecil:

I = n/h

Ini dipanggil Permodalan berterusan. Dalam kes ini, jumlah wang mudah dikira seperti berikut:

P = p_{Sama ada} .dan^Yo

Di mana saya adalah kadar faedah tahunan. Sebagai contoh, dengan mendepositkan € 12 hingga 9 % setahun, melalui permodalan berterusan, selepas satu tahun anda mempunyai:

P = 12 x e^{0.09 × 1} € = 13.€ 13

Dengan keuntungan 1.13 €.

Rujukan

1. Nikmati matematik. Kepentingan Kompaun: Komposisi Berkala. Pulih dari: nikmatMatimaticas.com.
2. Figuera, j. 2000. Matematik 1st. Dipelbagaikan. Edisi bersama.
3. Garcia, m. Nombor e dalam pengiraan asas. Pulih dari: matematik.Ciens.UCV.Pergi.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Larson, r. 2010. Pengiraan pemboleh ubah. 9NA. Edisi. McGraw Hill.