Sifat nombor khayalan, aplikasi, contoh

The Nombor khayalan Mereka adalah mereka yang memberikan penyelesaian kepada persamaan di mana yang tidak diketahui, persegi tinggi, sama dengan nombor negatif sebenar. Unit khayalan adalah I = √ (-1).

Dalam persamaan: z²= - a, z Ia adalah nombor khayalan yang dinyatakan seperti berikut:

 Z = √ (-a) = i√ (a)

Menjadi ke Nombor sebenar positif. Yeah A = 1, Jadi z = i, di mana Yo adalah unit khayalan.

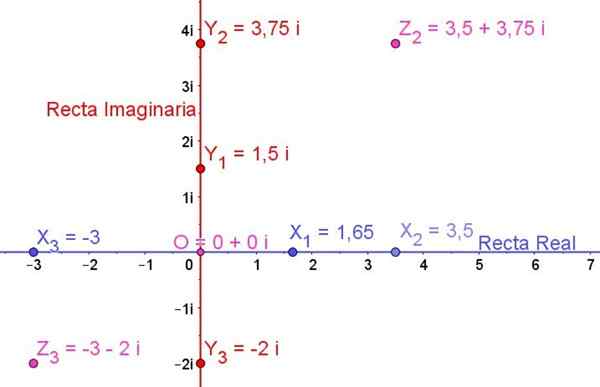Rajah 1. Satah kompleks menunjukkan beberapa nombor sebenar, beberapa nombor khayalan dan beberapa nombor kompleks. Sumber: f. Zapata.

Secara umum, nombor khayalan Z sentiasa dinyatakan dalam bentuk: 

z = y ⋅ i

Di mana dan Ia adalah nombor sebenar dan Yo adalah unit khayalan.

Serta nombor sebenar diwakili pada baris, yang dipanggil Lurus sebenar, Analogi nombor khayalan diwakili di Khayalan lurus.

The Khayalan lurus Selalunya ortogonal (90º bentuk) ke Lurus sebenar dan kedua -dua baris menentukan pesawat Cartesian yang disebut Satah kompleks.

Rajah 1 menunjukkan satah kompleks dan beberapa nombor sebenar, beberapa nombor khayalan dan juga beberapa nombor kompleks yang diwakili di atasnya:

X₁, X₂, X₃ Mereka adalah nombor sebenar

Dan₁, Dan₂, Dan₃ Mereka adalah nombor khayalan

Z₂ dan z₃ Mereka adalah nombor yang kompleks

Nombor atau sifar sebenar dan juga sifar khayalan, sehingga asal atau kompleks sifar yang dinyatakan oleh:

0 + 0i 

[TOC]

Sifat

Set nombor khayalan dilambangkan oleh:

I = ..., -3i, ..., -2i, .. .,-Yo, .. .,0i, .. .,Yo, .. .,2i, .. .,3i, ...

Dan beberapa operasi mengenai set berangka ini boleh ditakrifkan. Nombor khayalan tidak selalu diperoleh dari operasi ini, jadi kami akan melihatnya dengan sedikit lebih terperinci:

Jumlah dan penolakan khayalan

Nombor khayalan boleh menambah dan tolak antara satu sama lain dan hasilnya akan ada nombor khayalan baru. Sebagai contoh:

Boleh melayani anda: sepupu relatif: apa, penjelasan, contoh

 3i + 2i = 5i

4i - 7i = -3i

Produk khayalan

Apabila produk nombor khayalan dengan yang lain dibuat, hasilnya adalah nombor sebenar. Mari kita lakukan operasi berikut untuk memeriksa:

2i x 3i = 6 x i² = 6 x (√ (-1))² = 6 x (-1) = -6.

Dan seperti yang kita lihat, -6 adalah nombor sebenar, walaupun ia telah diperoleh dengan mengalikan dua nombor khayalan tulen.

Produk nombor sebenar untuk khayalan lain

Sekiranya nombor sebenar didarabkan oleh saya, hasilnya akan menjadi nombor khayalan, yang sepadan dengan putaran 90 darjah.

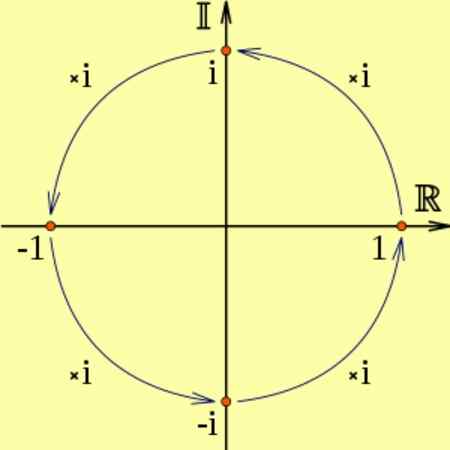
Dan adakah saya² sepadan dengan dua putaran berturut -turut 90 darjah, yang bersamaan dengan mendarab dengan -1, iaitu i² = -1. Ia dapat dilihat dalam rajah berikut:

Rajah 2. Pendaraban oleh unit khayalan dan sepadan dengan putaran 90º. Sumber: Wikimedia Commons.

Sebagai contoh:

-3 x 5i = -15i

-3 x i = -3i.

Potentiasi khayalan

Potentiasi nombor khayalan ke seluruh eksponen dapat ditakrifkan:

Yo¹ = i

Yo² = i x i = √ (-1) x √ (-1) = -1

Yo³ = i x i² = -I

Yo⁴ = i² x i² = -1 x -1 = 1

Yo⁵ = i x i⁴ = i

Secara umum anda mesti Yoⁿ = i^(n mod 4), di mana Mod Ia adalah sisa pembahagian antara n dan 4.

Potensi bilangan bulat negatif juga boleh dibuat:

Yo^-1 = 1 / i¹ = i / (i x i¹) = I / (i²) = I / (-1) = -i

Yo-² = 1 / i² = 1/ (-1) = -1

Yo-³= 1 / i³ = 1 / (-i) = (-1) / i = -1 x i^-1 = (-1) x (-i) = i

Secara umum, nombor khayalan B ⋅ I dinaikkan ke kuasa n ialah:

(B jauh) iⁿ = bⁿ Yoⁿ = bⁿ i^(n mod 4)

Beberapa contoh adalah seperti berikut:

(5 i)¹² = 5¹² Yo¹² = 5¹² Yo⁰ = 5¹² x 1 = 244140625

(5 i)^sebelas = 5^sebelas Yo^sebelas = 5^sebelas Yo³ = 5^sebelas x (-i) = -48828125 i

(-2 i)¹⁰ = -2¹⁰ Yo¹⁰ = 2¹⁰ Yo² = 1024 x (-1) = -1024

Jumlah nombor sebenar dan satu khayalan

Apabila nombor sebenar ditambah dengan khayalan, hasilnya tidak nyata atau khayalan, ia adalah jenis baru yang dipanggil Nombor kompleks.

Sebagai contoh, jika x = 3.5 dan y = 3.75i, maka hasilnya adalah nombor kompleks:

Boleh melayani anda: dataran minimum

Z = x + y = 3.5 + 3.75 i

Perhatikan bahawa bahagian sebenar dan khayalan tidak dapat dikumpulkan dalam jumlah, jadi bilangan kompleks akan selalu mempunyai bahagian yang nyata dan bahagian khayalan yang lain.

Operasi ini memanjangkan set nombor sebenar kepada nombor yang paling luas.

Aplikasi

Nama nombor khayalan dicadangkan oleh ahli matematik Perancis René Descartes (1596-1650) sebagai penghinaan atau perselisihan dengan cadangan mereka yang dibuat oleh ahli matematik Itali Raffaelle Century Bombelli.

Ahli matematik yang hebat, seperti Euler dan Leibniz, meminjamkan Descartes dalam perselisihan ini dan dipanggil nombor khayalan sebagai nombor amfibia, yang dibahaskan antara menjadi dan ketiadaan.

Nama nombor khayalan dikekalkan hari ini, tetapi kewujudan dan kepentingannya sangat nyata dan terasa, kerana ia kelihatan secara semula jadi dalam banyak bidang fizik seperti:

-Teori Relativiti.

-Dalam elektromagnetisme.

-Mekanik kuantum.

Bersenam dengan nombor khayalan

- Latihan 1

Cari penyelesaian persamaan berikut:

z² + 16 = 0

Penyelesaian

z² = -16

Mengambil akar kuadrat pada kedua -dua ahli yang anda ada:

√ (z² ) = √ (-16)

± z = √ (-1 x 16) = √ (-1) √ (16) = i x 4 = 4i

Dengan kata lain, penyelesaian persamaan asal adalah:

z = +4i atau z = -4i.

- Latihan 2

Cari hasil menaikkan unit khayalan ke kuasa 5 tolak pengurangan unit khayalan yang dinaikkan ke kuasa -5.

Penyelesaian

Yo⁵ - Yo-⁵ = i⁵ - 1/i⁵ = i - 1/i = i - (i)/(i x i) = i - i/( - 1) = i + i = 2i

- Latihan 3

Cari hasil operasi berikut:

(3i)³ + 9i 

Penyelesaian

3³ Yo³ - 9 = 9 (-i) + 9i = -9i + 9i = 0i

- Latihan 4

Cari penyelesaian persamaan kuadrat berikut:

Boleh melayani anda: Teorem kewujudan dan keunikan: demonstrasi, contoh dan latihan

(-2x)² + 2 = 0

Penyelesaian

Persamaan disusun semula seperti berikut:

(-2x)² = -2

Kemudian ambil akar kuadrat pada kedua -dua ahli

√ ((-2x)²) = √ (-2)

± (-2x) = √ (-1 x 2) = √ (-1) √ (2) = i √ (2) = √2 i

Kemudian x akhirnya diperoleh:

x = ± √2 / 2 i

Iaitu, terdapat dua penyelesaian yang mungkin:

x = (√2 / 2) i

Atau yang lain:

x = - (√2 / 2) i

- Latihan 5

Cari nilai z yang ditakrifkan oleh:

Z = √ (-9) √ (-4) + 7

Penyelesaian

Kami tahu bahawa akar kuadrat nombor sebenar negatif adalah nombor khayalan, contohnya √ (-9) adalah sama dengan √ (9) x √ (-1) = 3i.

Sebaliknya, √ (-4) sama dengan √ (4) x √ (-1) = 2i.

Supaya persamaan asal dapat digantikan oleh:

3i x 2i - 7 = 6 i² - 7 = 6 (-1) -7 = -6 -7 = -13

- Latihan 6

Cari nilai z yang terhasil daripada bahagian berikut dua nombor kompleks:

Z = (9 - i²) / (3 + i)

Penyelesaian

Pengangka ungkapan boleh menjadi faktor menggunakan harta berikut:

Perbezaan kuadrat adalah hasil jumlahnya dengan perbezaan binomial tanpa menaikkan dataran.

Jadi:

Z = [(3 - i) (3 + i)] / (3 + i)

Ungkapan yang dihasilkan kemudian dipermudahkan dengan baki

Z = (3 - i)

Rujukan

1. Earl, r. Nombor kompleks. Pulih dari: matematik.lembu.Ac.UK.
2. Figuera, j. 2000. Matematik 1st. Dipelbagaikan. Edisi bersama.
3. Hoffmann, j. 2005. Pemilihan masalah matematik. Penerbitan Monfort.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Wikipedia. Nombor khayalan. Diperoleh dari: dalam.Wikipedia.org