Ciri -ciri Gelombang Senoid, Bahagian, Pengiraan, Contoh

The Gelombang Sine Mereka adalah corak gelombang yang boleh digambarkan secara matematik oleh fungsi sinus dan kosinus. Mereka betul -betul menggambarkan peristiwa semula jadi dan tanda -tanda yang berubah -ubah dalam masa, seperti voltan yang dihasilkan oleh tumbuhan elektrik dan kemudian digunakan di rumah, industri dan jalanan.

Unsur -unsur elektrik seperti rintangan, kapasitor dan induktansi, yang menyambung kepada input voltan sinusoidal, juga menghasilkan jawapan juga sinusoidal. Matematik yang digunakan dalam keterangan mereka agak mudah dan telah dikaji secara menyeluruh.

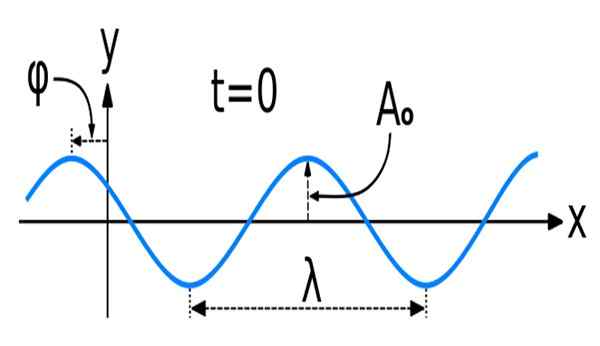
Rajah 1. Gelombang sinus dengan beberapa ciri spatial utamanya: amplitud, panjang gelombang dan fasa. Sumber: Wikimedia Commons. WAVE_NEW_SINE.SVG: Kraaiennestoriginally Dibuat sebagai Gelombang Cosine, oleh Pengguna: Pelegs, sebagai Fail: Wave_new.Kerja Svgderivative: Dave3457 [CC BY-SA 3.0 (https: // creativeCommons.Org/lesen/by-sa/3.0)]

Matematik gelombang sinusoidal atau sinusoidal, seperti yang diketahui, adalah fungsi sinus dan kosinus.

Ini adalah fungsi berulang, yang bermaksud berkala. Kedua -duanya mempunyai cara yang sama, dengan proviso bahawa kosinus dipindahkan ke kiri berkenaan dengan payudara di bilik kitaran. Ia diperhatikan dalam Rajah 2:

Rajah 2. Fungsi sen x dan cos x dipindahkan satu berkenaan dengan yang lain. Sumber: f. Zapata.

Kemudian cos x = sin (x + π/2). Dengan bantuan fungsi ini, gelombang sinus diwakili. Untuk melakukan ini, magnitud yang dimaksudkan diletakkan pada paksi menegak, sementara di paksi mendatar masa terletak.

Kualiti berulang fungsi ini juga dihargai pada graf di atas: corak diulang secara berterusan dan kerap. Terima kasih kepada fungsi -fungsi ini, anda dapat menyatakan voltan dan arus jenis Sinean yang berbeza -beza dari masa ke masa, meletakkan pada paksi menegak dan bukannya dan, a v atau satu Yo untuk mewakili voltan atau arus, dan pada paksi mendatar dan bukannya x, The t cuaca.

Cara paling umum untuk menyatakan gelombang sinus ialah:

v (t) = v_m dosa (Ωt+φ)

Kemudian kita akan memperdalam makna ungkapan ini, menentukan beberapa istilah asas untuk mencirikan gelombang sinus.

[TOC]

Pihak

Tempoh, amplitud, kekerapan, kitaran dan fasa adalah konsep yang digunakan untuk gelombang berkala atau berulang dan penting untuk mencirikannya dengan betul.

Tempoh

Fungsi berkala seperti yang disebutkan, yang diulangi secara berkala, selalu memenuhi harta berikut:

f (t) = f (t + t) = f (t + 2t) = f (t + 3t) = .. .

Di mana T Ia adalah jumlah yang dipanggil gelombang, Dan ini adalah masa yang diperlukan untuk mengulangi fasa yang sama. Dalam unit sistem antarabangsa, tempoh diukur dalam beberapa saat.

Amplitud

Menurut ungkapan umum gelombang senoid v (t) = v_m dosa (ωt+φ), v_m Ia adalah nilai maksimum fungsi, yang berlaku ketika dosa (ωt+φ) = 1 (Mengingat bahawa nilai terbesar yang fungsi sinus dan kosinus mengakui kedua -duanya adalah 1). Nilai maksimum ini adalah tepat Amplitud gelombang, juga dikenali sebagai amplitud puncak.

Sekiranya voltan akan diukur dalam volt dan jika ia adalah arus ia akan berada di amp. Dalam gelombang sinus, keluasan adalah malar, tetapi dalam jenis gelombang lain, amplitud boleh berbeza -beza.

Boleh melayani anda: termometer rintangan: ciri, operasi, kegunaan

Kitaran

Ia adalah sebahagian daripada gelombang yang terkandung dalam tempoh. Dalam angka sebelumnya, tempoh itu diambil dengan mengukurnya dari dua puncak atau rabung berturut -turut, tetapi ia boleh mula diukur dari bahagian lain gelombang, sementara ia dibatasi oleh suatu tempoh.

Perhatikan dalam angka berikut sebagai satu kitaran meliputi dari satu titik ke titik yang lain dengan nilai yang sama (ketinggian) dan cerun yang sama (kecenderungan).

Rajah 3. Dalam gelombang sinus, kitaran selalu berlaku untuk tempoh. Yang penting ialah titik permulaan dan akhir berada pada ketinggian yang sama. Sumber: Boylestad. Pengenalan kepada Analisis Litar. Pearson.

Kekerapan

Ia adalah jumlah kitaran yang berlaku dalam 1 saat dan dikaitkan dengan hujah fungsi sinus: ωt. Kekerapan dilambangkan sebagai F Dan ia diukur dalam kitaran sesaat atau Hertz (Hz) dalam sistem antarabangsa.

Kekerapan adalah jumlah terbalik tempoh, oleh itu:

F = 1/t

Sementara kekerapan F berkaitan dengan Kekerapan sudut Ω (denyutan) sebagai:

Ω = 2πF

Kekerapan sudut dinyatakan dalam radian /kedua dalam sistem antarabangsa, tetapi radians tidak dimensi, oleh itu kekerapan F dan kekerapan sudut Ω Mereka mempunyai dimensi yang sama. Perhatikan bahawa produk ωt Memberi radian sebagai hasilnya, dan mesti diambil kira apabila menggunakan kalkulator untuk mendapatkan nilai Sen ωt.

Fasa

Ia sepadan dengan anjakan mendatar yang dialami oleh gelombang, berkenaan dengan masa yang diambil sebagai rujukan.

Dalam angka berikut, gelombang hijau maju berkenaan dengan merah dalam satu masa t_d. Dua gelombang sinusoidal masuk fasa Apabila kekerapan dan fasa anda sama. Sekiranya fasa berbeza, maka mereka masuk jurang. Rajah 2 gelombang juga sudah lapuk.

Rajah 4. Pelued Sinusidal Waves. Sumber: Wikimedia Commons. Tiada pengarang yang boleh dibaca mesin yang disediakan. Kanjo ~ Commonswiki diasumsikan (berdasarkan tuntutan hak cipta). [Domain awam].

Sekiranya kekerapan gelombang berbeza, mereka akan berada dalam fasa apabila fasa ωt+φ sama dalam kedua -dua gelombang pada saat -saat tertentu.

Penjana Gelombang Senoid

Terdapat banyak cara untuk mendapatkan isyarat berbentuk sinus. Runnings buatan sendiri memberikan mereka.

Permohonan undang -undang Faraday

Cara yang agak mudah untuk mendapatkan isyarat sinus adalah menggunakan undang -undang Faraday. Ini menunjukkan bahawa dalam litar tertutup arus, contohnya gelung, diletakkan di tengah -tengah medan magnet, arus yang diinduksi dihasilkan apabila medan magnet mengalir melalui ia berubah dari masa ke masa. Akibatnya, a Voltan yang disebabkan Sama ada FEM yang disebabkan.

Aliran medan magnet berbeza -beza jika gelung diputar dengan kepantasan sudut tetap di tengah -tengah medan yang dibuat antara tiang n dan s magnet yang ditunjukkan dalam angka.

Boleh melayani anda: Neptune (planet)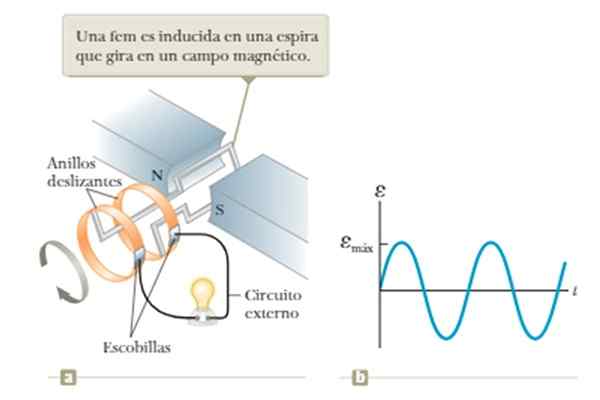Rajah 5. Penjana Gelombang Berdasarkan Undang -undang Induksi Faraday. Sumber: Sumber: Raymond a. Serway, Jonh W. Jewett [cc by-sa 4.0 (https: // creativeCommons.Org/lesen/by-sa/4.0)].

Batasan pengendali ini adalah pergantungan pada voltan yang diperoleh dengan kekerapan putaran gelung, seperti yang akan dilihat dengan lebih terperinci dalam Contoh 1 bahagian contoh kemudian.

Wien Oscillator

Cara lain untuk mendapatkan gelombang sinus, kali ini dengan elektron. Dengan cara ini, gelombang sinus diperolehi kekerapan dan amplitud yang pengguna dapat mengubah suai mengikut kemudahan mereka, dengan cara pelarasan suis.

Angka ini menunjukkan penjana isyarat sinus, yang mana bentuk gelombang lain juga boleh diperolehi: segi tiga dan kuadrat antara lain.

Rajah 6. Penjana isyarat. Sumber: Sumber: Wikimedia Commons. Opgreg di Bahasa Inggeris Wikipedia [CC BY-SA 3.0 (https: // creativeCommons.Org/lesen/by-sa/3.0)].

Cara mengira gelombang sinus?

Untuk melakukan pengiraan yang melibatkan gelombang sinus, kalkulator saintifik digunakan yang mempunyai fungsi sinus dan kosinus trigonometri, serta songsangnya. Kalkulator ini mempunyai mod untuk mengerjakan sudut sama ada dalam darjah atau radian, dan mudah untuk menukar satu cara ke yang lain. Faktor penukaran adalah:

180 º = π Radianes.

Menurut model kalkulator, anda mesti menavigasi melalui kekunci mod untuk mencari pilihan ijazah, yang membolehkan anda bekerja pada fungsi trigonometri dalam darjah, atau pilihan rad, untuk terus bekerja sudut dalam radianes.

Contohnya dosa 25 º = 0.4226 dengan kalkulator dimasukkan ke dalam mod deg. Dengan menukar 25 º ke radians anda mendapat 0.4363 Radianes dan Sen 0.4363 rad = 0.425889 ≈ 0.4226.

Oscilloscope

Oscilloscope adalah radas yang membolehkan untuk memvisualisasikan pada tanda -tanda skrin voltan dan arus kedua -dua alternatif dan langsung. Ia mempunyai tombol untuk menyesuaikan saiz isyarat pada grid seperti yang ditunjukkan dalam angka berikut:

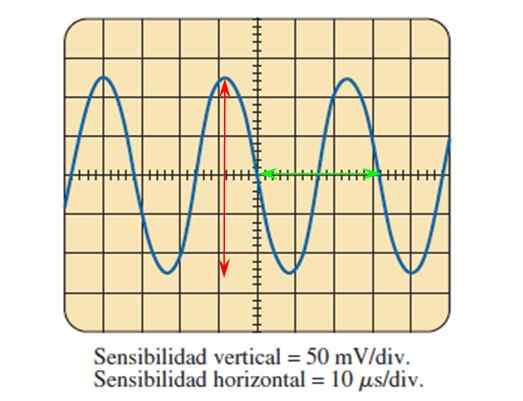Rajah 7. Isyarat sinusoidal yang diukur dengan osiloskop. Sumber: Boylestad.

Melalui imej yang disediakan oleh osiloskop dan mengetahui pelarasan kepekaan dalam kedua -dua paksi, adalah mungkin untuk mengira parameter gelombang yang diterangkan di atas.

Boleh melayani anda: galaksi elips: pembentukan, ciri, jenis, contoh

Angka ini menunjukkan isyarat voltan sinus sebagai fungsi masa, di mana setiap pembahagian paksi menegak bernilai 50 millivolts, manakala dalam paksi mendatar, setiap bahagian bernilai 10 mikroseconds.

Puncak ke puncak amplitud menghitung bahagian yang gelombang merangkumi secara menegak, membantu dengan anak panah merah:

5 Bahagian dikira dengan bantuan anak panah merah, jadi voltan puncak-pico adalah:

V_ms = 5 bahagian x 50 mV/bahagian = 250 mV.

Voltan pico V_p Ia diukur dari paksi mendatar, iaitu 125 mV.

Untuk mencari tempoh kitaran diukur, contohnya yang dibatalkan oleh anak panah hijau, yang meliputi 3.2 bahagian, maka tempohnya adalah:

T = 3.2 Bahagian x 10 Microseconds/Division = 32 Microseconds = 32 μs

Contoh

Contoh 1

Untuk penjana dalam Rajah 3, tunjukkan dari undang -undang Faraday bahawa voltan yang diinduksi mempunyai sinus. Anggapkan bahawa gelung terdiri daripada N bertukar bukannya satu, semuanya dengan kawasan yang sama A dan beralih dengan kepantasan sudut tetap Ω di tengah -tengah medan magnet B seragam.

Penyelesaian

Undang -undang Faraday mengatakan bahawa FEM yang diinduksi ε adalah:

ε = -n (dφ_B /dt)

Di mana Φ_B Ia adalah aliran medan magnet, yang akan berubah, kerana ia bergantung pada bagaimana gelung itu terdedah kepada medan setiap saat. Tanda negatif hanya menerangkan hakikat bahawa fem ini menentang punca yang menghasilkannya (undang -undang Lenz). Aliran disebabkan oleh satu gelung adalah:

Φ_B = B.Ke.cos θ

θ adalah sudut bahawa vektor normal ke satah gelung terbentuk dengan medan B Apabila putaran berlaku (lihat angka), sudut ini secara semula jadi berbeza sebagai:

θ = ωt

Jadi itu: Φ_B = B.Ke.cos θ = b.Ke.cos ωt. Sekarang anda hanya perlu mendapatkan ungkapan ini berkenaan dengan masa dan dengan itu FEM yang diinduksi diperoleh:

ε = -n.d (b.Ke.cos Ωt) /dt

Seperti medan B Ia seragam dan kawasan spase tidak berbeza -beza, mereka meninggalkan derivatif:

ε = -NBA. D (cos ωt) /dt = ωnba. Sen ωt

Contoh 2

Gelung mempunyai kawasan 0.100 m² dan bertukar menjadi 60.0 rev/s, dengan paksi putaran tegak lurus ke medan magnet seragam 0.200 t. Mengetahui bahawa gegelung mempunyai 1000 giliran untuk mencari: a) FEM maksimum yang dihasilkan, b) orientasi gegelung berhubung dengan medan magnet apabila FEM yang diinduksi maksimum berlaku.

Rajah 8. Lingkaran pusingan N yang rosak di tengah -tengah medan magnet seragam dan menghasilkan isyarat sinus. Sumber: r. Serway, Fizik untuk Sains dan Kejuruteraan. Jilid 2. Pembelajaran Cengage.

Penyelesaian

a) FEM maksimum adalah ε_Maks = Ωnba

Sebelum meneruskan untuk menggantikan nilai, kekerapan 60 rev/s ke unit sistem antarabangsa mesti diluluskan. Telah diketahui bahawa 1 revolusi bersamaan dengan radian giliran atau 2p:

60.0 Rev/S = 120p Radianes/S

ε_Maks = 120p Radianes x 1000 pusingan x 0.200 t x 0.100 m² = 7539.82 V = 7.5 kV

b) Apabila nilai ini berlaku Sen ωt = 1 Oleh itu:

ωt = θ = 90º,

Dalam kes ini, pesawat lingkaran selari dengan B, Jadi vektor biasa untuk kata pesawat membentuk 90º dengan medan. Ini berlaku apabila vektor hitam dalam Rajah 8 berserenjang dengan vektor hijau yang mewakili medan magnet.

Rujukan

1. Boylestad, r. 2011. Pengenalan kepada Analisis Litar. Ke -12. Edisi. Pearson. 327-376.
2. Figueroa, d. 2005. Elektromagnetisme. Siri Fizikal untuk Sains dan Kejuruteraan. Jilid 6. Diedit oleh d. Figueroa. Simon Bolivar University. 115 dan 244-245.
3. Figueroa, d. 2006. Makmal Fizik 2. Equinox editorial. 03-1 dan 14-1.
4. Gelombang Sine. Pulih dari: iessierradegara.com
5. Serway, r. 2008.Fizik untuk Sains dan Kejuruteraan. Jilid 2. Pembelajaran Cengage. 881-884