Matematik

Pasangan yang diperintahkan

Pasangan yang diperintahkan

Apa itu pasangan yang teratur?

Pasangan yang teratur atau DUO Ia adalah satu set dua elemen yang ditulis mengikut perintah yang ditetapkan oleh kriteria tertentu. Kriteria tersebut menyatakan yang mana dari kedua -dua elemen itu berjalan terlebih dahulu dan yang mana yang berlaku.

Pasangan yang diperintahkan dilambangkan sebagai (x, y), di mana "x" adalah elemen pertama pasangan dan "y" adalah yang kedua, juga dipanggil Komponen. Secara umum (x, y) ia bukan tork rapi yang sama (y, x). Dan sebagai tambahan kepada perintah itu, satu lagi ciri penting pasangan yang diperintahkan adalah kesamaan: dua pasangan yang diperintahkan (a, b) dan (c, d) adalah sama hanya jika a = c dan b = d = d.

Rajah 1.- Terima kasih kepada pasangan yang kemas, anak anjing tahu bahawa tulang dikebumikan di lokasi (3,1) dan (-4,2), sementara rumahnya berada di (0.0). Sumber: f. Zapata.

Contoh pasangan yang diperintahkan adalah yang terdiri daripada umur dan berat kursus pelajar matematik. Pasangan yang diperintahkan (15, 62) sepadan dengan pelajar 15 tahun, berbeza dengan pasangan yang tidak mungkin (62,15).

Konsep tork yang diperintahkan sangat penting dalam pelbagai bidang matematik, seperti pesawat Cartesian, pecahan, vektor dalam satah, hubungan dan fungsi. Aspek penting ialah unsur -unsur mereka tidak semestinya mempunyai berangka, sebagai contoh, mereka boleh dipesan dengan:

  • Negara bandar
  • Nama nama belakang
  • Suami isteri

Dan banyak kombinasi lain.

Contoh pasangan yang diperintahkan

Pecahan

Pecahan diwakili sebagai kuota dua bilangan bulat P/Q, contohnya pecahan ½, yang bersamaan dengan nombor perpuluhan 0.5.

Walau bagaimanapun, pecahan ini bukan satu -satunya yang mewakili perpuluhan 0.5, begitu juga dengan perkara berikut:

2/4; 3/6; (-2)/(-4); 20/40; (-1)/(-2) ..

Dengan cara ini, mana -mana pecahan boleh diwakili sebagai pasangan yang teratur (p, q), di mana p dan q adalah keseluruhan, dengan p menduduki kedudukan pengangka dan q yang penyebutnya. Terdapat sekatan penting dan q (penyebut) harus berbeza dari 0, kerana pecahan borang P/0 tidak ditakrifkan.

Boleh melayani anda: set terhingga: sifat, contoh, latihan yang diselesaikan

Dan satu lagi keadaan penting ialah dua pecahan A/B dan C/D adalah sama selagi ia dipenuhi:

A ∙ d = b ∙ c

Fungsi dan grafnya

Fungsi boleh dinyatakan sebagai satu set pasangan yang kemas. Sebagai contoh, dengan grafik fungsi dalam pesawat Cartesian, elemen pertama diberikan kedudukan pemboleh ubah bebas, sementara yang kedua diberikan pemboleh ubah bergantung. Ini adalah pasangan yang teratur.

Untuk fungsi y = f (x), tork rapi boleh dinyatakan sebagai [x, f (x)]]. Sebagai contoh, pertimbangkan set permulaan:

A = 1, 2, 3, 4

Dalam set ini terdapat komponen pertama pasangan teratur mengikut fungsi y = x2. Set komponen kedua ialah:

B = 1, 4, 9, 16

Dan pasangan yang diperintahkan terbentuk adalah:

(1,1); (2,4); (3, 9); (4; 16)

Menganggap.

Vektor dalam kapal terbang

Vektor boleh diwakili dalam satah Cartesian oleh pasangan yang diperintahkan, di mana elemen pertama mewakili komponen mendatar "x" dan kedua komponen menegak "Y". Untuk membezakan vektor dari titik dalam pesawat, mereka dilambangkan oleh huruf tebal dan kurungan persegi digunakan bukannya tanda kurung, seperti ini:

v =

Contohnya, vektor v = mempunyai komponen mendatar sama dengan 4 dan komponen menegak bersamaan dengan 7. Grafnya adalah:

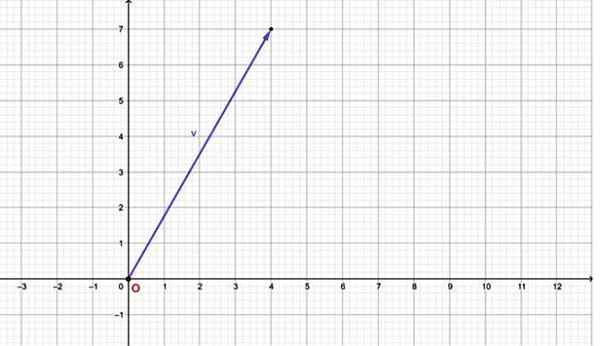Rajah 2.- Vektor pesawat boleh dinyatakan melalui pasangan yang teratur. Sumber: f. Zapata.

Perhatikan bahawa vektor ini mempunyai asalnya bertepatan dengan asal sistem koordinat (0.0). Sekiranya vektor mempunyai asalnya di mana -mana titik lain, ia juga boleh dinyatakan dalam bentuk tork yang teratur melalui pasangan yang teratur, untuk berbuat demikian melihat bahagian berikut.

Boleh melayani anda: hierarki operasi

Memerintahkan operasi Pares

Tambahan

Biarkan sasaran (a, b) dan (c, d) menjadi pasangan (d). Tork baru diperoleh melalui jumlahnya mengikut:

(a, b)+(c, d) = (a+c, b+d)

Elemen neutral

Unsur neutral penambahan pasangan yang diperintahkan adalah tork (0.0), kerana ketika ia menambah pasangan yang diperintahkan (a, b), jumlahnya adalah yang terakhir:

(a, b) + (0.0) = (a, b)

Jumlah yang bertentangan

Dengan menambah pasangan yang teratur (a, b) dengan bertentangan (-a, -b) tork teratur (0.0) diperoleh:

(a, b) + (-a, -b) = (0.0)

Komutatif

Perintah penambahan tidak mengubah jumlahnya:

(a, b) + (c, d) = (c, d) + (a, b)

Bersekutu

Hasil menambahkan tiga pasangan yang diperintahkan tidak diubah apabila dikumpulkan untuk melaksanakan operasi:

[(a, b) + (c, d)] + (e, f) = (a, b) + [(c, d) + (e, f)]

Penolakan pasangan yang diperintahkan

Biarkan sasaran (a, b) dan (c, d) menjadi, penolakan dilakukan seperti berikut:

(a, b)-(c, d) = (a-c, b-d)

Produk

Dalam produk terdapat dua pilihan: i) melipatgandakan tork yang diperintahkan oleh malar dan ii) membiak dua (atau lebih) tidies.

Pendaraban dengan pemalar

Biarkan k menjadi tork yang berterusan dan teratur (a, b), produk antara pemalar dan tork adalah:

K ∙ (a, b) = (k ∙ a, k ∙ b)

Pendaraban pasangan yang diperintahkan

Produk antara pasangan yang diperintahkan (a, b) dan (c, d) dijalankan seperti berikut:

(a, b) x (c, d) = (ac - bd, bc+ad)

Elemen neutral

Unsur pendaraban neutral adalah (1.0), kerana dengan mendarabkan sebarang tork yang diperintahkan oleh ini, berikutan peraturan pendaraban yang diterangkan di atas, tork asal adalah:

(a, b) x (1.0) = (a - 0, b + 0) = (a, b)

Boleh melayani anda: songsang berbilang: penjelasan, contoh, latihan yang diselesaikan

Bersekutu

Oleh kerana urutan faktor tidak mengubah produk, ia boleh dikumpulkan dengan cara yang berbeza untuk membiak tiga atau lebih pasangan yang kemas dan hasilnya adalah sama:

[(a, b) x (c, d)] x (e, f) = (a, b) x [(c, d) x (e, f)]

Latihan yang diselesaikan

Latihan 1

Anda telah memesan pasangan (x2, X-2) = (16, 2). Yang merupakan nilai x?

Penyelesaian

Memohon kesamaan pasangan yang diperintahkan diperoleh terlebih dahulu:

x2 = 16 ⇒ x1 = 4, x2 = -4

Untuk mengetahui yang mana kedua -dua nilai memilih, penggunaan:

X-2 = 2

x = 2 + 2 = 4

Oleh itu, nilai x yang diminta ialah 4.

Latihan 2

Ekspres sebagai pasangan teratur vektor yang pergi dari titik (1, 3) ke titik (7, 11) dan mewakilinya secara grafik.

Penyelesaian

Menjadi v Vektor mencari. Untuk menentukan pasangan yang teratur yang mewakilinya, dan yang mengandungi koordinatnya, koordinat titik ketibaan dan titik asal dikurangkan, mengikut urutan itu. Jadi:

v = =

Vektor kemudiannya diwakili v seperti yang keluar dari (1.3) hingga (7, 11) dan peralatan v yang asalnya ditetapkan kepada asal sistem koordinat (0.0). Seperti yang anda lihat, mereka mempunyai arah dan makna yang sama.

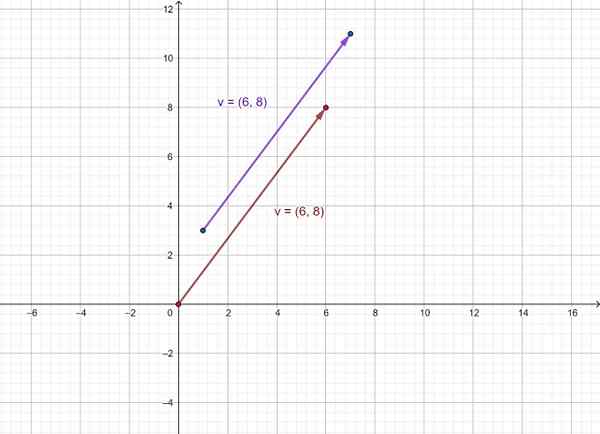Rajah 3. Perwakilan vektor sebagai pasangan teratur. Sumber: f. Zapata.

Rujukan

  1. Deepal. Pasangan yang diperintahkan. Pulih dari: Deepai.org.
  2. Mathemovil. Perwakilan Cartesian vektor oleh pasangan yang teratur. Pulih dari: Matemovil.com.
  3. Varsity Tutorrs. Pasangan yang diperintahkan. Diperolehi dari: WarSityTorm.com
  4. Priestri, Juan. Hubungan dan fungsi. Fakulti Kejuruteraan. Jabatan Matematik. Universiti Buenos Aires. Diperolehi dari: Subjek.fi.Uba.ar.
  5. Universiti Denver. Hubungan. Pulih dari: matematik.Ucdenver.Edu.