Elemen Pentadecágono, Klasifikasi, Ciri, Latihan

A Pentadecantagon Ia adalah angka rata yang dibina dengan lima belas segmen lurus dan ditutup. Angka semacam ini dipanggil poligon dan mereka dinamakan mengikut jumlah pihak yang ada.

Segitiga, dengan tiga sisi dan kuadrilateral, empat, adalah contoh poligon yang sangat biasa, tetapi poligon mungkin mempunyai lebih banyak sisi.

Rajah 1.  Pentagon biasa dengan simpang merah. Sumber: Wikimedia Commons.

Unsur -unsur asas pentadecágono adalah sama dengan mana -mana poligon, tanpa mengira jumlah sisi yang dimilikinya. Unsur -unsur ini adalah:

-Sisi, yang merupakan segmen yang membentuk pentadecágono dengan jumlah 15.

-Simpang, Juga 15, yang merupakan hujung sisi bersebelahan.

-Sudut dalaman, Mereka yang terbentuk di dalam pentadecágono antara dua sisi bersebelahan.

-Sudut luaran, dibentuk di antara satu sisi dan pemanjangan salah satu sisi berturut -turut.

-Diagonal, Segmen garis yang menyertai dua simpang yang tidak bersekongkol.

[TOC]

Klasifikasi

Pentadecágono boleh biasa Sama ada tidak teratur, Bergantung pada saiz sisi mereka dan ukuran sudut dalamannya. Sekiranya anda mempunyai semua sisi dan sudut dalaman yang sama -quilátero dan equiangle - ia adalah biasa, seperti yang ditunjukkan dalam Rajah 1, jika tidak, ia tidak teratur.

Ia juga boleh dikelaskan sebagai cembung Sama ada cekung. Pentagon cekung mempunyai satu atau lebih sudut dalaman yang lebih besar daripada 180º, sementara yang selalu cembung mempunyai sudut dalaman kurang dari 180º. Pentagon biasa adalah cembung.

Kriteria klasifikasi lain dianggap jika sisi tidak berturut -turut - atau sambungan mereka - dipotong atau tidak. Apabila mereka tidak dipotong, seperti dalam hal Rajah 1, dikatakan bahawa ia adalah pentadecágon yang mudah. Dan jika mereka dipotong, maka itu kompleks.

Ia dapat melayani anda: geometri analisis

Pentagon biasa

Pentagon biasa, yang sisi dan sudut dalamannya mempunyai ukuran yang sama, adalah tokoh simetri yang hebat, kerana unsur -unsur tambahan berikut ditakrifkan kepada yang digambarkan sebelumnya:

-Pusat: Titik yang menyamakan kedudukan dan sisi.

-Radio: Jarak dari pusat ke salah satu simpang pentagon biasa.

-Sudut pusat: Orang yang mempunyai puncaknya di tengah -tengah angka dan sisinya melewati dua simpang bersebelahan.

-Apothem, Ia adalah segmen tegak lurus yang bergabung dengan pusat satu sisi dengan pusat angka.

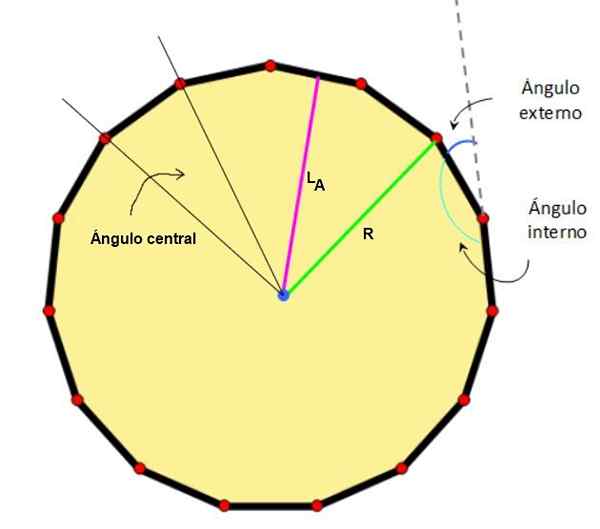Rajah 2. Pusat, apothem, radio dan sudut yang ketara dari pentadecágono. Sumber: Wikimedia Commons/F. Zapata.

- Ciri -ciri pentagon biasa

Sudut dalaman

Formula berikut digunakan untuk mengira ukuran I sudut dalaman mana -mana poligon biasa, di mana n Ia adalah bilangan sisi:

Dalam formula ini, ukuran saya datang dalam darjah, untuk menyatakannya dalam radian, ia didarabkan oleh faktor π/180. Mari lihat apakah ukuran sudut dalaman pentagon biasa, menggantikan n = 15:

I = [(15-2) × 180º]/15 = 156º

Bersamaan dengan 13π/15 radian. Oleh kerana sudut dalaman pentagon biasa kurang dari 180º, ia adalah poligon cembung.

Jumlah sudut dalaman

Adalah mungkin untuk mengira jumlah sudut dalaman menggunakan formula berikut:

S = (n-2) x 180º

Seperti biasa, n mewakili bilangan sisi. Formula ini sah untuk n = 3, 4, 5 .. .

Melakukan n = 15 kita dapat:

S = (15 - 2) x 180º = 2340º

Sudut luaran

Sudut dalaman dan sudut luaran adalah tambahan, iaitu jumlahnya adalah 180º, seperti yang dinyatakan dalam Rajah 2. Oleh itu, sudut luaran langkah pentadecágono:

Boleh melayani anda: Binomial konjugasi: Bagaimana ia diselesaikan, contoh, latihan

180 º - 156º = 24º.

Perimeter dan kawasan

Perimeter adalah ukuran kontur poligon dan mudah menambahkan semua sisi. Yeah ke Ia adalah panjang sisi, sudah cukup untuk membiak oleh n, Bilangan sisi.

Untuk pentagon biasa A, perimeter p ialah:

P = 15a

Sekiranya ia adalah angka yang tidak teratur, di mana ukuran sisi berbeza, perimeter menambahkan panjang semua sisinya.

Bagi kawasan itu, kita boleh mengira dalam beberapa cara. Sebagai contoh, kami mempunyai formula yang membolehkan anda mendapatkannya mengetahui panjang A dari sisinya:

Melaksanakan operasi yang ditunjukkan, ia tetap kira -kira:

A = 17,6426 ⋅²

Terdapat pilihan lain, terpakai bagi poligon biasa. Ia adalah mengenai membahagikannya ke segitiga asas sama dengan poligon. Ketinggian segitiga adalah panjang apothem l_Ke, ditakrifkan di atas.

Kawasan segitiga tersebut dikira dengan formula yang terkenal: ketinggian x asas /2. Dengan cara ini kawasan segitiga tunggal adalah:

Kawasan = a. L_Ke /2

Untuk mempunyai jumlah kawasan poligon, sudah cukup untuk membiak dengan bilangan sisi n, yang dalam kes ini adalah 15:

A = 15 ⋅ a l_Ke /2

Dan kerana perimeter angka itu adalah p = 15 ⋅ a, maka:

A = P ⋅ l_Ke /2

Diagonal

Diagonal adalah segmen yang menyatukan dua simpang bukan berkonsepkan, seperti yang dinyatakan di atas. Untuk mengetahui berapa banyak pepenjuru poligon biasa n Sisi, termasuk Pentadecágono, terdapat formula berikut:

Di mana d adalah bilangan pepenjuru.

Sekarang kita menggantikan n = 15, untuk mendapatkan jumlah pepenjuru:

Boleh melayani anda: poligon biasa: sifat, elemen, sudut, contoh

D = [15 × (15-3)]/2 = 90 pepenjuru.

Pembinaan dengan peraturan dan kompas

Pentadecágono dibina dengan peraturan dan kompas bermula dari lilitan. 360º mesti dibahagikan kepada 15 bahagian yang sama 24º. Pertama pembinaan tambahan yang ditunjukkan dalam animasi dijalankan untuk mendapatkan sudut 60º, yang dibahagikan kepada 36º dan 24º.

Rajah 3. Pembinaan dengan peraturan dan kompas pentagon biasa. Sumber: Wikimedia Commons.

Latihan diselesaikan

Sekiranya perimeter pentadecágono didaftarkan dalam lingkaran radius r ialah 12.56 cm. Kira:

a) radio.

b) kawasan anda.

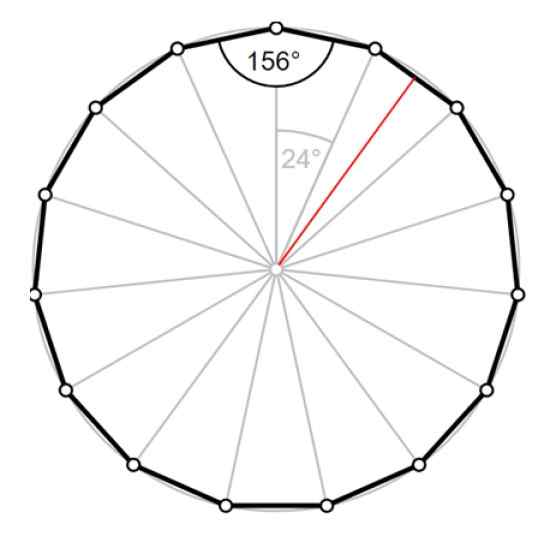Rajah 4. Pentadecágono: Sudut Tengah, Sudut Dalaman dan Apothema Merah. Sumber: Wikimedia Commons/F. Zapata.

Penyelesaian kepada

Perimeter adalah p = 15 ⋅ a = 12.Oleh itu, 56 cm sebelah Pentadecágono adalah 0.8373 cm. Radio Kita boleh mengira dengan bantuan salah satu segitiga dalam Rajah 4.

Apothem l_Ke sepadan dengan ketinggian segitiga, ditarik merah, yang membahagikan sudut 24º menjadi dua sudut 12º setiap satu.

Terdapat dua segitiga yang betul dengan sudut dalaman 12º setiap satu, dan kepada mana -mana daripada mereka kita boleh menggunakan trigonometri untuk mencari hipotenus, iaitu panjang r radius.

Cara ini:

sen 12º = (a /2) /r

R = (a /2) /sen 12º = (0.8373 cm / 2) / sen12º = 2.01 cm.

Penyelesaian b

Kita boleh mengira kawasan Pentadecágono menggunakan formula:

A = P ⋅ l_Ke /2

Kita sudah tahu perimeter p = 12.56 cm, dan panjang apotem dikira oleh tangen atau 12º cosine:

Cos 12º = l_Ke / R

L_Ke = R. cos 12 º = 2.01 cm. cos 12 º = 1.97 cm

Mengganti:

A = 12.56 cm ⋅ 1.97 cm /2 = 12.35 cm²

Rujukan

1. Alexander, d. 2013. Geometri. 5th. Edisi. Pembelajaran Cengage.
2. Belajar matematik. Angka geometri. Pulih dari: Rodrigoanchorena.Wixsite.com.
3. Matematik Sangaku. Unsur poligon dan klasifikasinya. Pulih dari: Sangakoo.com.
4. Wikipedia. Pentadecágono. Pulih dari: Adakah.Wikipedia.org.
5. Wolfram Math World. Pentadecagon. Pulih dari: Mathworld.Wolfram.com.