Pesawat Cartesian

Apa itu kapal terbang Cartesian?

Dia Pesawat Cartesian Ia terdiri daripada sepasang garis lurus yang berserenjang antara satu sama lain dan bersilang pada satu ketika. Salah satu garis adalah menegak dan yang lain mendatar, mengambil ke titik persimpangan sebagai asal sistem.

Matlamatnya adalah dengan mudah mencari titik rata melalui sepasang nilai: menyelaras. Untuk melakukan ini, pada setiap baris skala dengan nombor keseluruhan dibina, yang positif ditulis dalam satu arah dan negatif di sisi lain, seperti yang ditunjukkan dalam angka berikut:

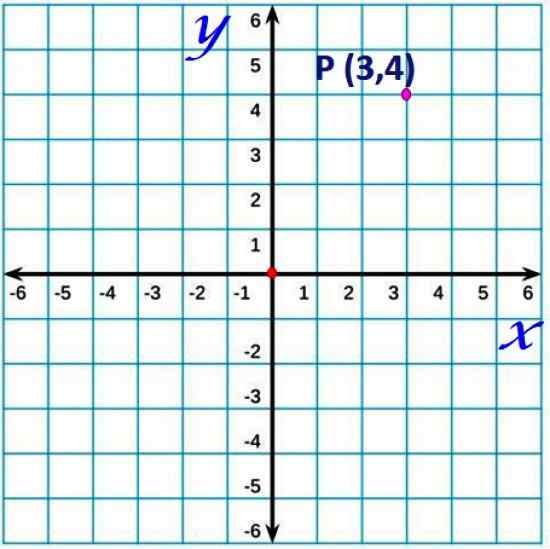
Rajah 1. Titik dalam pesawat Cartesian. Sumber: f. Zapata.

Oleh konvensyen, paksi mendatar biasanya dipanggil x dan paksi menegak sebagai paksi dan.

Mana -mana titik pesawat akan mempunyai koordinat yang ditentukan oleh pasangan yang teratur (X, y). Sebagai contoh, titik P koordinat (3,4), terletak 3 unit di sebelah kanan asal dan 4 unit, di atas angka. Ia serupa dengan peta, yang menunjukkan latitud dan panjang lokasi tertentu.

Oleh kerana dua koordinat diperlukan, dikatakan bahawa pesawat itu adalah dua dimensi, tetapi konsepnya mudah dilanjutkan kepada tiga dimensi, menambah paksi lebih banyak koordinat, yang biasanya dilambangkan sebagai paksi z. Dalam kes ini, koordinat terbentuk (X dan z).

Pesawat Cartesian menerima namanya dari saintis Perancis René Descartes (1596-1650), yang memformalkannya dalam karyanya Ucapan kaedah Dari 1637, walaupun terdapat sejarah dalam karya Apollonius Perga (262-190 AC), ahli matematik yang menemui lengkung kerucut: lilitan, elips, perumpamaan dan hiperbola.

Boleh melayani anda: Perbezaan kiub: formula, persamaan, contoh, latihan

Ciri -ciri Pesawat Cartesian

- Seperti dia X paksi Sebagai Paksi y Mereka meluas di kedua -dua hujungnya, dan bersilang bersama -sama (pada sudut 90 darjah). Ciri ini dipanggil orthogonality.

- Titik di mana kedua -dua paksi bersilang dikenali sebagai asal atau titik sifar.

- Sistem koordinat membahagikan pesawat ke empat wilayah yang disebut kuadran.

- Lokasi dalam satah koordinat digambarkan sebagai pasangan yang diperintahkan.

- Setiap titik di pesawat Cartesian dikaitkan dengan koordinat x yang unik dan koordinat dan unik.

Unsur -unsur pesawat Cartesian

Unsur -unsur pesawat Cartesian adalah seperti berikut:

-The garis berangka Sama ada Menyelaras paksi x dan y, Sekiranya itu kapal terbang. Paksi dan Terima nama paksi ordinat, sementara paksi x Ia adalah paksi abscissa. Ketika datang ke ruang angkasa, maka paksi ditambah z, dapat mewakili ketinggian dan kedalaman.

-Dia asal, yang merupakan titik persimpangan paksi.

-The kuadran, yang merupakan kawasan yang ditentukan oleh paksi koordinat pada satah dan dikira dalam arah yang bertentangan dengan tangan jam, bermula dengan kuadran pertama. Mereka ditakrifkan seperti berikut:

• Kuadran pertama: paksi x dan dan positif.
• Kuadran kedua: sepadan dengan paksi x negatif dan paksi positif dan positif.
• Kuadran Ketiga: Ia mempunyai kedua -dua paksi negatif.
• Kuadran Keempat: Dengan paksi x positif dan paksi negatif dan negatif.

Umumnya, kuadran dilambangkan dalam nombor Rom, seperti ini:

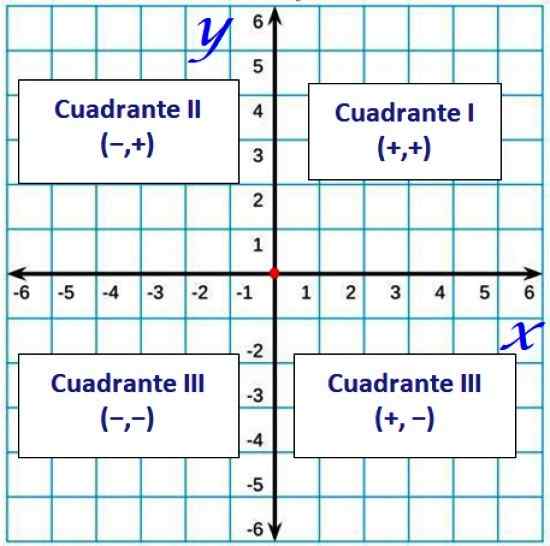Rajah 2. Cuadrants dalam pesawat Cartesian. Sumber: f. Zapata.

Dipesan pasangan dan jarak antara dua mata

Pasangan yang diperintahkan adalah koordinat setiap titik, di mana koordinat x selalu diletakkan terlebih dahulu, seperti dalam contoh Rajah 1. Koordinat (3,4) titik p menunjukkan bahawa x = 3 dan y = 4.

Dalam angka lain di bawah ini, titik P milik kuadran IV dan mempunyai koordinat (2; -1.5). Perhatikan bahawa dengan memproyeksikan garis dari paksi koordinat ke titik p membentuk segi empat tepat. Inilah sebab mengapa koordinat Cartesian juga dipanggil Koordinat segi empat tepat.

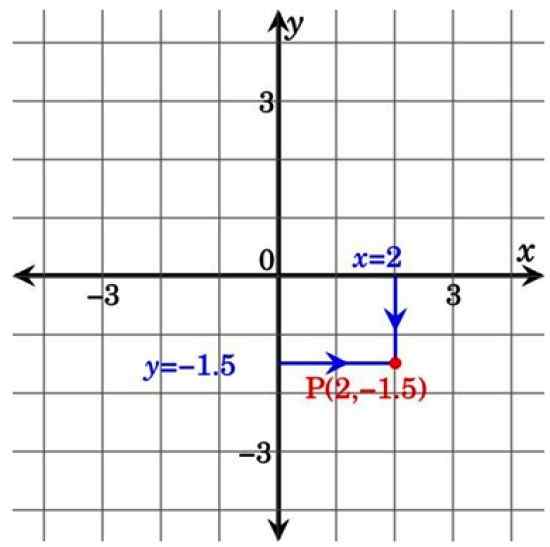Rajah 3. Menunjuk pada pesawat Cartesian. Sumber: Wikimedia Commons.

Aplikasi Plane Cartesian

Pesawat Cartesian mempunyai banyak aplikasi dalam banyak bidang. Pada mulanya, Descartes memperkenalkannya kepada lengkung lengkung lengkung dalam satah, itulah sebabnya ia dianggap sebagai bapa geometri analisis.

Boleh melayani anda: Produk Cruz

Walau bagaimanapun, penggunaannya meliputi semua jenis hubungan dan fungsi, seperti:

-Ikuti trajektori badan dengan pergerakan parabola, bulat atau curvilinear secara umum.

-Secara grafik menentukan cara di mana dua pembolehubah berkaitan melalui fungsi.

-Cari mata di tanah rata untuk memudahkan pengukuran pada mereka.

Rujukan

1. Matematik menyeronokkan. Koordinat Cartesian. Pulih dari: MathSisfun.com/data/koordinat Cartesian.
2. Pesawat Cartesian. Diperolehi dari: DL.Uncw.Edu.