Sifat poligon biasa, elemen, sudut, contoh

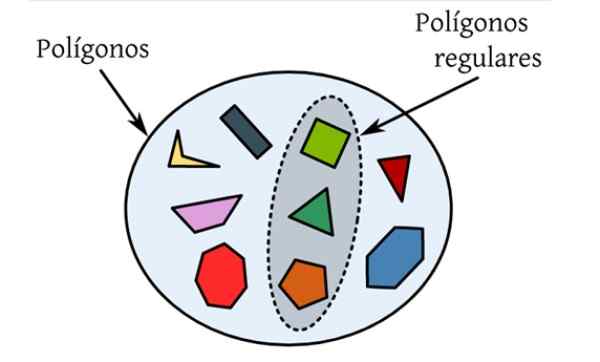
The poligon biasa Mereka adalah mereka yang mempunyai semua sisi dan sudut dalaman mereka yang sama. Dalam angka berikut terdapat satu set poligon yang berbeza, yang merupakan angka rata yang terhad oleh lengkung tertutup dan hanya yang diserlahkan memenuhi syarat -syarat yang biasa.

Sebagai contoh, segitiga sama rata adalah poligon biasa, kerana tiga sisinya mengukur sama, serta sudut dalamannya, yang bernilai 60 º setiap satu.

Rajah 1. Poligon biasa adalah mereka yang sisi dan sudut dalamannya adalah sama, seperti segitiga sama rata dan dataran. Sumber: Wikimedia Commons.

Dataran adalah segi empat dengan empat sisi ukuran yang sama dan sudut dalamannya adalah 90º. Diikuti oleh pentagon biasa, dengan lima sisi saiz yang sama dan lima sudut dalaman 108º.

Apabila poligon biasa, perkataan ini ditambah kepada nama khasnya, oleh itu kita mempunyai segi enam biasa, heptagon biasa dan sebagainya.

[TOC]

Sifat poligon biasa

Ciri -ciri terpenting poligon biasa dapat diringkaskan seperti berikut:

-Sisi mengukur sama, oleh itu mereka keseimbangan.

-Adalah Equiagular, Nah, semua sudut dalamannya mempunyai ukuran yang sama.

-Mereka sentiasa boleh mendaftar di lilitan, yang bermaksud bahawa mereka sesuai dengan sempurna, yang dipanggil Circumference.

-Untuk poligon biasa N sisi, ukuran sudut dalaman α ialah:

α = [180 (n-2)]/n

-N-3)/2 pepenjuru boleh diambil dari simpul poligon, sama ada biasa atau tidak.

-Jumlah sudut luaran Ia sama dengan 360º.

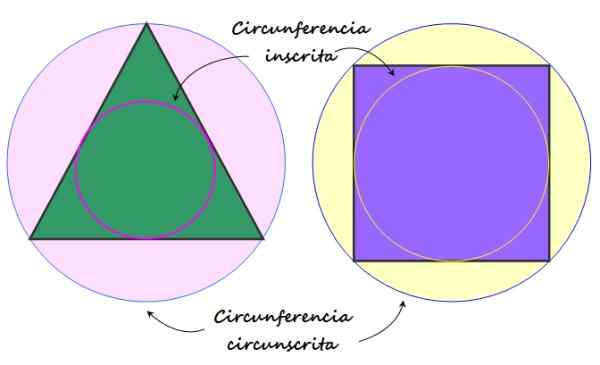Rajah 2. Lilitan dan lilitan berdaftar yang dilampirkan kepada poligon biasa. Sumber: f. Zapata.

Unsur poligon biasa

Kemudian kami membentangkan unsur -unsur utama poligon biasa, digambarkan dalam angka yang lebih rendah.

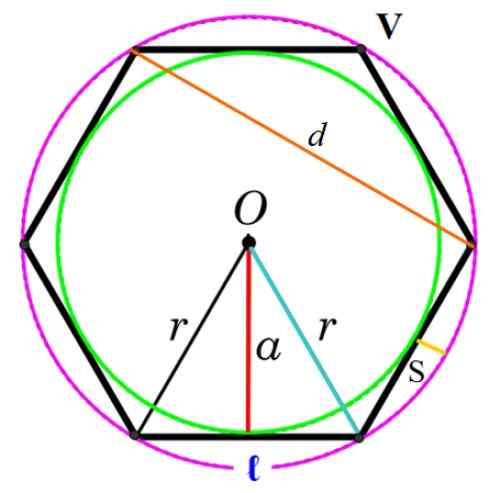Rajah 3. Unsur poligon biasa. Sumber: f. Zapata.

Puncak

Titik umum yang mempunyai dua sisi berturut -turut, dilambangkan sebagai v dalam angka.

Sisi

Ia adalah segmen yang bergabung dengan dua titik berturut -turut poligon dan dilambangkan sebagai ℓ atau l.

Pepenjuru

Segmen yang bergabung dengan dua simpang bukan poligon, dalam angka itu dilambangkan sebagai d.

Pusat

Ia adalah pusat umum lilitan berdaftar dan lilitan yang dilampirkan, dilambangkan oleh surat atau. Ia juga dapat dilihat sebagai satu -satunya titik bahawa equidista dari kedua -dua simpang dan titik tengah di setiap sisi.

Radio

Ia adalah radio r dari lilitan yang dilampirkan dan bertepatan dengan jarak antara O dan puncak.

Ia boleh melayani anda: Aksioma Kebarangkalian: Jenis, Penjelasan, Contoh, Latihan

Apothem

Ia dikenali sebagai Apothem kepada jejari lilitan yang ditulis dalam poligon, yang diwakili dalam angka dengan huruf ke. Apothem berserenjang ke sisi dan menyatukannya dengan pusat O (segmen merah dalam Rajah 3).

Mengetahui radius r dan panjang sisi, apothem dikira oleh:

Oleh kerana, pada dasarnya, apothem adalah salah satu kategori segitiga segi empat tepat (lihat Rajah 3), Cateto yang lain menjadi nilai ℓ/2 (separuh satu sisi) dan hypotenuse radio r daripada poligon.

Apabila teorem Pythagoras digunakan untuk segitiga tersebut, persamaan ini diperolehi, yang sah bukan sahaja untuk segi enam, tetapi bagi mana -mana poligon biasa.

Sudut pusat

Ia adalah sudut yang puncaknya bertepatan dengan pusat atau sisinya adalah segmen yang menyatukan pusat dengan dua simpul berturut -turut. Ukurannya dalam darjah sexagesimal adalah 360º/n, di mana n Ia adalah jumlah sisi poligon.

Sagita

Ia adalah perbezaan antara jejari poligon dan apothem (lihat Rajah 3). Menandakan sagita sebagai s:

S = r - a

Perimeter dan kawasan

Perimeter

Ia mudah dikira dengan menambahkan panjang sisi. Seperti mana -mana pihak adalah panjang yang sama l dan terdapat N sisi, perimeter p dinyatakan sebagai:

P = n.L

Kawasan

Dalam poligon biasa, kawasan A diberikan oleh produk antara separuh perimeter (separuh perimeter) dan panjang apothem ke.

A = p.A /2

Oleh kerana perimeter bergantung kepada bilangan sisi n, ternyata:

A = (NL).A /2

Dua poligon biasa boleh mempunyai perimeter yang sama walaupun mereka tidak mempunyai bilangan sisi yang sama, kerana ia akan bergantung pada panjang sisi.

Dalam buku V anda Koleksi, Ahli matematik Pappus dari Alexandria (290-350), yang terakhir dari ahli matematik Yunani yang hebat, menunjukkan bahawa di antara semua poligon biasa dengan perimeter yang sama, yang mempunyai kawasan yang paling besar adalah yang paling besar.

Sudut

Rajah 4 menunjukkan sudut yang relevan dalam poligon biasa, dilambangkan dengan huruf Yunani α, β dan γ.

Sudut pusat

Sebelum ini kita menyebut sudut tengah, di antara unsur -unsur poligon biasa, ia adalah sudut yang puncaknya berada di tengah poligon dan sisi adalah segmen yang menyatukan pusat dengan dua titik berturut -turut.

Untuk mengira ukuran sudut pusat α, 360º dibahagikan dengan n, bilangan sisi. Atau 2 π radian antara n:

Boleh melayani anda: fungsi injective: apa yang terdiri daripada, apa itu dan contohnya

α = 360º/n

Bersamaan dengan radian ke:

α = 2π /n

Sudut dalaman atau sudut dalaman

Dalam Rajah 4 sudut dalaman β adalah yang puncaknya bertepatan dengan salah satu angka dan sisinya adalah sisi angka juga. Ia dikira dalam ijazah sexagesimal oleh:

β = [180 (n-2)]/n

Atau di radians menggunakan:

β = [π (n-2)]/n

Sudut luaran

Mereka dilambangkan oleh huruf Yunani γ. Dalam angka itu diperhatikan bahawa γ + β = 180º. Oleh itu:

γ = 180º - β

Jumlah semua sudut luaran ke poligon biasa ialah 360º.

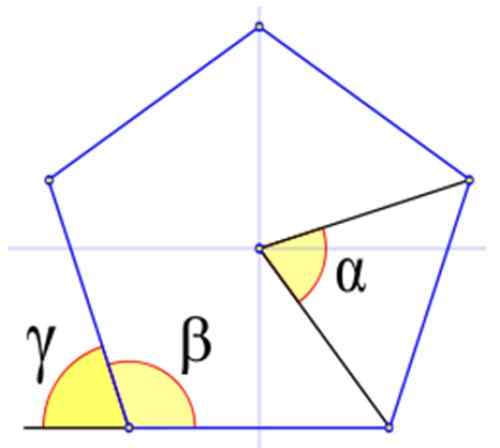Rajah 4. Sudut dalam poligon biasa, dalam contoh ini pentagon biasa. Sumber: Wikimedia Commons.

Contoh poligon biasa

Di bawah ini kita mempunyai 8 poligon biasa yang pertama. Kami memerhatikan bahawa apabila bilangan pihak meningkat, poligon menjadi semakin banyak ke lilitan di mana mereka didaftarkan.

Kita dapat membayangkan bahawa membuat panjang sisi semakin kecil, dan meningkatkan bilangan ini, kita mendapat lilitan.

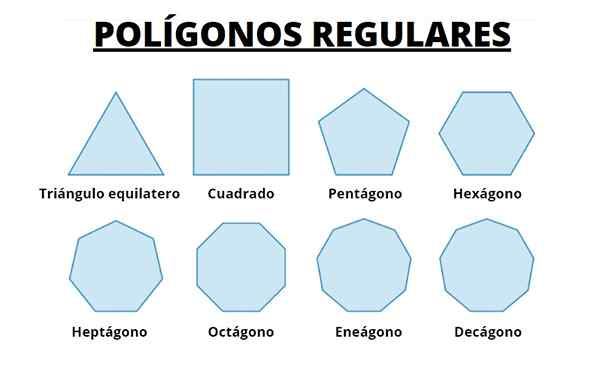Rajah 5. Lapan poligon biasa pertama. Sumber: Wikimedia Commons.

- Poligon biasa dalam kehidupan seharian dan alam semula jadi

Poligon biasa dijumpai di mana -mana dalam kehidupan seharian dan juga di alam. Mari lihat beberapa contoh:

Isyarat lalu lintas

Dalam papan tanda yang kita lihat di lebuh raya dan jalan raya berlimpah poligon biasa seperti segitiga sama, persegi dan rhombus. Dalam Rajah 6 kita melihat isyarat isyarat berbentuk tinggi.

Rajah 5.- Isyarat lalu lintas dengan bentuk segi tiga. Sumber: Pixabay.

Perabot

Potongan perabot yang tidak terhitung misalnya, sebagai angka geometri ciri, serta banyak meja, kerusi dan bank adalah persegi. Parallelepiped biasanya kotak dengan sisi segi empat tepat (yang bukan poligon biasa), tetapi mereka juga boleh membuat persegi.

Senibina dan Pembinaan

Jubin atau jubin lantai dan dinding, baik di rumah dan di jalanan, sering mempunyai bentuk poligon biasa.

Tesel adalah permukaan yang diliputi sepenuhnya dengan jubin yang mempunyai angka geometri yang pelbagai. Dengan segitiga, dataran dan segi enam boleh dibuat tesselves biasa, mereka yang menggunakan hanya satu jenis angka untuk salutan dengan sempurna, tanpa ruang kosong (lihat Rajah 6).

Juga bangunan menggunakan poligon biasa dalam elemen seperti tingkap dan hiasan.

Rajah 6. Jubin persegi. Sumber: Pixabay.

- Hexagons biasa

Menghairankan, Hexagon biasa adalah poligon yang sering muncul dalam alam semula jadi.

Boleh melayani anda: pengagihan diskret

Honeycombs yang dibuat oleh lebah untuk menyimpan madu mempunyai bentuk yang sangat anggaran untuk segi enam biasa. Seperti yang diperhatikan oleh pappus Alexandria, dengan cara ini lebah mengoptimumkan ruang untuk menjimatkan sebanyak mungkin madu.

Dan terdapat juga heksagon biasa di cengkerang penyu dan kepingan salji, yang juga mengamalkan pelbagai bentuk geometri yang sangat indah.

Latihan diselesaikan

Hexagon biasa adalah sebahagian daripada separuh bulatan radius 6 cm, seperti yang ditunjukkan dalam angka tersebut. Berapakah nilai kawasan yang berlorek?

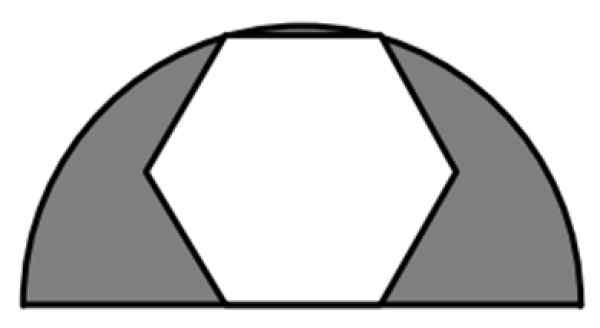Rajah 7. Hexagon biasa yang didaftarkan di separuh bulatan. Sumber: f. Zapata.

Penyelesaian

Kawasan yang berlorek adalah perbezaan antara kawasan separuh bulatan radius r = 6 cm dan kawasan heksagon penuh, poligon tetap 6 orang biasa. Oleh itu, kita memerlukan formula untuk kawasan setiap angka ini.

Kawasan separuh bulatan

Ke₁ = π r² /2 = π (6 cm)² /2 = 18π cm²

Kawasan heksagon biasa

Formula untuk mengira kawasan poligon biasa adalah:

A = p.A /2

Di mana P Ia adalah perimeter dan ke Ia adalah apothem. Oleh kerana perimeter adalah jumlah sisi, kita memerlukan nilai ini. Untuk segi enam biasa:

P = 6 ℓ

Oleh itu:

A = 6 ℓa /2

Untuk mencari nilai sampingan ℓ adalah perlu untuk membina angka tambahan, yang akan kita jelaskan di bawah:

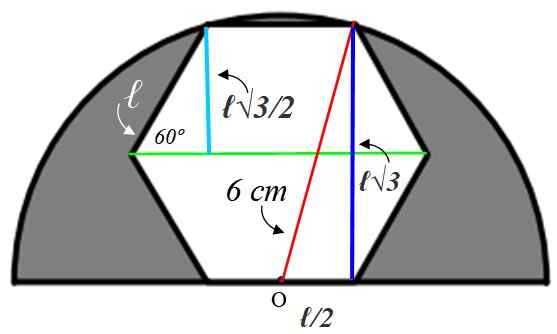
Mari kita mulakan dengan segitiga segi empat tepat kecil di sebelah kiri, yang hipotenus ℓ. Sudut dalaman heksagon bernilai:

α = [180 (n-2)]/n = α = [180 (6-2)]/6 = 120º

Radius yang telah kita tarik di Bisecta Green sudut ini, oleh itu sudut akut segitiga kecil adalah 60º. Dengan maklumat yang diberikan, segitiga ini diselesaikan, mencari sisi biru muda, yang mengukur sama seperti apothem:

Cateto bertentangan = a = ℓ x sin 60º = ℓ√3 / 2 cm

Nilai ini adalah dua kali ganda kaki biru gelap segitiga besar ke kanan, tetapi dari segitiga itu kita tahu bahawa hipotenus berukuran 6 cm kerana ia adalah radius separuh bulatan. Cateto yang tinggal (di bawah) bernilai ℓ/2 sejak titik atau berada di bahagian tengah.

Oleh kerana sudut dalaman segitiga ini tidak diketahui, kita dapat menaikkan teorem Pythagoras untuknya:

36 = 3 ℓ² + ℓ² / 4

(13/4) ℓ² = 36 → ℓ = √ (4 x36) /13 cm = 12 /√13 cm

Dengan nilai ini, apothem dikira:

A = ℓ√3 /2 cm = (12 /√13) x (√3 /2) cm = 6√3 /√13 cm

Mari panggil a₂ ke kawasan heksagon biasa:

= 28. 8 cm²

Kawasan angka yang berlorek

Ke₁ - Ke₂ = 18π cm²  - 28.8 cm² = 27.7 cm²

Rujukan

1. Baldor, a. 1973. Geometri dan trigonometri. Editorial Kebudayaan Amerika Tengah.
2. Nikmati matematik. Tesel. Pulih dari: nikmatMatimaticas.com.
3. Dan. Ke. 2003. Elemen Geometri: Dengan Latihan dan Geometri Kompas. Universiti Medellin.
4. Hexagons dalam Alam. Pulih dari: malvargamath.WordPress.com.
5. Jiménez, r. 2010. Matematik II. Geometri dan trigonometri. Edisi kedua. Prentice Hall.
6. Poligon biasa. Pulih dari: pasangan.kejuruteraan.USAC.Edu.Gt.
7. Wikipedia. Apothem. Pulih dari: Adakah.Wikipedia.org.