Formula dan persamaan kebarangkalian bersyarat, sifat, contoh

The kebarangkalian bersyarat Kemungkinan kejadian kejadian tertentu, kerana yang lain terjadi sebagai suatu keadaan. Maklumat tambahan ini dapat mengubah suai (atau mungkin tidak) persepsi bahawa sesuatu akan berlaku.

Sebagai contoh, kita boleh bertanya kepada diri sendiri: "Apakah kebarangkalian hujan hari ini, sejak dua hari yang lalu tidak hujan?". Acara yang kita ingin tahu kebarangkalian adalah hujan hari ini, dan maklumat tambahan yang akan memberi jawapan adalah bahawa "dua hari yang lalu ia tidak hujan".

Rajah 1. Kebarangkalian hujan hari ini sejak hujan semalam juga merupakan contoh kebarangkalian bersyarat. Sumber: Pixabay.

Menjadi Ruang probabilistik terdiri daripada Ω (ruang sampel), ℬ (peristiwa rawak) dan p (kebarangkalian setiap peristiwa), ditambah peristiwa a dan b yang tergolong dalam ℬ.

Kebarangkalian yang dikondisikan yang berlaku, kerana B, yang dilambangkan sebagai P (A│b), ditakrifkan dengan cara ini:

P (a│b) = p (a∩b) / p (b) = p (a dan b) / p (b)

Di mana: p (a) adalah kebarangkalian kejadian a, p (b) adalah kebarangkalian peristiwa b dan berbeza dari 0, dan p (a∩b) adalah kebarangkalian persimpangan antara a dan b, iaitu , kebarangkalian bahawa kedua -dua peristiwa berlaku (kebarangkalian bersama).

Ini adalah ungkapan untuk teorem Bayes yang digunakan untuk dua peristiwa, yang dicadangkan pada tahun 1763 oleh ahli teologi Inggeris dan ahli matematik Thomas Bayes.

[TOC]

Sifat

-Semua kebarangkalian bersyarat antara 0 dan 1:

0 ≤ p (a│b) ≤ 1

-Kebarangkalian bahawa peristiwa akan berlaku, kerana peristiwa ini berlaku, jelas 1:

P (a│a) = p (a∩a) / p (a) = p (a) / p (a) = 1

-Jika dua peristiwa adalah eksklusif, iaitu, peristiwa yang tidak boleh berlaku secara serentak, maka kebarangkalian bersyarat yang salah satu daripada mereka berlaku adalah 0, kerana persimpangan itu tidak sah:

P (a│b) = p (a∩b) / p (b) = 0 / p (b) = 0

-Jika B adalah subset A, maka kebarangkalian bersyarat juga 1:

Boleh melayani anda: Toroid atau Toro Dona

P (b│a) = p (a∩b) / p (a) = 1

Penting

P (a│b) ia biasanya tidak sama dengan p (b│a), oleh itu anda perlu berhati -hati untuk tidak bertukar peristiwa apabila mencari kebarangkalian bersyarat.

Peraturan pendaraban umum

Banyak kali anda ingin mencari kebarangkalian bersama p (a∩b), bukan kebarangkalian bersyarat. Oleh itu, melalui teorem berikut yang anda ada:

P (a∩b) = p (a dan b) = p (a│b). P (b)

Teorem boleh diperluaskan untuk tiga acara A, B dan C:

P (a∩b∩c) = p (a dan b dan c) = p (a) · p (b│a) · p (c│a∩b)

Dan juga untuk beberapa acara, seperti₁, Ke₂, Ke₃ Dan banyak lagi, ia boleh dinyatakan seperti berikut:

P (a₁∩ a₂ ∩ a₃... ∩ A_n) = P (a₁) . P (a₂│A₁). P (a₃│A₁∩ a₂) ... p (a_n│A₁∩ a₂∩ ... a_N-1)

Apabila ia adalah kes peristiwa yang berlaku dalam urutan dan melalui peringkat yang berbeza, mudah untuk mengatur data dalam rajah atau jadual. Ini memudahkan menggambarkan pilihan untuk mencapai kebarangkalian yang diminta.

Contohnya adalah Rajah pokok dan juga Jadual kontingensi. Dari salah seorang daripada mereka, anda boleh membina yang lain.

Contoh kebarangkalian bersyarat

Mari kita lihat beberapa situasi di mana kebarangkalian peristiwa diubah oleh kejadian yang lain:

- Contoh 1

Di kedai manis dua jenis kek dijual: strawberi dan coklat. Apabila mendaftarkan keutamaan 50 pelanggan kedua -dua jantina, nilai -nilai berikut ditentukan:

-27 wanita, di mana 11 lebih suka strawberi dan 16 kek coklat.

-23 lelaki: 15 coklat dan 8 strawberi.

Kebarangkalian bahawa pelanggan memilih kek coklat dapat ditentukan dengan menggunakan peraturan Laplace, mengikut kebarangkalian apa -apa peristiwa adalah:

P = bilangan peristiwa yang menggalakkan/jumlah peristiwa

Dalam kes ini, daripada 50 pelanggan, sejumlah 31 lebih suka coklat, sehingga kebarangkalian akan p = 31/50 = 0.62. Iaitu, 62% pelanggan lebih suka kek coklat.

Boleh melayani anda: persamaan polinomial

Tetapi adakah ia berbeza jika pelanggan adalah seorang wanita? Ini adalah kes kebarangkalian bersyarat.

Jadual kontingensi

Melalui jadual kontingensi seperti ini, jumlahnya mudah digambarkan:

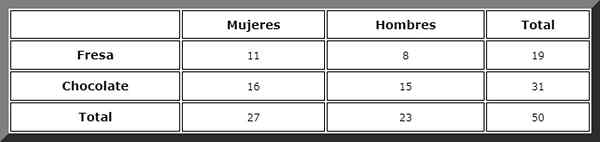
Kemudian kes -kes yang menggalakkan diperhatikan dan peraturan Laplace digunakan, tetapi sebelum kita menentukan peristiwa:

-B adalah acara "Pelanggan Wanita".

-A adalah acara "lebih suka kek coklat" menjadi wanita.

Kami pergi ke lajur yang dilabel "wanita" dan di sana kita melihat bahawa jumlahnya adalah 27.

Kemudian kes yang menggalakkan dicari dalam baris "coklat". Terdapat 16 peristiwa ini, oleh itu kebarangkalian yang dicari secara langsung:

P (a│b) = 16/27 = 0.5924

A 59.24 % wanita wanita lebih suka kek coklat.

Nilai ini bertepatan apabila kita berbeza dengan definisi kebarangkalian bersyarat pada mulanya:

P (a│b) = p (a∩b) / p (b)

Kami memberi jaminan kepada diri kami melalui peraturan Laplace dan nilai -nilai jadual:

P (B) = 27/50

P (A dan B) = 16/50

Di mana p (a dan b) adalah kebarangkalian pelanggan lebih suka coklat dan wanita. Sekarang nilai diganti:

P (a│b) = p (a dan b)/p (b) = (16/50)/(27/50) = 16/27 = 0.5924.

Dan terbukti bahawa hasilnya sama.

- Contoh 2

Dalam contoh ini, peraturan pendaraban terpakai. Katakan bahawa dalam pameran kedai terdapat seluar dalam tiga saiz: kecil, sederhana dan besar.

Banyak dengan jumlah seluar 24, di mana terdapat 8 dari setiap saiz dan semuanya bercampur. Apa kebarangkalian mengekstrak dua daripadanya dan kedua -duanya adalah kecil?

Sudah jelas bahawa kebarangkalian mengekstrak seluar kecil dalam percubaan pertama ialah 8/24 = 1/3. Sekarang, pengekstrakan kedua dikondisikan ke acara pertama, kerana ketika anda mengeluarkan seluar, tidak ada lagi 24, tetapi 23. Dan jika seluar kecil dikeluarkan, terdapat 7 bukannya 8.

Boleh melayani anda: Prinsip Multiplicative: Mengira Teknik dan Contoh

Acara A adalah dengan mengeluarkan seluar kecil, setelah mengambil satu lagi dalam percubaan pertama. Dan acara B adalah seluar kecil yang pertama. Oleh itu:

P (b) = 1/3; P (a│b) = 7/24

Akhirnya, melalui peraturan pendaraban:

P (a∩b) = (7/24).(1/3) = 7/72 = 0.097

Latihan diselesaikan

Dalam kajian ketepatan masa mengenai penerbangan udara komersial, data berikut boleh didapati:

-P (b) = 0.83, adalah kebarangkalian bahawa kapal terbang mengambil masa yang tepat.

-P (a) = 0.81, adalah kebarangkalian pendaratan tepat pada waktunya.

-P (b∩a) = 0.78 adalah kebarangkalian bahawa penerbangan akan tiba tepat pada masanya mengambil masa yang tepat.

Diminta untuk mengira:

a) Apakah kebarangkalian pesawat terbang segera sejak ia dimulakan tepat pada waktunya?

b) Kebarangkalian di atas adalah sama dengan kebarangkalian bahawa ia telah keluar tepat pada waktunya jika anda berjaya mendarat dengan segera?

c) dan akhirnya: apakah kebarangkalian bahawa ia akan tiba tepat pada waktunya kerana ia tidak keluar tepat pada waktunya?

Rajah 2. Ketepatan masa penerbangan komersial adalah penting, kerana kelewatan menjana kerugian jutawan. Sumber: Pixabay.

Penyelesaian kepada

Untuk menjawab soalan, definisi kebarangkalian bersyarat digunakan:

P (a│b) = p (a∩b) / p (b) = p (a dan b) / p (b) = 0.78/0.83 = 0.9398

Penyelesaian b

Dalam kes ini, peristiwa ditukar dalam definisi:

P (b│a) = p (a∩b) / p (a) = p (a dan b) / p (a) = 0.78/0.81 = 0.9630

Perhatikan bahawa kebarangkalian ini sedikit berbeza dari yang sebelumnya, seperti yang telah kami nyatakan sebelum ini.

Penyelesaian c

Kebarangkalian tidak tepat waktu adalah 1 - p (b) = 1 - 0.83 = 0.17, kita akan memanggilnya p (b^C), Kerana ia adalah peristiwa pelengkap untuk mengambil masa yang tepat. Kebarangkalian bersyarat yang dicari adalah:

P (a│b^C) = P (a∩b^C) / P (b^C) = P (a dan b^C)/P (b^C)

Sebaliknya:

P (a∩b^C) = P (pendaratan masa) - p (pendaratan masa dan mengintip) = 0.81-0.78 = 0.03

Dalam kes ini, kebarangkalian yang dicari adalah:

P (a│b^C) = 0.03/0.17 = 0.1765

Rujukan

1. Canavos, g. 1988. Kebarangkalian dan Statistik: Aplikasi dan Kaedah. McGraw Hill.
2. DEVORE, J. 2012. Kebarangkalian dan statistik untuk kejuruteraan dan sains. Ke -8. Edisi. Cengage.
3. Lipschutz, s. 1991. Siri Schaum: Kebarangkalian. McGraw Hill.
4. Obregón, i. 1989.Teori kebarangkalian. Editorial Limusa.
5. Walpole, r. 2007. Kebarangkalian dan statistik untuk kejuruteraan dan sains. Pearson.
6. Wikipedia. Kebarangkalian terkondisi. Pulih dari: Adakah.Wikipedia.org.