Konsep kebarangkalian kekerapan, bagaimana dikira dan contoh

The Kebarangkalian kekerapan adalah sub-definisi dalam kajian kebarangkalian dan fenomena. Kaedah kajiannya berkenaan dengan peristiwa dan atribut, didasarkan pada jumlah lelaran yang banyak, dengan itu memerhatikan masing -masing dalam jangka panjang atau bahkan pengulangan yang tidak terhingga.

Contohnya, sampul gummitan mengandungi 5 karet setiap warna: biru, merah, hijau dan kuning. Anda ingin menentukan kebarangkalian bahawa setiap warna terpaksa meninggalkan selepas pemilihan rawak.

Sumber: Pexels

Ia membosankan untuk membayangkan mendapatkan getah, merekodkannya, mengembalikannya, mengeluarkan getah dan mengulangi beberapa ratus atau ribu kali yang sama. Anda juga boleh melihat tingkah laku selepas beberapa juta lelaran.

Tetapi sebaliknya, ia menarik untuk ditemui, bahawa selepas beberapa pengulangan kebarangkalian yang diharapkan sebanyak 25% tidak dipenuhi sepenuhnya, sekurang -kurangnya bukan untuk semua warna selepas 100 lelaran berlaku.

Di bawah pendekatan kebarangkalian kekerapan, peruntukan nilai hanya melalui kajian banyak lelaran. Dengan cara ini proses mesti dijalankan dan lebih baik didaftarkan secara berkomputer atau dicontohi.

Pelbagai arus menolak kebarangkalian kekerapan, dengan alasan kekurangan empiris dan kebolehpercayaan dalam kriteria rawak.

[TOC]

Bagaimana kebarangkalian kekerapan dikira?

Apabila pengaturcaraan eksperimen di mana -mana antara muka yang mampu menawarkan lelaran semata -mata rawak, anda boleh mula mengkaji kebarangkalian kekerapan fenomena melalui jadual nilai.

Contoh sebelumnya dihargai dari pendekatan kekerapan:

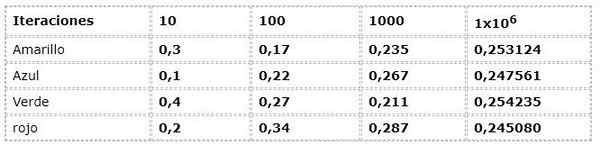
Data berangka sesuai dengan ungkapan:

N (a) = bilangan kejadian/ bilangan lelaran

Di mana n (a) mewakili kekerapan relatif peristiwa "a"

"A" tergolong dalam set hasil yang mungkin atau ruang sampel Ω

Ia dapat melayani anda: gandaan 8: Apa dan penjelasan

Ω: merah, hijau, biru, kuning

Terdapat penyebaran yang besar dalam lelaran pertama, apabila frekuensi dengan sehingga 30% perbezaan diperhatikan antara satu sama lain, yang merupakan fakta yang sangat tinggi untuk eksperimen yang secara teorinya mempunyai peristiwa dengan kemungkinan yang sama (equiprobable).

Tetapi apabila lelaran berkembang, nilai -nilai kelihatan semakin banyak kepada yang dibentangkan oleh arus teoretikal dan logik.

Undang -undang nombor besar

Sebagai perjanjian yang tidak dijangka antara pendekatan teoretikal dan kekerapan, undang -undang jumlah besar timbul. Di mana ia ditubuhkan bahawa selepas jumlah lelaran yang besar, nilai -nilai eksperimen kekerapan menghampiri nilai teoritis.

Contohnya, anda dapat melihat bagaimana nilai dianggarkan kepada 0.250 apabila lelaran berkembang. Fenomena ini adalah asas dalam kesimpulan banyak karya probabilistik.

Sumber: Pexels

Pendekatan kebarangkalian lain

Terdapat 2 teori atau pendekatan lain untuk tanggapan kebarangkalian sebagai tambahan kepada Kebarangkalian kekerapan.

Teori logik

Pendekatan anda berorientasikan kepada logik deduktif fenomena. Dalam contoh sebelumnya kebarangkalian mendapatkan setiap warna adalah 25% ditutup. Dalam kata lain.

Teori subjektif

Ia berdasarkan pengetahuan dan kepercayaan sebelumnya bahawa setiap individu mempunyai mengenai fenomena dan atribut. Pernyataan seperti "Ia selalu hujan di Suci Minggu " Mereka mematuhi corak peristiwa serupa yang telah berlaku sebelum ini.

Sejarah

Permulaan tarikh pelaksanaannya dari abad kesembilan belas, ketika saya mengutipnya dalam beberapa karyanya di Cambridge England. Tetapi tidak sampai abad kedua puluh bahawa 2 matematik statistik berkembang dan dibentuk Kebarangkalian kekerapan.

Boleh melayani anda: persamaan polinomial

Salah seorang daripada mereka ialah Hans Reichenbach, yang mengembangkan karyanya dalam penerbitan seperti "Teori Kebarangkalian" yang diterbitkan pada tahun 1949.

Yang lain ialah Richard von Mises, yang mengembangkan karyanya dengan lebih teliti melalui pelbagai penerbitan dan dicadangkan untuk mempertimbangkan kebarangkalian sebagai sains matematik. Konsep ini baru dalam matematik dan akan menandakan permulaan era pertumbuhan dalam kajian Kebarangkalian kekerapan.

Sebenarnya acara ini membuat satu -satunya perbezaan dengan sumbangan yang dibuat oleh penjanaan Venn, Counot dan Helm. Di mana kebarangkalian menjadi rakan sejawatan seperti geometri dan mekanik.

< La teoría de las probabilidades trata con fenomena besar dan peristiwa berulang. Masalah di mana peristiwa yang sama diulang lagi dan lagi, atau sebilangan besar unsur seragam yang terlibat pada masa yang sama> Richard von Mises

Fenomena besar dan peristiwa berulang

Tiga jenis boleh diklasifikasikan:

• Fizik: Corak alam semulajadi melampaui keadaan rawak. Contohnya tingkah laku molekul elemen dalam sampel.
• Peluang: Pertimbangan asasnya adalah rawak, seperti dengan melepaskan dadu berulang kali.
• Statistik Biologi: Pilihan Subjek Ujian Menurut Ciri dan Atribut mereka.

Dalam teori, individu yang mengukur memainkan peranan dalam data probabilistik, kerana ia adalah pengetahuan dan pengalamannya yang menyatakan nilai atau ramalan ini.

Di dalam Kebarangkalian kekerapan Acara akan dianggap sebagai koleksi yang akan dirawat, di mana individu tidak memainkan peranan dalam anggaran.

Atribut

Dalam setiap elemen atribut berlaku, yang akan berubah mengikut sifat ini. Sebagai contoh, dalam jenis fenomena fizikal, molekul air akan mempunyai kelajuan yang berbeza.

Ia dapat melayani anda: Kriteria persamaan segi tiga

Dalam pelancaran dadu kita tahu ruang sampel Ω yang mewakili atribut eksperimen.

Ω: 1, 2, 3, 4, 5, 6

Terdapat atribut lain seperti Ω_P  atau ganjil Ω_Yo

Ω_p : 2, 4, 6

Ω_Yo : 1, 3, 5

Yang boleh ditakrifkan sebagai atribut bukan selaras.

Contoh

• Anda ingin mengira kekerapan setiap jumlah yang mungkin dalam pelancaran dua dadu.

Untuk ini, eksperimen diprogramkan di mana dua nilai rawak antara [1, 6] ditambah dalam setiap lelaran.

Data dicatatkan dalam jadual dan trend dalam jumlah besar dikaji.

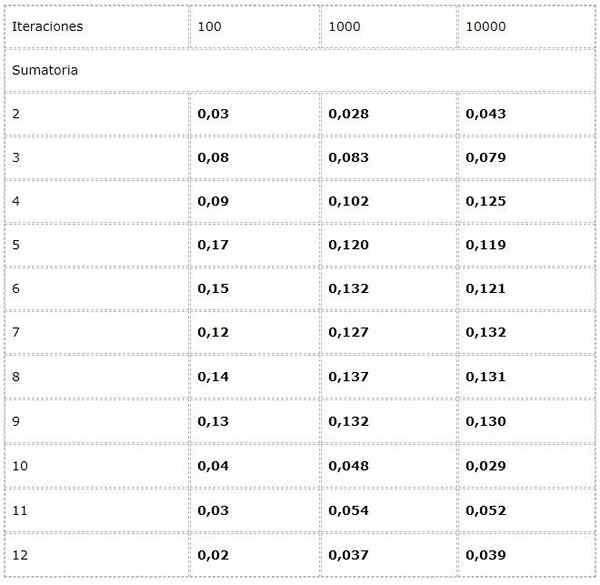
Diperhatikan bahawa hasilnya mungkin berbeza -beza antara lelaran. Walau bagaimanapun, undang -undang bilangan besar dapat dilihat dalam penumpuan yang jelas yang dibentangkan dalam dua lajur terakhir.

Rujukan

1. Statistik dan penilaian bukti untuk saintis forensik. Edisi kedua. Colin G.G. Aitken. Sekolah Matematik. Universiti Edinburgh, UK
2. Matematik untuk Sains Komputer. Eric Lehman. Google Inc.
   F Thomson Leighton Jabatan Matematik dan Sains Komputer dan Makmal AI, Institut Teknologi Massachussetts; Akamai Technologies
3. Guru Aritmetik, Jilid 29. Majlis Kebangsaan Guru Matematik, 1981. Universiti Michigan.
4. Teori Pembelajaran dan Pengajaran Nombor: Penyelidikan dalam Kognisi dan Arahan / Disunting oleh Stephen R. Campbell dan Rina Zazkis. Ablex Publishing 88 Post Road West, Westport CT 06881
5. Bernoulli, j. (1987). Ars conjectandi- 4ème partie. Rouen: Irem.