Kaedah dan latihan pengaturcaraan bukan linear

The Pengaturcaraan bukan linear Ini adalah proses mengoptimumkan fungsi yang bergantung kepada beberapa pembolehubah bebas, yang seterusnya tertakluk kepada sekatan.

Sekiranya satu atau lebih sekatan, atau jika fungsi untuk memaksimumkan atau meminimumkan (dipanggil Fungsi objektif), tidak dinyatakan sebagai gabungan linear pembolehubah, jadi ada masalah pengaturcaraan bukan linear.

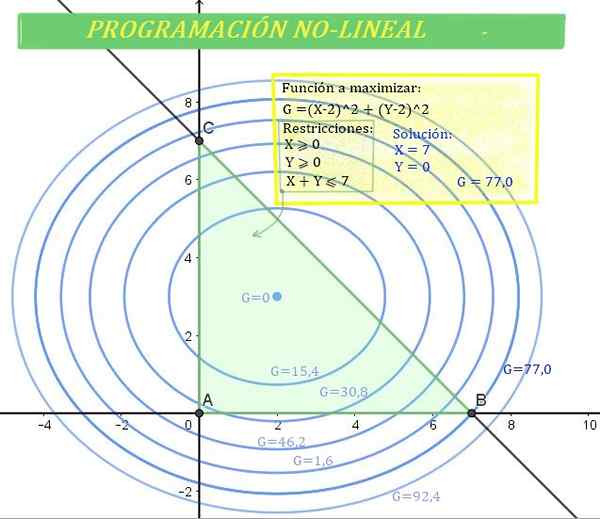
Rajah 1. Masalah pengaturcaraan bukan linear (NLP). di mana g ialah fungsi (tidak linear) untuk mengoptimumkan di rantau hijau, ditentukan oleh sekatan. Sumber: f. Zapata.

Dan oleh itu prosedur dan kaedah pengaturcaraan linear tidak dapat digunakan.

Contohnya, kaedah yang terkenal tidak dapat digunakan Simplex, yang hanya terpakai apabila fungsi objektif dan sekatan adalah gabungan linear dari pembolehubah masalah.

[TOC]

Kaedah pengaturcaraan linear

Untuk pengaturcaraan bukan linear kaedah utama yang akan digunakan ialah: 

1.- Kaedah grafik.

2.- Lagrange Multipliers untuk meneroka sempadan kawasan penyelesaian.

3.- Pengiraan kecerunan untuk meneroka hujung fungsi objektif.

4.- Kaedah langkah menurun, untuk mencari titik kecerunan sifar.

5.- Kaedah Modified Lagrange Multipliers (dengan keadaan Karush-Kuhn-Tucker).

Contoh penyelesaian dengan kaedah grafik

Contoh penyelesaian dengan kaedah grafik adalah apa yang dapat dilihat dalam Rajah 2:

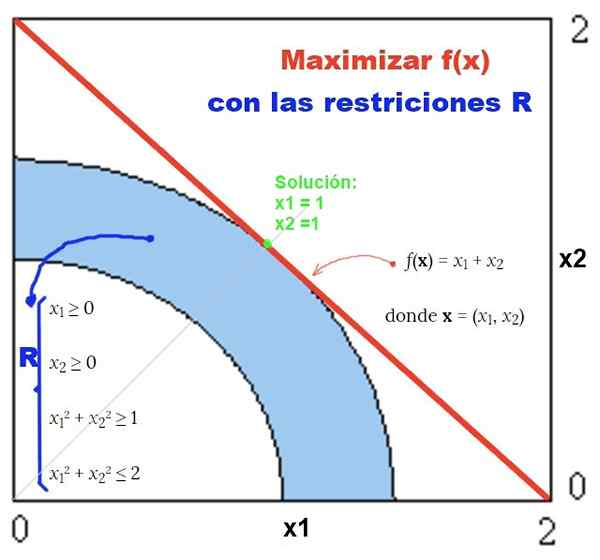Rajah 2. Contoh masalah bukan linear dengan sekatan bukan lineal dan penyelesaian grafiknya. Sumber: f. Zapata.

Latihan

- Latihan 1 (Kaedah Grafik)

Keuntungan g syarikat tertentu bergantung kepada jumlah yang dijual produk X dan jumlah yang dijual dari produk dan, sebagai tambahan keuntungan ditentukan oleh formula berikut:

Boleh melayani anda: Binomial konjugasi: Bagaimana ia diselesaikan, contoh, latihan

G = 2 (x - 2)² + 3 (dan - 3)²

Telah diketahui bahawa jumlah x dan y mempunyai sekatan berikut:

X≥0; Y≥0 dan x + dan ≤ 7

Tentukan nilai x dan y yang menghasilkan keuntungan maksimum.

Rajah 3. Keuntungan syarikat boleh dimodelkan secara matematik untuk mencari keuntungan maksimum oleh pengaturcaraan bukan linear. Sumber: Pixabay.

Penyelesaian 

Dalam masalah ini fungsi objektif bukan linear, sementara ketidaksamaan yang menentukan sekatan adalah. Ia adalah masalah Pengaturcaraan bukan linear.

Untuk penyelesaian masalah ini, kaedah grafik akan dipilih.

Pertama, rantau penyelesaian akan ditentukan, yang diberikan oleh sekatan.

Sebagai x≥0; Y≥0, penyelesaiannya perlu mencari dalam kuadran pertama satah XY, tetapi sebagai tambahan ia mesti dipenuhi bahawa x + y ≤ 7, penyelesaiannya berada di bawah semiplane garis x + y = 7.

Kawasan penyelesaian adalah persimpangan kuadran pertama dengan semiplane yang lebih rendah garis, yang menimbulkan ke rantau segi tiga di mana penyelesaiannya terletak. Sama seperti yang ditunjukkan dalam Rajah 1.

Sebaliknya, Gain G juga boleh diwakili dalam pesawat Cartesian, kerana persamaannya adalah elips dengan pusat (2,3).

Ellipse ditunjukkan dalam Rajah 1 untuk beberapa nilai g. Nilai g yang lebih tinggi, keuntungan yang lebih besar.

Terdapat penyelesaian yang dimiliki oleh rantau ini, tetapi tidak memberikan nilai maksimum g, sementara yang lain, seperti g = 92.4, keluar dari zon hijau, iaitu zon penyelesaian.

Kemudian, nilai maksimum g, seperti yang dimiliki oleh rantau penyelesaian sepadan dengan: 

Boleh melayani anda: kebarangkalian teoritis: bagaimana untuk mengeluarkannya, contoh, latihan

G = 77 (keuntungan maksimum), yang berlaku untuk x = 7 e y = 0. 

Menariknya, keuntungan maksimum berlaku apabila jumlah jualan produk dan tidak sah, sementara jumlah produk X mencapai nilai yang paling mungkin.

- Latihan 2 (Kaedah Analisis: Pengganda LaGrange) 

Cari penyelesaian (x, y) yang menjadikan fungsi f (x, y) = x² + 2 dan² maksimum di rantau g (x, y) = x² + dan² - 1 = 0.

Penyelesaian

Ia jelas merupakan masalah pengaturcaraan bukan linear, kerana kedua-dua fungsi objektif f (x, y) dan sekatan g (x, y) = 0, bukan gabungan linear pembolehubah x dan y.

Kaedah pengganda LaGrange akan digunakan, yang pertama kali memerlukan fungsi LaGrange L (x, y, λ):

L (x, y, λ) = f (x, y) - λ g (x, y) = x² + 2 dan² - λ (x² + dan² - 1) 

Di mana λ adalah parameter yang dipanggil Lagrange Multiplier.

Untuk menentukan nilai ekstrem fungsi objektif f, di rantau penyelesaian yang diberikan oleh sekatan g (x, y) = 0, langkah -langkah ini diikuti:

-Cari derivatif separa fungsi LaGrange L, berkenaan dengan x, y, λ.

-Sifar setiap derivatif.

Di sini urutan operasi ini:

1. ∂l/∂x = 2x - 2λx = 0
2. ∂l/∂y = 4y - 2λy = 0
3. ∂l/∂λ = -(x² + dan² - 1) = 0

Penyelesaian sistem yang mungkin

Penyelesaian kemungkinan sistem ini adalah λ = 1 untuk memenuhi persamaan pertama, di mana kes y = 0 untuk memenuhi yang kedua.

Penyelesaian ini menunjukkan bahawa x = 1 atau x = -1 supaya persamaan ketiga berpuas hati. Dengan cara ini dua penyelesaian S1 dan S2 telah diperolehi:

S1: (x = 1, y = 0)

S2: (x = -1, y = 0).

Alternatif lain ialah λ = 2 untuk persamaan kedua untuk dipenuhi, tanpa mengira nilai dan.

Ia dapat melayani anda: had fermat: apa yang terdiri dan latihan diselesaikan

Dalam kes ini, satu -satunya cara untuk persamaan pertama dipenuhi ialah x = 0. Memandangkan persamaan ketiga, terdapat hanya dua penyelesaian yang mungkin, yang akan kita panggil S3 dan S4:

S3: (x = 0, y = 1)

S4: (x = 0, y = -1)

Untuk mengetahui mana atau mana dari penyelesaian ini memaksimumkan fungsi objektif, teruskan untuk menggantikan f (x, y):

S1: f (1, 0) = 1² + 2.0² = 1

S2: f (-1, 0) = (-1)² + 2.0² = 1

S3: F (0, 1) = 0² + 2.1² = 2

S4: F (0, -1) = 0² + dua puluh satu)² = 2

Kami menyimpulkan bahawa penyelesaian yang memaksimumkan f, apabila x dan y tergolong dalam lilitan g (x, y) = 0 adalah s3 dan s4.

Pasangan nilai (x = 0, y = 1) y (x = 0, y = -1) memaksimumkan f (x, y) di rantau penyelesaian g (x, y) = 0.

- Latihan 3 (Gradien Null)

Cari penyelesaian (x, y) untuk fungsi objektif:

f (x, y) = x² + 2 dan²

Maksimum di rantau g (x, y) = x² + dan² - 1 ≤ 0.

Penyelesaian

Latihan ini adalah serupa dengan Latihan 2, tetapi rantau penyelesaian (atau sekatan) meluas ke kawasan dalaman lilitan G (x, y) = 0, iaitu bulatan g (x, y) ≤ 0. Ini termasuk lilitan dan kawasan dalamannya.

Penyelesaian sempadan telah ditentukan dalam Latihan 2, tetapi perlu meneroka kawasan dalaman.

Untuk melakukan ini, kecerunan fungsi f (x, y) mesti dikira dan sama dengan sifar, untuk mencari nilai yang melampau di rantau penyelesaian. Ini bersamaan dengan mengira derivatif separa f berkenaan dengan x dan masing -masing dan menyamakan sifar:

∂f/∂x = 2 x = 0

∂f/∂y = 4 y = 0

Sistem persamaan ini mempunyai satu -satunya penyelesaian (x = 0, y = 0) yang dimiliki oleh bulatan g (x, y) ≤ 0.

Menggantikan nilai ini dalam fungsi F hasil:

f (0, 0) = 0

Kesimpulannya, nilai maksimum yang mengambil fungsi di rantau penyelesaian adalah 2 dan berlaku di sempadan rantau penyelesaian, untuk nilai (x = 0, y = 1) y (x = 0, y = -1).

 Rujukan

1. Avriel, m. 2003. Pemrograman tak linear. Penerbitan Dover.
2. Bazaraa. 1979. Pemrograman tak linear. John Wiley & Sons.
3. Bertsekas, d. 1999. Pemrograman bukan linear: Edisi ke -2. Athena Scientific.
4. Nocedal, J. 1999. Pengoptimuman berangka. Springer-Verlag.
5. Wikipedia. Pengaturcaraan bukan linear. Pulih dari: Adakah.Wikipedia.com