Matematik

Sifat radikal

1014
72
Kerry Schmitt

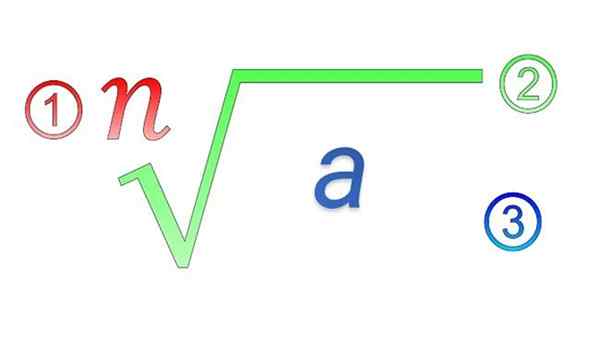
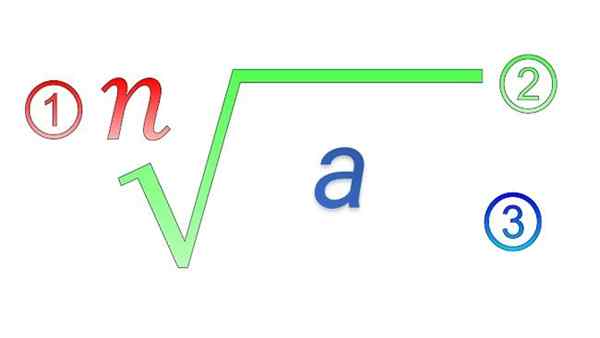Unsur radikal: 1) indeks; 2) simbol radikal; 3) Kuantiti subradikal

Apakah sifat radikal?

The sifat radikal Mereka adalah operasi yang membolehkan menyelesaikan masalah radikal dan kuasa yang kompleks. Radikal adalah cara untuk melambangkan matematik ke n-eme jumlah "a". Akar ini adalah jumlah lain, yang dipanggil "B", sehingga namanya tepat "A", jadi sah untuk menulis yang berikut:

$\dpi110 \sqrt[n]a=b\Rightarrow b^n=a$

Nilai "n" adalah nombor semula jadi, yang dikenali sebagai indeks akar, "a" adalah Radikan atau kuantiti subradikal, dan "b" adalah n-eme dari "a" akar. Kedua -dua "A" dan "B" tergolong dalam set nombor sebenar.

Sekiranya indeks tidak ditulis dalam radikal, ia difahami dengan segera bahawa nilainya adalah sama dengan 2 dan berbunyi "akar persegi a".

Oleh kerana "n" tergolong dalam set nombor semula jadi, ia boleh menjadi pasangan atau nombor ganjil. Kemudian, kes -kes berikut dibezakan:

Untuk "n" par

Sekiranya> 0 atau sama dengan 0, akar n-alkal "a" positif atau 0, dan dipanggil akar utama.
Bila hendak < 0, no existe raíz n-ésima en el conjunto de los números reales, pero sí en los números complejos.

Untuk "n" ganjil

Ya a> 0, n-eme akar "a" positif.
Bila hendak< 0, la raíz n-ésima de “a” es negativa.

Beberapa contoh adalah seperti berikut:

$\dpi110 \sqrt49=7\Rightarrow 7^2=49$

$\dpi110 \sqrt[3]\left ( -729 \right )=-9\Rightarrow \left ( -9 \right )^3=-729$

$\dpi110 \sqrt3=1.7320508…$

Sifat penggambaran

Adalah mungkin untuk menulis nama jumlah jumlah sebagai kuasa dengan eksponen pecahan, iaitu nombor rasional.

Dalam kes ini, indeks root menjadi penyebut, manakala eksponen jumlah subradikal menjadi pengangka:

Boleh melayani anda: Fungsi homografi: Cara graf, latihan yang diselesaikan

$\dpi110 \sqrt[n]a^m=a^\fracmn$

Ungkapan yang sah selagi n ≠ 0, kerana tiada pecahan dengan penyebut dimasukkan.

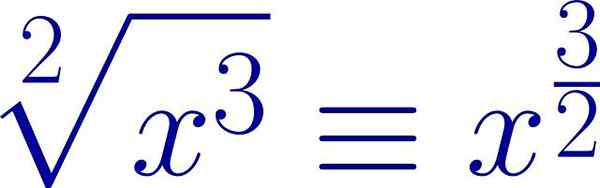Contoh ungkapan radikal yang ditulis dalam bentuk eksponen pecahan. Indeks root adalah penyebut eksponen, sementara kuasa siaran adalah pengangka. Sumber: Wikimedia Commons.

Dengan cara ini, sifat yang sama yang digunakan untuk kuasa, boleh digunakan dalam hal radikal.

Untuk nilai yang dimiliki oleh set nombor sebenar, sifat -sifat ini adalah seperti berikut:

1. Produk radikal indeks yang sama

Dalam produk dua (atau lebih) radikal indeks yang sama, jumlah subradikal didarabkan, mengekalkan indeks:

$\dpi110 \sqrt[n]a\cdot \sqrt[n]b=\sqrt[n]a\cdot b$

2. Radikal quotient indeks yang sama

Kota antara akar N-"A" dan N-Eme "B", yang B ≠ 0, adalah sama dengan akar N-emeasy dari quotient antara "A" dan "B":

$\dpi110 \frac\sqrt[n]a\sqrt[n]b=\sqrt[n]\fracab$

3. Akar akar

Untuk mencari akar n-emeasy dari m-eme jumlah "a", jumlah subradikal ditulis di bawah akar yang indeksnya adalah produk antara "n" dan "m":

$\dpi110 \sqrt[n]\sqrt[m]a=\sqrt[n\cdot m]a$

Prosedur ini mudah dilanjutkan ke akar bersarang berturut -turut. Indeks akar yang dihasilkan adalah produk semua indeks, seperti ini:

$\dpi110 \sqrt[n]\sqrt[m]\sqrt[p]\sqrt[q]a=\sqrt[n\cdot m\cdot p\cdot q]a$

4. Kuasa akar

A n-yang dibangkitkan kepada kuasa m, menyatakan jumlah subradikal kepada kuasa tersebut:

$\dpi110 \left ( \sqrt[n]a \right )^m=\sqrt[n]a^m=a^\fracmn$

Kes tertentu:

1) Ya n = m, Tanda akar hilang, meninggalkan pangkalan ditinggikan ke kuasa 1:

$\dpi110 \left ( \sqrt[n]a \right )^n=\sqrt[n]a^n=a$

Yang sah untuk ≥ 0. Secara umum, jika indeks root adalah nombor juga, anda mempunyai:

$\dpi110 \left ( \sqrt[n]a \right )^n=\left| a\right|$

(Lihat contoh kemudian)

2) Ya m> n, Pecahan m/n tidak wajar dan akar dapat dipermudahkan, sebagai contoh, mencari pecahan yang setara dengan m/n supaya pengangka dan penyebut sepupu antara satu sama lain, atau menulis semula jumlah subradical dan memohon beberapa Hartanah yang diterangkan di sini.

Boleh melayani anda: prisma dan piramid

(Lihat contoh kemudian)

5. Penguatan radikal

Radikal dapat dikuatkan dengan faktor q, Jika kedua -dua indeks root, serta kuasa kuantiti subradikal, darab dengan faktor tersebut, dan operasi ini tidak melibatkan pengubahsuaian hasilnya. Oleh itu:

$\dpi110 \sqrt[n]a^m=\sqrt[n\cdot q]a^m\cdot q$

Dengan syarat bahawa ≥ 0 ketika ia berada.

6. Pengenalan faktor dalam radikal

Sekiranya faktor "b" positif mendarabkan radikal, ia boleh lulus di dalamnya, jika ia naik ke indeks akar yang sama. Kalau macam itu:

$\dpi110 b\sqrt[n]a^m=\sqrt[n]b^n\cdot a^m$

7. Jumlah dan penolakan radikal

Radikal boleh menambah dan tolak, selagi ia adalah indeks yang sama dan mempunyai jumlah subradikal yang sama.

Apabila dua atau lebih radikal adalah indeks yang sama dan kuantiti subradikal, dikatakan bahawa mereka adalah Radikal yang sama.

Sebagai contoh, radikal berikut adalah serupa:

$\dpi110 \sqrt[3]5,\: -7\sqrt[3]5,\: 10\sqrt[3]5$

Sebaliknya, radikal ini tidak sama, kerana mereka tidak mempunyai jumlah subradikal yang sama:

$\dpi110 \sqrt2,\: \sqrt3$

Kedua -dua ini sama:

$\dpi110 \sqrt7,\: \sqrt[4]7$

Oleh kerana indeks radikal tidak sama.

Radikal yang sama dapat dikurangkan kepada satu, menambah atau menolak pekali yang menemani mereka.

Contoh sifat radikal

Contoh 1

Apakah nilai akar berikut?

$\dpi110 \sqrt32,\: \sqrt[3]-8,\: \sqrt[4]81,\: \sqrt-8$

Akar kuadrat 32 boleh didapati secara langsung dengan bantuan kalkulator. Nilainya ialah:

$\dpi110 \sqrt32=5.656854249…$

Titik yang menggalakkan menunjukkan bahawa terdapat perpuluhan yang tidak terhingga.

Jika anda lebih suka tidak bekerja dengan nombor perpuluhan, akar persegi 32 juga boleh dikira dengan menguraikan 32 dalam faktor utama:

32 = 2⁵

Dengan cara ini, apabila menggantikannya, ia diperolehi:

Boleh melayani anda: Pembahagi 8: Apa dan Penjelasan Mudah

$\dpi110 \sqrt32=\sqrt2^5$

Ditulis sebagai eksponen pecahan:

$\dpi110 \sqrt32=\sqrt2^5=2^\frac52$

Pecahan 5/2 adalah tidak wajar, jadi radikal dapat dipermudahkan, menggunakan sifat -sifat kuasa:

$\dpi110 \sqrt32=\sqrt2^5=\sqrt2\cdot 2^4$

Sekarang memohon harta 1 di atas:

$\dpi110 \sqrt2\cdot 2^4=\sqrt2\cdot \sqrt2^4=\sqrt2\cdot \sqrt16=4\sqrt2$

Oleh itu:

$\dpi110 \sqrt32=4\sqrt2$

Untuk bahagiannya:

$\dpi110 \sqrt[3]-8=-2$

Sejak (-2)³ = -8.

Menurut harta 4:

$\dpi110 \sqrt[4]81=\sqrt[4]3^4=3$

Dan akhirnya, akar kuadrat -8 tidak wujud dalam set nombor nyata, walaupun dalam bilangan kompleks.

Contoh 2

Memandangkan operasi berikut:

$\dpi110 4\sqrt8+\sqrt81-3\sqrt32$

Adakah mungkin untuk mengurangkan hasilnya?

Dengan syarat bahawa radikal adalah serupa, adalah mungkin untuk mengurangkannya, tetapi untuk ini mereka mesti mempunyai indeks yang sama dan kuantiti subradikal yang sama. Dalam contoh sebelumnya ia dilihat bahawa:

$\dpi110 \sqrt32=4\sqrt2$

Prosedur analog boleh digunakan untuk menulis penambahan pertama, supaya jumlah subradikal adalah sama dengan 2:

$\dpi110 4\sqrt8=4\sqrt2^3=4\sqrt2^2\cdot 2=4\sqrt2^2\cdot \sqrt2=4\cdot 2\cdot\sqrt2=8\sqrt2$

Radikal ini serupa dengan sebelumnya. Bagi akar kuadrat 81, ini adalah 9, oleh itu:

$\dpi110 4\sqrt8+\sqrt81-3\sqrt32=8\sqrt2+9-3\cdot 4\sqrt2=8\sqrt2+9-12\sqrt2=(8-12)\sqrt2+9=-4\sqrt2+9$

Contoh 3

Apa sifat yang diperlukan untuk melaksanakan operasi ini?

$\dpi110 \sqrt[3]x\sqrtx$

Kita mesti memohon sifat 3 dan 5, masing -masing, akar akar dan pengenalan nilai radikal. Pertama, harta 5 terpakai, untuk memperkenalkan "x" yang berada di luar akar paling dalam:

$\dpi110 \sqrt[3]x\sqrtx=\sqrt[3]\sqrtx^2\cdot x=\sqrt[3]\sqrtx^3$

Dan sekarang ungkapan itu siap untuk memohon harta 3, dan melipatgandakan indeks masing -masing radikal:

$\dpi110 \sqrt[3]x\sqrtx=\sqrt[3]\sqrtx^2\cdot x=\sqrt[3]\sqrtx^3=\sqrt[6]x^3$

Rujukan

Gonzales, d. 2011. Algebra Asas: Teori dan Amalan. 2. Edisi.
Haeussler, e. 2012. Precalculation. 1st. Edisi. Pearson.
Khan Aistaem. Eksponen dan radikal. Pulih dari: Khanacademy.org.
Larson, r. 2012. Precalculation. Ke -8. Edisi. Pembelajaran Cengage.
Stewart, J. 2007. Matematik untuk pengiraan. 5th. Edisi. Pembelajaran Cengage.