Apakah momen magnet?

Dia Momen magnet Ia adalah vektor yang mengaitkan arus yang melintasi sedikit atau gelung tertutup dengan kawasan yang sama. Modulnya sama dengan produk intensiti arus oleh kawasan, dan arah dan arahnya diberikan oleh peraturan tangan kanan, seperti yang ditunjukkan dalam Rajah 1.

Definisi ini sah tanpa mengira. Bagi perpaduan momen magnet, dalam sistem unit antarabangsa jika ia adalah ampere × m².

Rajah 1. Vektor momen magnet dari ikatan semasa sewenang -wenangnya berserenjang dengan satahnya dan arahnya ditentukan oleh peraturan ibu jari kanan. Sumber: Wikimedia Commons.

Dalam istilah matematik, menandakan momen magnet vektor dengan lirik Yunani μ (Dengan berani kerana ia adalah vektor dan dengan itu membezakan dirinya dari magnitudnya), ia dinyatakan sebagai:

μ = IA n

Di mana saya adalah intensiti arus, a adalah kawasan yang melampirkan gelung dan n Ia adalah vektor unit (modul yang sama dengan 1) yang menunjukkan arah yang berserenjang dengan satah spase, dan makna yang diberikan oleh peraturan ibu jari kanan (lihat Rajah 1).

Peraturan ini sangat mudah: menggulung empat jari tangan kanan sehingga mereka mengikuti arus, ibu jari menunjukkan arah dan arah n dan oleh itu momen magnet.

Persamaan sebelumnya sah untuk gelung. Sekiranya terdapat nougas seperti dalam gegelung, momen magnetik didarab dengan n:

μ = nIA n

[TOC]

Momen magnet dan medan magnet

Sangat mudah untuk mencari ungkapan untuk momen magnet giliran dengan bentuk geometri biasa:

-Sisi persegi sisi ℓ: μ = Iℓ² n

-Sisi spiral segi empat tepat ke dan b: μ = IAB n

-Radio R. Radio Spira: μ = Iπr² n

Boleh melayani anda: nombor atom

Medan magnet Dipolo

Medan magnet yang dihasilkan oleh gelung atau spase semasa menyerupai magnet bar dan juga bumi.

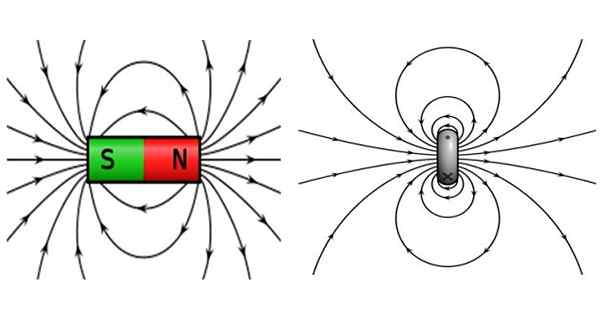Rajah 2. Di sebelah kiri medan magnet magnet bar dan ke kanan yang menghasilkan lingkaran bulat yang mengangkut arus. Sumber: Wikimedia Commons.

Magnet bar dicirikan dengan mempunyai tiang utara dan tiang selatan, di mana tiang bertentangan tertarik dan tiang yang sama menangkis. Garis medan ditutup, biarkan tiang utara dan sampai ke tiang selatan.

Sekarang, tiang magnet tidak dapat dipisahkan, yang bermaksud bahawa jika magnet bar dibahagikan kepada dua magnet yang lebih kecil, mereka terus memiliki tiang utara dan selatan mereka sendiri. Tidak mungkin mempunyai tiang magnet terpencil, sebab itulah magnet bar dipanggil Dipolo magnet.

Medan magnet radius r spiral r, yang mengangkut arus i, dikira oleh undang-undang biot-savart. Untuk mata yang dimiliki oleh paksi simetri (dalam kes ini paksi x), medan diberikan oleh:

Di mana μ_{Sama ada} Ia adalah kebolehtelapan vakum. Mengambil medan di titik jauh dari spase, yang mana ia dipenuhi bahawa x >> r, lapangan mendekati:

Hubungan antara medan magnet dan momen magnet dipolo

Termasuk momen magnet dalam ungkapan sebelumnya ialah:

Dengan cara ini, intensiti medan magnet adalah berkadar dengan momen magnet. Perhatikan bahawa intensiti medan berkurangan dengan kiub jarak.

Pendekatan ini boleh digunakan untuk mana -mana gelung, selagi x besar berbanding dengan dimensinya.

Dan sebagai garis bidang ini menyerupai magnet bar, persamaan adalah model yang baik untuk medan magnet ini dan sistem lain yang garisnya sama, seperti: sebagai contoh:

Boleh melayani anda: penyerapan: apakah, contoh dan latihan diselesaikan

-Zarah dimuatkan dalam gerakan sebagai elektron.

-Atom.

-Bumi dan planet dan satelit lain sistem solar.

-Bintang.

Kesan medan luaran pada gelung

Ciri yang sangat penting dalam momen magnet adalah pautannya kepada tork bahawa pengalaman gelung di hadapan medan magnet luaran.

Motor elektrik mengandungi gegelung di mana aliran arah berubah berjalan dan terima kasih kepada bidang luaran yang mengalami kesan giliran. Giliran ini menjadikan paksi bergerak dan tenaga elektrik menjadi tenaga mekanikal semasa proses.

Tork pada gelung segi empat tepat

Katakan, untuk memudahkan pengiraan, sisi segi empat tepat ke dan b, yang vektor biasa n, skrin keluar, pada mulanya ia berserenjang dengan medan magnet seragam B, Seperti dalam Rajah 3. Sisi pengalaman pengalaman gelung yang diberikan oleh:

F = IL x B

Di mana L Ia adalah vektor magnitud yang sama dengan panjang segmen dan diarahkan mengikut arus, dan intensiti yang sama dan B Ia adalah bidang. Kekuatan berserenjang dengan kedua -duanya L Seperti bidang, tetapi tidak semua pihak mengalami kekuatan.

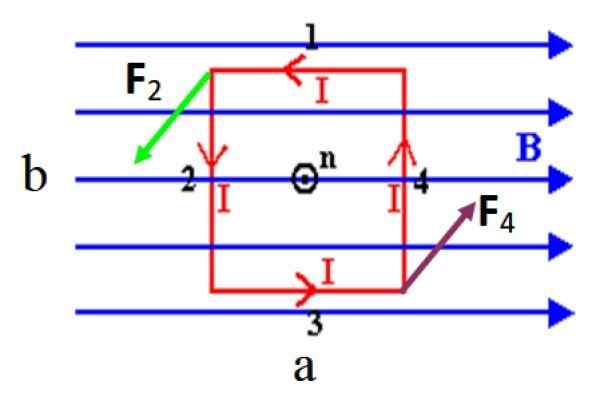Rajah 3. Lingkaran segi empat tepat yang mengangkut arus saya dalam erti kata anti -horary, mengalami tork dengan kehadiran medan magnet seragam seragam. Sumber: f. Zapata.

Dalam angka yang ditunjukkan, tidak ada kekuatan pada sisi pendek 1 dan 3 kerana selari dengan medan, ingat bahawa produk silang antara vektor selari adalah tidak sah. Walau bagaimanapun, sisi panjang 2 dan 4, yang tegak lurus B, mereka mengalami kekuatan yang ditandakan sebagai F₂ dan F₄.

Bentuk kuasa ini sepasang: Mereka mempunyai magnitud dan arah yang sama, tetapi deria yang bertentangan, oleh itu mereka tidak dapat bergerak ke gelung di tengah -tengah bidang. Tetapi mereka boleh membuatnya berputar, kerana tork  τ Bahawa setiap daya dikenakan, berkenaan dengan paksi menegak yang melewati pusat gelung, ia mempunyai arah dan makna yang sama.

Boleh melayani anda: daya perpaduan

Menurut definisi tork, di mana r Ia adalah vektor kedudukan:

τ = r x F

Jadi:

τ₂ = τ₄=(A/2) f (+J )

Tork individu tidak dibatalkan, kerana mereka mempunyai arah dan makna yang sama, maka mereka ditambah:

τ_jaring = τ₂ + τ₄ = a f (+J )

Dan menjadi magnitud daya F = IBB, ia hasil:

τ_jaring = I ⋅ a ⋅B ⋅B (+J )

Produk a ⋅B adalah kawasan A dari spase, jadi IAB adalah magnitud momen magnet μ. Oleh itu τ_jaring = μ ⋅B (+J )

Dapat dilihat bahawa, secara umum, tork bertepatan dengan produk vektor antara vektor μ dan B:

τ_jaring = μ x B

Dan walaupun ungkapan ini diperoleh dari gelung segi empat tepat, ia sah untuk pijakan rata sewenang -wenangnya.

Kesan medan pada gelung adalah tork yang cenderung menyelaraskan momen magnet dengan medan.

Tenaga berpotensi dipole magnet

Untuk menghidupkan lingkaran atau dipole di tengah -tengah padang, kerja mesti dilakukan terhadap daya magnet, yang mengubah potensi tenaga dipolo. Variasi tenaga ΔU, apabila lingkaran berputar dari sudut θ_{Sama ada} Pada sudut θ diberikan oleh integral:

Sekiranya tahap rujukan dipilih sebagai θ_{Sama ada} = π/2:

Δu = -μb cos θ

Yang seterusnya dapat dinyatakan sebagai produk skalar antara vektor B dan μ:

ΔU = - μ ·B

Tenaga berpotensi minimum di dipole berlaku apabila cos θ = 1, yang bermaksud bahawa μ dan B Mereka selari, tenaga adalah maksimum jika ia bertentangan (θ = π) dan null apabila mereka berserenjang (θ = π/2).

Rujukan

1. Figueroa, d. 2005. Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 5. Elektromagnetisme. Diedit oleh Douglas Figueroa (USB).
2. Resnick, r. 1999. Fizikal. Vol. 2. Edisi ke -3. dalam bahasa Sepanyol. Syarikat Editorial Continental s.Ke. daripada c.V.
3. Sears, Zemansky. 2016. Fizik universiti dengan fizik moden. Ke -14. Ed. Jilid 2. Pearson.
4. Serway, r., Jewett, J. (2008). Fizik untuk Sains dan Kejuruteraan. Jilid 2. Ke -7. Ed. Pembelajaran Cengage.
5. Tipler, ms. (2006) Fizik untuk Sains dan Teknologi. Edisi ke -5. Jilid 2. Editorial kembali.