Apakah panduannya? (Geometri)

The arahan Dalam geometri ia terdiri daripada lengkung, permukaan atau kelantangan yang tetap tetap dan menentukan cara di mana objek geometri terbentuk. Contohnya, dengan garis lengkung lain seperti permukaan kerucut, dan revolusi, seperti silinder bulat lurus ditubuhkan.

Lengkung garis panduan juga boleh menjadi lilitan. Silinder bulat lurus boleh dibentuk dengan meninggalkan radius ri -r rión ri.

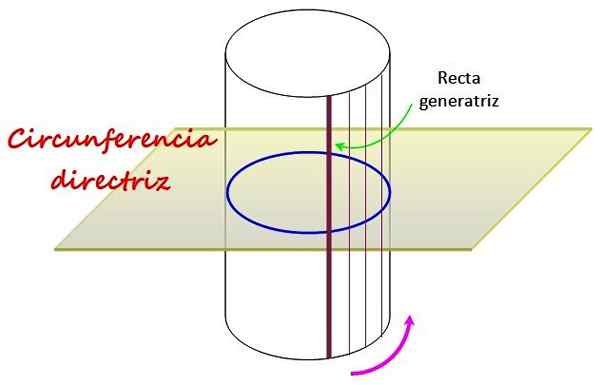
Rajah 1. Silinder bulat lurus mempunyai sebagai panduan bulatan, di mana garis lurus yang dipanggil Generatrix bergerak. Sumber: f. Zapata.

Lingkaran, yang berada di atas satah yang ditarik dalam angka itu, menentukan bentuk permukaan melengkung silinder pekeliling lurus, yang dihasilkan oleh berputar di sekelilingnya, yang dipanggil Generatrix lurus.

Sekiranya lengkung bimbingan bukan lilitan, tetapi lengkung lain, jenis silinder lain dihasilkan, seperti silinder elips, yang garis panduannya adalah elips.

Lilitan juga boleh bertindak sebagai garis panduan untuk menjana lengkung lain, seperti halnya Epitrocoid, Keluk dalam satah yang dihasilkan oleh satu titik, yang seterusnya berada dalam lingkaran yang lebih kecil yang menggulung tanpa gelongsor, di sekitar garis panduan.

Lebih mudah untuk menghargainya secara visual dengan animasi berikut:

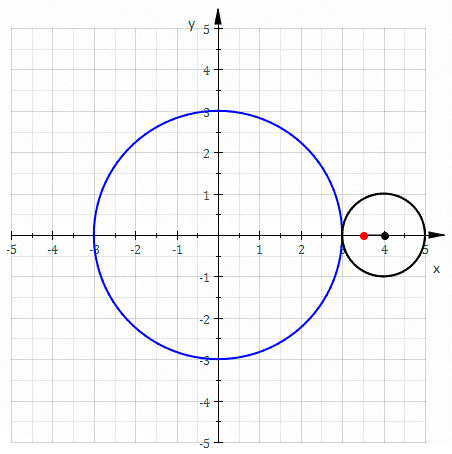Rajah 2. Lengkung merah dipanggil Epitrocide dan lengkung garis panduannya. Sumber: Wikimedia Commons. Sam Derbyshire di Wikipedia Inggeris/CC BY-S (http: // creativeCommons.Org/lesen/by-sa/3.0/).

Lengkung garis panduan pada permukaan silinder

Permukaan silinder diklasifikasikan mengikut lengkung garis panduan mereka dalam silinder:

-Bulat

-Elips

-Parabola

-Hiperbolik

Apabila permukaan silinder mempunyai garis panduan yang terletak pada satah yang berserenjang dengan garis Generatrix, persamaan permukaan tersebut adalah sama dengan garis panduan garis panduan.

Ia dapat melayani anda: apakah hubungan antara kawasan rhombus dan segi empat tepat?

Silinder tergolong dalam kumpulan Permukaan quadric, Persamaannya adalah gred kedua dengan tiga pembolehubah. Bentuk umum ialah:

Kapak² + Oleh² + Cz² + DXY + EXZ + FYZ + GX + HY + IZ + K = 0

Di mana koefisien a, b, c ... adalah nombor sebenar.

Silinder adalah badan geometri tiga dimensi yang paling biasa dan berguna yang dapat dijumpai, terutama silinder bulat lurus, tetapi jenis silinder lain yang diterangkan di bawah juga mempunyai aplikasi dalam kejuruteraan dan reka bentuk.

Silinder pekeliling lurus

Garis panduannya adalah bulatan C yang berada dalam satah serenjang dengan silinder, seperti yang ditunjukkan dalam Rajah 1, kerana garis Generatrix, yang berjalan ke C untuk membentuk permukaan sisi, berserenjang dengan C C.

Persamaan lilitan C pada satah XY, memberi tumpuan kepada asal (0.0) adalah:

x² + dan² = R²

Di mana r, jejari lilitan jelas akan menjadi radius silinder. Ketinggian h silinder meluas di sepanjang paksi z, tegak lurus ke satah xy.

Silinder elips

Garis panduan ini adalah elips dalam pesawat XY yang berpusat pada asal (0.0), yang persamaannya adalah:

Generatrix adalah garis tegak lurus ke satah XY, yang bergerak di sekitar elips untuk menimbulkan permukaan sisi. Ellipse boleh berada di mana -mana ketinggian z pada pesawat xy.

Sebagai contoh, persamaan elips:

4x² + 9y² = 36

Ia adalah lengkung garis panduan yang menimbulkan silinder elips yang persamaannya adalah 4x² + 9y² = 36, ditambah z = 0. Menambah ungkapan terakhir ini, jelas bahawa ia adalah permukaan.

Boleh melayani anda: ralat pensampelan: formula dan persamaan, pengiraan, contoh

Silinder parabola

Dalam kes ini, garis panduan adalah perumpamaan, yang boleh menjadi bentuk y = x². Oleh itu, silinder diarahkan di sepanjang paksi z dan bentuk perumpamaan menyusun dengan puncak dalam (0.0) di sepanjang paksi itu.

Silinder parabola mempunyai aplikasi dalam tenaga solar, kerana beberapa pengumpul mempunyai cermin dengan cara itu, di mana cahaya matahari tertumpu dalam fokus. Titik ini melepasi paip lurus di mana minyak mencapai suhu sehingga 400 º c.

Silinder hiperbolik

Dalam silinder hiperbolik, persamaan garis panduan adalah hiperbola yang berpusat pada asalnya:

Silinder terbentuk pada timbunan.

Permukaan revolusi

Lengkung garis panduan permukaan revolusi adalah paksi revolusi yang sama, garis di mana lengkung yang bertanggungjawab menjana permukaan.

Keluk yang berkisar boleh mempunyai bentuk sewenang -wenang, dengan cara ini kawasan dijana seperti yang dilihat dalam animasi ini:

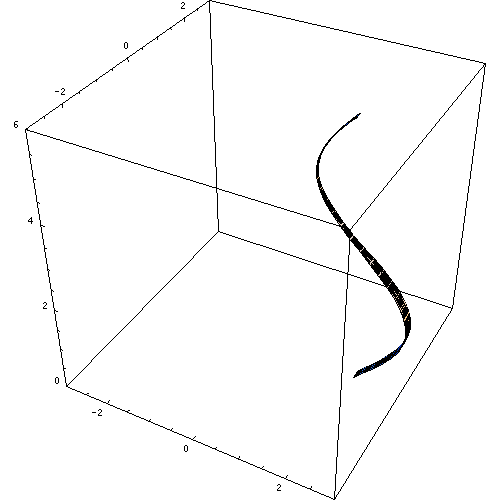Rajah 3. Permukaan revolusi. Sumber: Wikimedia Commons. https: // muat naik.Wikimedia.Org/wikipedia/commons/e/e7/rotationskoerper_animation.Gif.

Sekiranya garis lain dihidupkan garis panduan, silinder bulat lurus yang sudah biasa diperoleh. Dengan cara yang sama, permukaan revolusi lain boleh diperolehi, seperti permukaan revolusi kerucut, sfera dan toroidal.

Permukaan kerucut

Permukaan kerucut dihasilkan oleh pergerakan garis Generatrix yang selalu melalui lengkung rata atau lengkung garis panduan tetap dan dengan titik tetap yang dipanggil puncak, yang tidak tergolong dalam satah garis panduan.

Boleh melayani anda: Harapan Matematik: Formula, Hartanah, Contoh, Latihan

Puncak atau hujung membahagikan kon ke dalam dua bahagian, yang dipanggil daun Sama ada cawangan.

Latihan yang diselesaikan

- Latihan 1

Cari kawasan sisi silinder pekeliling tinggi ketinggian 25 cm, keluk garis panduannya adalah lilitan radius 6 cm, yang difokuskan pada asal.

Penyelesaian

Kawasan sisi silinder adalah hasil panjang garis panduan mengikut ketinggian. Jika R adalah jejari lilitan dan h ialah ketinggian silinder, kawasan diberikan oleh:

A = 2πr x H = 2πx 6 cm x 25 cm = 942.5 cm²

- Latihan 2

Anda mempunyai persamaan berikut yang sepadan dengan permukaan kuadrik:

x² + dan² + 2Z² +2xz - 2yz = 1

Nyatakan permukaannya dan apakah persamaan garis panduan.

Penyelesaian

Melakukan z = k, di mana k adalah malar, ia diperolehi:

x² + dan² + 2k² +2kx - 2ky = 1

Kami menyusun semula istilah seperti berikut:

(x² + 2kx) + (dan²- 2ky) = 1-2k²

Kuadrat mesti², Agar tidak mengubah mana -mana tanda kurung:

(x² + 2kx + k² - k² ) + (dan² - 2ky + k² - k²) = 1-2k²

(x² + 2kx + k²) - k²  + (dan²- 2ky + k²) - k² = 1-2k²

Dengan cara ini ia tetap:

(x + k)² + (dan - k)² = 1

Seperti persamaan bulatan tengah (-k, k) dan radius 1, permukaannya adalah silinder bulat lurus, juga radio 1, selagi garis generatrix berserenjang dengan lilitan tersebut.

Sebagai contoh, melakukan k = 0, persamaan dikurangkan ke lilitan yang berpusat pada asal (0.0) yang jejari adalah 1:

x² + dan² = 1

Rujukan

1. Gaussians. Mewakili permukaan tiga dimensi. Pulih dari: Gaussians.com.
2. Kindle, j. Teori dan masalah geometri analisis. McGraw Hill. Siri Schaum.
3. Permukaan sebagai tempat geometri. Pulih dari: algebra.FRLP.Utn.Edu.ar.
4. Suárez, m. Permukaan. Diperolehi dari: Subjek.Unq.Edu.ar.
5. Permukaan quadric. Pulih dari: sistem.fciencias.Unam.mx.