Apakah kelajuan linear? (Dengan latihan yang diselesaikan)

The Kelajuan linear Ia ditakrifkan sebagai apa yang selalu tangen dengan trajektori diikuti oleh zarah, tanpa mengira. Sekiranya zarah selalu bergerak dalam trajektori rectilinear, tidak ada masalah membayangkan bagaimana vektor halaju mengiringi garis lurus ini.

Walau bagaimanapun, secara umum pergerakan itu dijalankan pada lengkung sewenang -wenangnya. Setiap bahagian lengkung boleh dimodelkan seolah -olah ia adalah sebahagian daripada bulatan radio ke, yang pada setiap titik adalah tangen ke jalan yang diikuti.

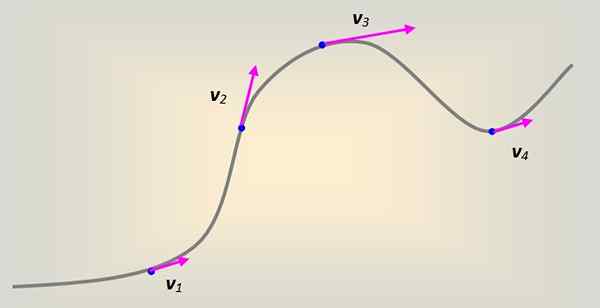
Rajah 1. Kelajuan linear pada telefon bimbit yang menggambarkan trajektori curvilinear. Sumber: Diri Diri.

Dalam kes ini, kelajuan linear mengiringi secara tangen dan pada setiap masa ke lengkung pada setiap titik itu.

Kelajuan linear segera secara matematik adalah terbitan kedudukan berkenaan dengan masa. Menjadi r vektor kedudukan zarah dalam sekejap t, Kemudian kelajuan linear diberikan oleh ungkapan:

v = r'(T) = dr / dt

Ini bermakna kelajuan linear atau kelajuan tangen, kerana ia juga dipanggil, tidak lain selain perubahan kedudukan berkenaan dengan masa.

[TOC]

Kelajuan linear dalam pergerakan bulat

Apabila pergerakan berada di lilitan, kita boleh pergi bersebelahan dengan zarah pada setiap titik dan melihat apa yang berlaku dalam dua arah yang sangat istimewa: salah seorang daripada mereka adalah yang selalu menunjuk ke pusat. Ini adalah alamat radial.

Arah penting lain adalah yang berlaku di lilitan, ini adalah alamat Tangential Dan kelajuan linear selalu memilikinya.

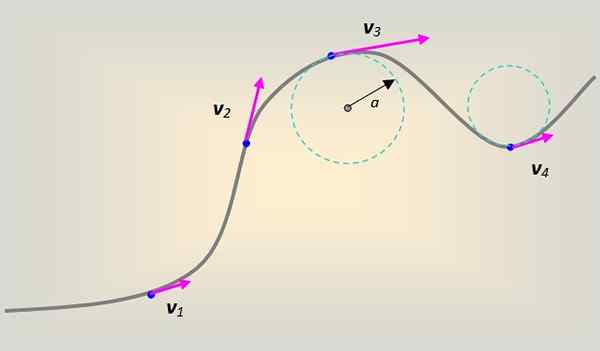
Boleh melayani anda: tekanan manometrik: penjelasan, formula, persamaan, contoh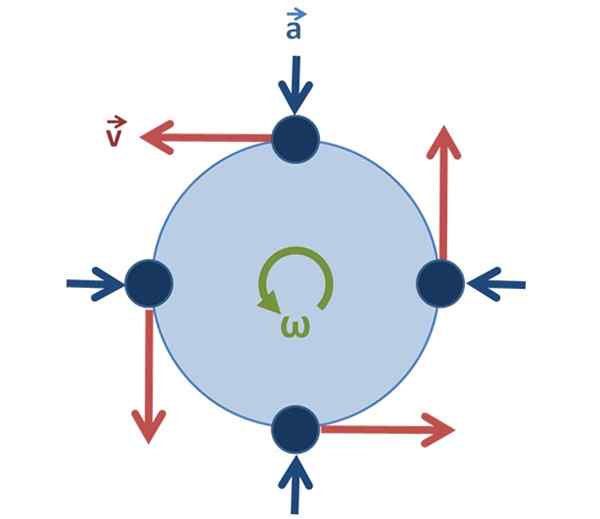Rajah 2. Pergerakan bulat seragam: vektor halaju mengubah arah dan arah apabila zarah berputar, tetapi magnitudnya sama. Sumber: Asal oleh Pengguna: Brews_OHARE, Svged oleh Pengguna: SJLEGG [CC BY-SA 3.0 (https: // creativeCommons.Org/lesen/by-sa/3.0)].

Sekiranya berlaku pergerakan pekeliling seragam, penting ya ia tetap tidak berubah.

Untuk pergerakan ini kedudukan sebagai fungsi masa diberikan oleh S (t), di mana s Adakah dia Tourd Arc dan t Sudah tiba masanya. Dalam hal ini, kelajuan seketika diberikan oleh ungkapan V = ds/dt Dan ia tetap.

Jika magnitud kelajuan juga berbeza -beza (kita sudah tahu bahawa arah selalu melakukannya, jika tidak, mudah alih tidak dapat berubah), kita menghadapi pergerakan bulat yang bervariasi, di mana mudah alih selain berputar, ia boleh berhenti atau mempercepatkan.

Kelajuan linear, halaju sudut dan pecutan sentripetal

Pergerakan zarah juga dapat dilihat dari sudut pandangan Sudut menyapu, Daripada melakukannya dari matlamat yang dilalui. Dalam kes ini terdapat perbincangan mengenai halaju sudut. Untuk pergerakan di lingkaran radio R, Terdapat hubungan antara arka (dalam radian) dan sudut:

S = r θ

Berhubung dengan kedua -dua belah pihak:

ds/dt = r (dθ/dt)

Memanggil terbitan θ berkenaan dengan t sebagai halaju sudut Dan menandakannya dengan huruf Yunani Ω "omega", anda mempunyai hubungan ini:

V = ΩR

Pecutan centripetal

Setiap pergerakan bulat mempunyai pecutan centripetal, yang selalu diarahkan ke pusat lilitan. Dia menjaga kelajuan berubah untuk bergerak dengan zarah kerana ia berubah.

Ia boleh melayani anda: lengkung penentukuran: Apa itu, bagaimana untuk melakukannya, contohnya

Pecutan centripetal ke_c Sama ada ke_R Ia selalu menunjuk ke pusat (lihat Rajah 2) dan berkaitan dengan halaju linear dengan cara ini:

ke_c = v² /R

Dan dengan halaju sudut seperti:

ke_c = (ΩR)² /R = Ω²R

Untuk pergerakan pekeliling seragam, kedudukannya S (t) Ia adalah bentuk:

S (t) = so+ vt

Di samping itu, pergerakan bulat yang bervariasi mesti mempunyai komponen pecutan yang dipanggil Pecutan tangen ke_T, yang berkaitan dengan mengubah magnitud kelajuan linear. Yeah ke_T  ia tetap, Kedudukannya ialah:

S (t) = s_{Sama ada} + v_{Sama ada}T + ½ a_Tt²

Dengan v_{Sama ada} Seperti kelajuan awal.

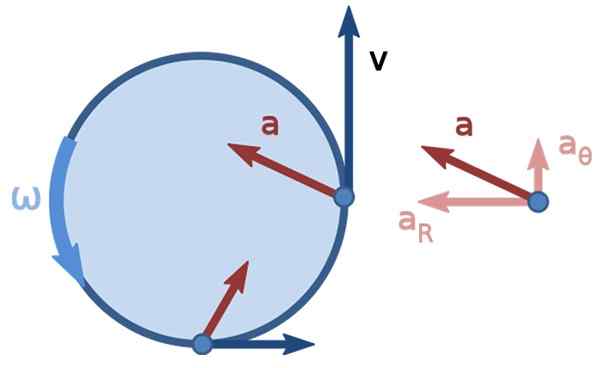Rajah 3. Pergerakan pekeliling yang tidak tidak digunakan. Sumber: nonuniform_circular_motion.PNG: Brews OHAREDORIVATIVATIVATIF Pekerjaan: Kooning Jons [CC BY-SA 3.0 (https: // creativeCommons.Org/lesen/by-sa/3.0)].

Latihan kelajuan linear yang diselesaikan

Latihan yang diselesaikan menyumbang untuk menjelaskan penggunaan konsep dan persamaan yang betul yang diberikan.

-Latihan diselesaikan 1 

Serangga bergerak pada separuh bulatan radius r = 2 m, bermula dari rehat pada titik sementara meningkatkan kelajuan linearnya, pada kadar p m/s². Cari: a) Selepas masa ia mencapai titik b, b) vektor halaju linear pada masa itu, c) pecutan vektor pada masa itu.

Rajah 4. Serangga bermula dari A dan mencapai B pada trajektori separuh bulatan. Ia mempunyai kelajuan linear. Sumber: Diri Diri.

Penyelesaian

a) Pernyataan menunjukkan bahawa pecutan tangen adalah malar dan bernilai π m/s², Maka sah untuk menggunakan persamaan untuk pergerakan seragam:

S (t) = s_{Sama ada} + v_{Sama ada}T + ½ a_T.t²

Dengan s_{Sama ada} = 0 dan V_{Sama ada} = 0:

S (t) = ½ a_T.t²

S = πR (Separuh panjang lilitan)

T = (2. πR /ke_T) ^½ S = (2π.2 /π)^½S = 2 s

b) v (t) = v_{Sama ada} + ke_T. T = 2π Cik

Apabila di titik B, titik vektor halaju linear dalam arah menegak ke arah (-dan):

Boleh melayani anda: apakah pemalar dielektrik?

v (t) = 2π Cik(-dan)

c) Percepatan tangen sudah ada, pecutan sentripetal hilang untuk mempunyai vektor kelajuan ke:

ke_c = v² / R = (2π)² / 2 m/ s² = 2π² Cik²

ke = a_c (-x) + a_T (-dan) = 2π²(-x)+ π (-dan) Cik²

-Latihan diselesaikan 2

Zarah bertukar dalam lingkaran radio 2.90 m. Pada masa tertentu pecutannya bernilai 1.05 m/s² dalam arah yang membentuk 32 dengan arah pergerakannya. Cari kelajuan linear anda di: a) Momen ini, b) 2 saat kemudian, dengan mengandaikan bahawa pecutan tangen adalah malar.

Penyelesaian

a) Direktorat pergerakan adalah tepat alamat tangen:

ke_T = 1.05 m/s² . cos 32º = 0.89 m/s² ; ke_C = 1.05 m/s² . Sen 32º = 0.56 m/s²

Kelajuan membersihkan ke_c = v² / R sebagai:

v = (r.ke_c)^1/2  = 1.27 m/s

b) Persamaan untuk pergerakan seragam adalah sah seperti berikut: V = V_{Sama ada} + ke_TT = 1.27 + 0.89 .2² m/s = 4.83 m/s

Rujukan

1. Bauer, w. 2011. Fizik untuk Kejuruteraan dan Sains. Jilid 1. MC Graw Hill. 84-88.
2. Figueroa, d. Siri Fizikal untuk Sains dan Kejuruteraan. Jilid 3. Edisi. Kinematik. 199-232.
3. Giancoli, d.  2006. Fizik: Prinsip dengan aplikasi. 6^th... Ed Prentice Hall. 62-64.
4. Gerakan relatif. Pulih dari: kursus.Lumenning.com
5. Wilson, J. 2011. Fizik 10. Pendidikan Pearson. 166-168.