Apakah hubungan antara kawasan rombus dan segi empat tepat?

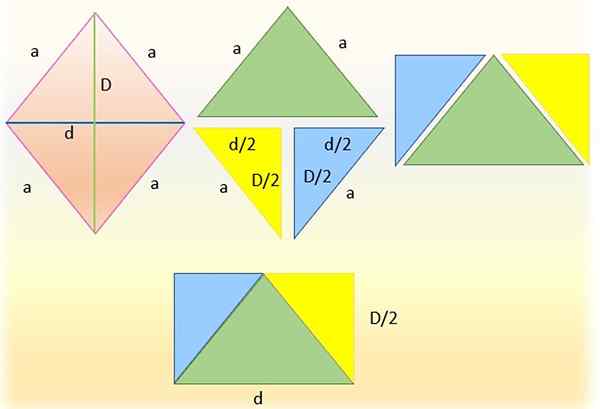
Mengurangkan rombus untuk mendapatkan segi empat tepat. Sumber: f. Zapata

Adalah mungkin untuk mengira kawasan rhombus (dan beberapa angka geometri lain) dari kawasan segitiga atau segi empat yang berkaitan, seperti paralelogram atau segi empat tepat.

Kawasan persegi panjang dan paralelogram adalah sama: ia dikira sebagai produk antara pangkal angka dan ketinggiannya berkenaan dengan pangkalan itu. Bagi bahagiannya, kawasan segitiga adalah separuh produk antara pangkalannya dan ketinggiannya.

Formula ini mudah diingat walaupun, secara semulajadi, geometri menawarkan formula eksklusif untuk kawasan rhombus, mengetahui ukuran pepenjuru utama dan kecilnya, dilambangkan sebagai D dan D, masing -masing:

Adalah mungkin untuk menyimpulkan ungkapan ini melalui urutan yang ditunjukkan dalam angka di atas.

Untuk melakukan ini, rombus di sebelah kiri dipotong oleh salah satu pepenjuru, yang dibuat dalam bahagian angka oleh pepenjuru kecil, sehingga memperoleh dua segitiga. Segitiga atas (hijau) dibiarkan dan yang lebih rendah dibahagikan kepada dua segitiga, memotong separuh daripada pepenjuru utama, memperoleh segi empat segi empat tepat yang sama biru dan kuning yang sama.

Kemudian hipotenus segitiga ini bertepatan dengan sisi segitiga hijau, kerana mereka mengukur yang sama, iaitu "a". Dan segi empat tepat akhirnya diperoleh, yang asasnya adalah "D" yang lebih rendah pepenjuru dan ketinggiannya adalah separuh daripada pepenjuru utama, iaitu: "D/2".

Kawasan segi empat tepat yang dibentuk bertepatan dengan tepat bahawa rombus, oleh itu ia dapat ditegaskan bahawa:

Boleh melayani anda: trinomial

Ke _berlian = (asas × ketinggian) _Rectangle = D × (D/2)

Hasilnya, seperti yang dapat dilihat, bertepatan dengan formula kawasan rhombus yang diberikan sebelumnya.

Kawasan rombo dan paralelogram

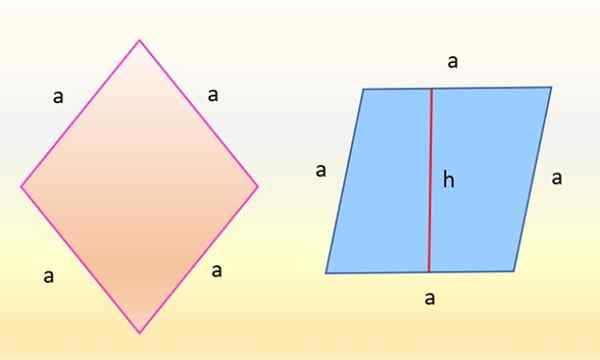
Kawasan Rhombus juga berkaitan dengan paralelogram, kerana kedua -dua angka geometri rata dan tergolong dalam keluarga kuadrilatural. Contohnya, dalam imej berikut terdapat rhombus di sebelah kiri dan selaras di sebelah kanan.

Kawasan rhombus di sebelah kiri adalah sama dengan paralelogram di sebelah kanan. Sumber: f. Zapata

Ternyata angka -angka itu sama, kerana apa yang telah berubah hanyalah orientasi. Rhombus di sebelah kiri, berwarna merah jambu, yang sisinya mempunyai ukuran yang sama: a, ia bertukar dengan cara yang salah satu sisinya benar -benar mendatar. Kemudian, rhombus mengambil bentuk paralelogram biru di sebelah kanan.

Dan kawasan selari ini juga merupakan produk antara asas "A" dan ketinggian berkenaan dengan pangkalan itu, yang dipanggil "H" dalam angka itu, oleh itu:

Ke _{Parallelogram} = A × h

Oleh kerana ia adalah angka yang sama, kawasan ini sama dan mengikutinya:

Ke _berlian = A × h

Oleh itu, mengetahui dan H dari paralelogram, kawasannya dikira dan ia akan bertepatan dengan rhombus.

Kawasan rombo tertulis dalam segi empat tepat

Hubungan lain antara rhombus dan segi empat tepat muncul apabila yang pertama didaftarkan di dalam kedua. Jika ini berlaku, simpang rombus bertepatan dengan titik tengah sisi segi empat tepat, yang dipaparkan di bawah:

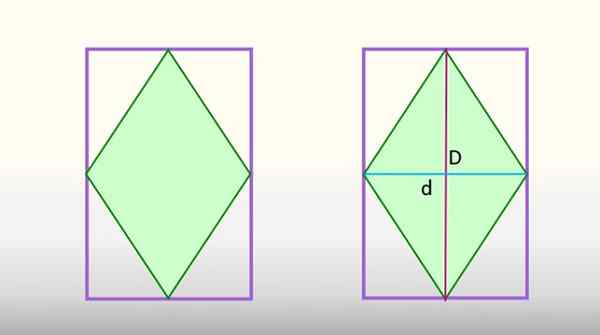Kawasan rhombus yang tertulis di segi empat tepat bersamaan dengan separuh kawasan segi empat tepat. Sumber: f. Zapata

Peruntukan ini menjadikan pepenjuru utama dan kecil dari rombus, angka itu dibahagikan kepada 8 segitiga yang sama, 4 yang sesuai dengan rombus, hijau, dan 4 yang lain adalah sebahagian dari segi empat tepat. Jika 4 segitiga terakhir ini bergabung bersama, mereka akan membentuk separuh segi empat tepat, dan 4 segitiga rhombus, yang lain.

Ia dapat melayani anda: segitiga isosceles

Oleh itu, kawasan rhombus bersamaan dengan separuh daripada kawasan segi empat tepat di mana ia didaftarkan, menyatakan bahawa:

Ke_berlian = A_Rectangle / 2

Ini mudah disahkan dengan mengira kawasan salah satu segitiga dan mengalikan dengan 4, kerana mereka sama. Kawasan segitiga mana -mana adalah separuh daripada produk antara asas dan ketinggiannya:

Ke _Segitiga = asas × ketinggian /2

Dari angka sebelumnya, diperhatikan bahawa asas salah satu segitiga adalah d/2 dan ketinggian adalah d/2, yang digantikan dalam formula sebelumnya memberikan:

Ke _Segitiga = (d /2) × (d /2) /2 = (d × d) /8

Mengalikan hasil ini dengan 4 untuk mempunyai kawasan Rhombus:

Ke _berlian = 4 (d × d) /8 = (d × d) /2

Bagi bahagiannya, separuh segi empat tepat adalah:

Ke _Rectangle / 2 = asas × ketinggian / 2

Sebagai asas segi empat tepat d dan ketinggiannya adalah d, ia tetap:

Ke_Rectangle / 2 = D × D/ 2

Yang tepatnya kawasan rombus berdaftar. Disimpulkan kemudian:

Kawasan rhombus yang didaftarkan dalam segi empat tepat bersamaan dengan separuh kawasan ini.

Latihan yang diselesaikan

Latihan 1

Berapa banyak kawasan rhombus yang langkah -langkah pepenjuru utama 14.6 cm dan pepenjuru yang lebih rendah 9.8 cm?

Penyelesaian

Dengan menggantikan d = 14.6 cm dan d = 9.8 cm di Formula Kawasan Rhombus:

Kawasan yang dicari adalah:

Ke _berlian = 14.6 cm × 9.8 cm = 143.1 cm²

Latihan 2

Dalam angka bahagian sebelumnya, pepenjuru utama rombus yang didaftarkan dalam langkah -langkah segi empat tepat d = 30 cm dan kawasan segi empat tepat bernilai 210 cm². Diminta untuk mengira:

a) Panjang pepenjuru kecil

Ia boleh melayani anda: segmen baris dan separuh

b) Kawasan rhombus, dalam dua cara: yang pertama melalui kawasan segi empat tepat dan yang kedua menggunakan formula kawasan rhombus. Periksa bahawa hasilnya sama.

Penyelesaian kepada

Kawasan segi empat tepat adalah produk antara pangkalannya dan ketinggiannya. Pepenjuru terbesar adalah ketinggiannya, sementara pepenjuru terkecil d akan menjadi pangkalan. Menggunakan formula kawasan dan menggantikan nilai pernyataan, anda mempunyai:

Ke _Rectangle = asas × ketinggian = d × 30 cm = 210 cm²

Maka pangkalannya bernilai:

D = 210 cm² / 30 cm = 7 cm

Penyelesaian b

Seperti yang dilihat di atas, kawasan rombus adalah separuh daripada kawasan segi empat tepat, dan ini diketahui:

Ke _berlian = 210 cm² /2 = 105 cm²

Hasilnya diperiksa dengan segera, menggantikan formula:

Diagonal sudah diketahui: d = 30 cm, d = 7 cm, kemudian:

Ke _berlian = 30 cm × 7 cm /2 = 105 cm²

Dibuktikan bahawa, seperti yang dijangkakan, kawasan rhombus adalah sama dalam kedua -dua kes.