Reaktansi induktif

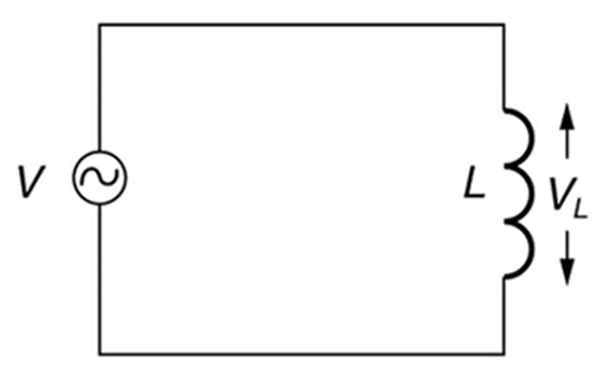
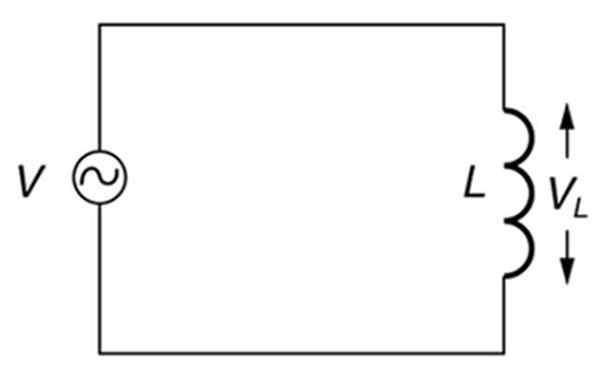Litar alternatif yang semata -mata induktif. Sumber: Buka Stax. Fizik kolej.

Apakah reaksi induktif?

The Reaktansi induktif Ia merujuk kepada pembangkang yang dibentangkan oleh gegelung ke laluan arus, dalam litar alternatif. Dengan kata lain, ia adalah keupayaan induk untuk mengurangkan arus dalam litar alternatif. Dilambangkan sebagai x_L, Nilainya bergantung kepada induktansi dan kekerapan sudut voltan:

X_L= Ω ∙ l

Di mana Ω adalah kekerapan sudut dalam induktansi radian/s dan l, diukur dalam henrios (h) dalam sistem unit antarabangsa jika.

Induktansi besar menghasilkan reaksi induktif yang hebat, kerana ketahanan mereka terhadap perubahan lebih besar. Dan reaktansi juga meningkat dengan kekerapan, jadi induktansi tertentu L akan menghasilkan reaksi yang lebih besar, semakin tinggi kekerapan voltan.

Unit Reaktan Induktif adalah Ohmio, yang dilambangkan oleh Ω. Ia adalah unit rintangan elektrik yang sama, tetapi tidak seperti ini, x_L Ia tidak tetap, kerana ia bergantung pada kekerapan voltan alternatif yang digunakan.

Oleh itu, dalam litar yang satu -satunya elemen adalah sumber alternatif dan induktansi (litar induktif), seperti yang ditunjukkan dalam angka di atas, reaksi induktif akan bergantung kepada kekerapan sumber.

Walau bagaimanapun, analogi X_L Dengan rintangan elektrik ia dapat diperluaskan ke litar induktif, yang membolehkan permohonan undang -undang ohm. Sekiranya x ditakrifkan_L sebagai nisbah antara amplitud voltan v_L Dalam induktor, dan semasa i_L yang melintasinya:

X_L = V_L / Yo_L

Anda boleh menulis undang -undang OHM untuk litar induktif semata -mata seperti berikut:

V_L = X_L∙ i_L

Formula reaksi induktif

Untuk mengira reaktansi induktif, formula yang diberikan pada mulanya digunakan, di mana l mewakili induktansi (henrios) dan Ω adalah kekerapan sudut (radian/kedua):

Boleh melayani anda: Eksperimen Millikan: Prosedur, Penjelasan, Kepentingan

X_L= Ω ∙ l

Adalah biasa untuk kekerapan yang dinyatakan dalam Hertz atau Hertzio (Hz). Dalam kes ini, ia dilambangkan oleh F dan berkaitan dengan kekerapan sudut melalui formula:

Ω = 2π ∙ f

Dalam kes ini, reaktansi dikira sebagai:

X_L= 2πf ∙ l

Dalam mana -mana formula ini, reaksi induktif menghasilkan ohm, seperti yang dijelaskan sebelumnya.

Kesan induktansi pada litar induktif

Kerana induktansi menentang perubahan atau variasi arus, reaktansi induktif dicirikan dengan melambatkan gelombang semasa berkenaan dengan gelombang voltan.

Dalam graf berikut, yang menunjukkan voltan v_L (Biru) dan semasa i_L (merah) Dalam induktor, kedua -duanya secara sinoid, diperhatikan bahawa kedua -dua gelombang sudah ketinggalan zaman 90º. Bermula pada t = 0, nilai voltan adalah maksimum, bagaimanapun, arus adalah sifar pada masa itu.

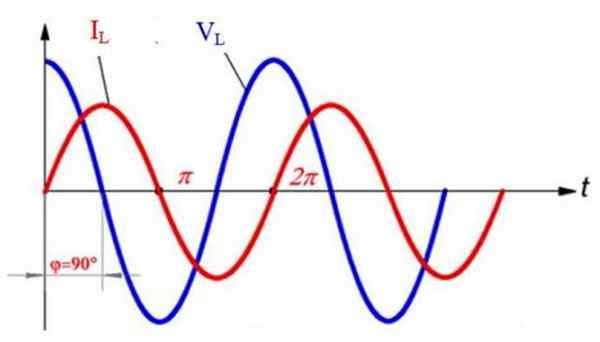Arus alternatif dan voltan dalam litar induktif. Disediakan oleh: f. Zapata.

Kemudian, diperhatikan bahawa arus mencapai nilai maksimumnya pada t = π /2, tetapi pada masa itu voltan dibatalkan dan melabur polaritasnya, iaitu, menjadi negatif. Pada masa yang sama, arus mengurangkan nilainya, sementara voltan menjadi semakin negatif.

Selanjutnya, pada t = π, voltan mencapai magnitud maksimumnya, walaupun dengan polaritas terbalik, dan kemudian arus dibatalkan. Dari semua ini, ia mengikuti bahawa setiap v_L Ia mencapai puncak, arus dibatalkan, dan setiap kali arus mencapai magnitud maksimumnya, voltan adalah 0.

Arus selalu mencapai puncaknya selepas voltan tidak, dan ini kerana, seperti yang dinyatakan pada mulanya, induktansi menentang kenaikan atau berkurangan.

Boleh melayani anda: Kelebihan mekanikal: formula, persamaan, pengiraan dan contoh

Cara mengira reaksi induktif

Mengira reaksi induktif sangat mudah: perlu mengetahui nilai induktansi dan kekerapan voltan alternatif yang digunakan. Kemudian, data ini diganti dalam salah satu formula yang diberikan dalam bahagian sebelumnya dan operasi yang sepadan dijalankan.

Contoh berikut dan latihan yang diselesaikan menunjukkan cara melakukannya dalam pelbagai situasi.

Contoh

Contoh 1

Katakan induktor l = 5 mh, yang mana voltan frekuensi alternatif digunakan 60.0 Hz. Reaktansi induktif dalam kes ini dikira oleh:

X_L= 2πf ∙ l

Tetapi sebelum menggantikan nilai, induktansi mesti menjadi Henrios, mendarabkan dengan faktor 1 × 10^-3. Oleh itu:

L = 5 × 10^-3 H

Jadi:

X_L= 2πf ∙ l = x_L= 2π × 60 Hz × 5 × 10^-3 H = 1. 88 ohm

Contoh 2

Sekarang induktansi yang sama disambungkan ke voltan frekuensi alternatif yang berbeza: 10.0 kHz. Dalam kes ini, induktansi memberikan reaksi yang lebih besar:

X_L= 2πf ∙ l = x_L= 2π × 10.0 × 10³ Hz × 5 × 10^-3 H = 314.2 ohm

Contoh 3

Voltan yang digunakan untuk induktansi contoh 1 dan 2 mempunyai nilai 120 V rms. Arus RMS masing -masing ditentukan melalui undang -undang ohm v_L = X_L∙ i_L:

Yo_L = V_L / X_L

Untuk kekerapan 60.0 Hz, arus adalah:

Yo_L = 120 v / 1. 88 ohm = 63.8 a

Dan untuk kekerapan 10.0 kHz:

Yo_L = 120 v / 314.2 ohm = 0.38 a

Oleh kerana dalam kes yang terakhir, reaksi jauh lebih besar, diharapkan arus akan lebih kecil. Harta ini menjadikan induktor penapis frekuensi tinggi, ciri yang digunakan untuk mengurangkan bunyi frekuensi tinggi dalam peralatan bunyi, atau untuk melindungi peranti dari UPS semasa secara tiba -tiba, antara aplikasi lain.

Boleh melayani anda: Steiner Theorem: Penjelasan, Aplikasi, Latihan

Latihan yang diselesaikan

Latihan 1

Tentukan reaksi induktif dalam litar yang terdiri daripada induktansi 2.5 mh, dalam siri dengan sumber voltan alternatif, yang kekerapannya adalah 75 r.p.m.

Penyelesaian

Revolusi atau kitaran lengkap sama dengan 2 radians, dan satu minit mempunyai 60 saat, oleh itu, kekerapan 75 r.p.M bersamaan dengan:

75 r.p.M = 75 × 2π radians / 60 saat = 7.85 radian/s

Dan dengan nilai ini, reaksi adalah:

X_L= Ω ∙ l = (7.85 radian/s) × 2.5 × 10^-3 H = 0.02 Ω

Latihan 2

Induktansi bersiri digunakan dengan sumber komputer untuk menapis bunyi dari frekuensi tinggi.

a) Apakah nilai induktansi minimum yang diperlukan untuk menghasilkan reaksi 2 kΩ, jika kekerapan isyarat yang ditapis adalah 15 kHz?

b) Cari reaksi induktor ini pada kekerapan 60 Hz.

Penyelesaian kepada

X_L = 2 kΩ = 2000 Ω

F = 15 kHz = 15000 Hz

Oleh itu, penjelasan persamaan x_L= 2πf ∙ l, anda ada:

L = x_L / 2π ∙ F = 2000 Ω / 2π × 15000 Hz = 0.0212 H = 21.2 mh

Penyelesaian b

Menggunakan x lagi_L= 2πf ∙ l, tetapi dengan f = 60 Hz, hasilnya:

X_L= 2π × 60 Hz × 0.0212 H = 8 ohm.

Rujukan

1. Bauer, w. (2011). Fizik untuk Kejuruteraan dan Sains. Jilid 1. MC Graw Hill. 
2. Giancoli, d. (2006). Fizik: Prinsip dengan aplikasi. 6th. Ed Prentice Hall.
3.  Katz, d. (2013). Fizik untuk saintis dan jurutera. Asas dan sambungan. Pembelajaran Cengage.
4. Buka Stax. Fizik kolej. Diperolehi dari: OpenStax.org.
5. Sears, z. (2016). Fizik universiti dengan fizik moden. Ke -14. Ed. Jilid 2. Pearson