Baris kedua

Kayu pintu taman ini bersedia sedemikian rupa sehingga mereka menentukan garis kering. Sumber: f. Zapata. Pxhere.com

Apakah garis kering?

Dalam pesawat, Baris kedua Mereka adalah orang -orang yang bersilang dan lengkung lain. Dalam kes dua baris, persimpangannya adalah titik, manakala garis secant pada lengkung, memotong ini dalam dua atau lebih mata.

Perhatikan pagar angka atas dengan teliti. Di atasnya telah ditarik beberapa warna lurus lurus, ditandakan sebagai l₁, L₂ dan l₃. Anak panah di kedua belah pihak bermaksud bahawa garis -garisnya berlanjutan selama -lamanya.

Nah, garis l₁, L₂ dan l₃ Mereka mengeringkan antara satu sama lain, kerana setiap pasangan mereka dipotong di mata ungu.

Di samping itu, garis l₁ dan l₂, Seperti l₁ dan l₃, Mereka menentukan 4 sudut antara satu sama lain, dua daripadanya akut dan bodoh yang lain, sementara garis l₂ dan l₃ Mereka berserenjang, yang bermaksud bahawa 4 sudut yang ditentukan oleh mereka adalah lurus.

Dua garisan selari tidak boleh kering, kerana, kerana keadaan mereka, mereka tidak mempunyai titik kebetulan. Sebaliknya, garis kebetulan tidak kering, kerana mereka mempunyai lebih dari satu titik yang sama.

Ciri -ciri garis pengeringan

• Dua garisan secant mempunyai titik yang unik sebagai persimpangan.
• Lereng dua garisan pengeringan mesti berbeza. Ya m₁ Ia adalah cerun garis l₁, dan m₂ Ia adalah cerun garis l₂, maka ia dipenuhi bahawa m₁ ≠ m₂.
• Lereng dua garisan pengeringan tegak lurus antara satu sama lain, yang lereng masing -masing adalah m₁ dan m₂, Mereka memenuhi hubungan m₁ = -1/ m₂. Di samping itu, produk skalar antara dua vektor v dan atau yang terkandung dalam baris ini adalah batal, kerana definisi produk skalar adalah v atau = v ∙ u ∙ cos θ, menjadi θ sudut antara vektor.
• Garis boleh menjadi secant ke lengkung atau angka geometri yang lain.
• Semasa bersilang, dua garisan pengeringan menjana 4 sudut, sama dua hingga dua atau sama antara satu sama lain.

Boleh melayani anda: persamaan pecahan

Bagaimana untuk mengetahui sama ada dua baris kering

Dari ciri -ciri garis pengeringan yang diterangkan di atas, adalah mungkin untuk menubuhkan tiga kriteria untuk mengetahui jika dua garisan kering:

-Membandingkan lereng. Sekiranya ini berbeza, garisan kering.

-Menjalankan produk skalar antara dua vektor yang terkandung dalam baris ini, yang dipanggil Pengarah. Sekiranya produk skalar tidak sah, garisan kering dan tegak lurus, dan jika ia bukan -zero, adalah mungkin untuk mengetahui sudut minimum di antara mereka, iaitu sudut akut yang ada di antara garis.

Dengan syarat bahawa sudut ini berbeza dari 0º, garis kering, dan jika ia sama dengan 0º, maka ia adalah garis selari.

-Secara langsung mengira sudut akut yang wujud di antara garis, mengenali lereng mereka. Ini boleh dilakukan melalui formula yang mengaitkan tangen sudut tersebut dengan lereng.

Biarkan m₁ dan m₂ lereng, dan θ sudut akut di antara mereka. Tangen θ diberikan oleh:

Jenis garisan pengeringan

Apabila dua baris mengeringkan satu sama lain, mereka boleh menjadi jenis berikut:

• Serong, Sekiranya apabila dipotong, mereka membentuk dua sudut akut dan dua sudut bodoh. Sudut ini adalah tambahan, iaitu, jumlah ukuran sudut ditambah dengan salah satu sudut bodoh adalah sama dengan 180º. Secara keseluruhan, jumlah 4 sudut adalah sama dengan 360º.
• Tegak lurus, Mereka yang bersilang 4 sudut bersamaan dengan 90º.

Cara mencari persimpangan antara dua baris

Sekiranya dua baris mengeringkan, mereka hanya mempunyai satu titik potong, yang menyelesaikan sistem dua persamaan linear dengan dua orang yang tidak diketahui. Jika garis diberikan secara umum: Ax + by = c, kata sistem persamaan adalah:

Boleh melayani anda: set tak terhingga: sifat, contoh

ke₁x + b₁ y = c₁

ke₂x + b₂ y = c₂

Bagaimana mencari persimpangan antara garis dan lengkung

Mengetahui persamaan kedua -dua garis dan lengkung, sistem persamaan dicadangkan dan, yang penyelesaiannya sesuai dengan titik persimpangan. Sekiranya sistem tidak mempunyai penyelesaian, garisan itu tidak bersangkutan dengan lengkung, dan tidak juga jika terdapat satu titik pemotongan, kerana, dalam hal ini, garis itu tangen ke lengkung.

Untuk garis pengeringan, seperti yang dinyatakan pada mulanya, sistem persamaan mesti mempunyai dua atau lebih penyelesaian.

Contoh garisan pengeringan

Pesawat Cartesian

Pesawat Cartesian ditentukan oleh dua baris, yang dipanggil X paksi dan Paksi y, mendatar dan menegak, masing -masing. Garis ini berserenjang dan titik persimpangan mereka dipanggil Asal sistem koordinat, atau hanya asal.

Pepenjuru poligon

Poligon adalah tokoh rata tiga atau lebih sisi, yang bergabung dengan titik yang disebut simpang. Segmen yang menyertai dua simpang bukan konsepsi adalah pepenjuru poligon, dan garis yang mengandungi segmen tersebut adalah secant ke poligon yang dipersoalkan.

Tali lilitan

Tali lilitan adalah segmen yang bergabung dengan dua mata. Tali utama adalah diameter, yang semestinya melalui pusat lilitan. Nah, garis yang mengandungi tali, termasuk diameter, adalah garis pengeringan ke lilitan.

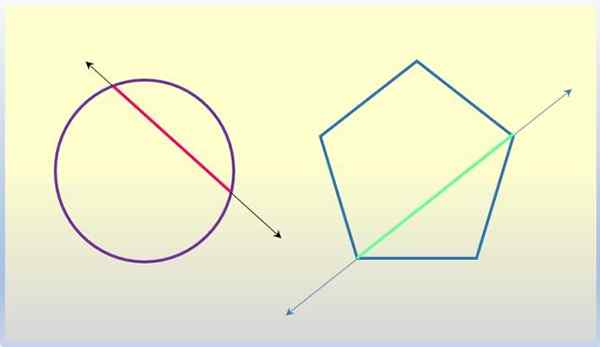Baris kedua ke angka geometri. Sumber: f. Zapata.

Kunci silang

Dengan alat ini kacang -kacangan yang memegang tayar ke roda kenderaan dilonggarkan. Garis bentuk lengan yang kering dan pada masa yang sama berserenjang.

Boleh melayani anda: variasi berkadar

Lirik Alphabet

Beberapa huruf abjad terdiri daripada strok lurus yang menentukan secant. Sebagai contoh, huruf x terdiri daripada dua pukulan yang dipotong bersama dalam satu titik dan huruf T terdiri daripada dua garis tegak lurus.

Latihan yang diselesaikan

Latihan 1

Tentukan sama ada garis yang diberikan oleh:

L₁ : y = 5x - 3

L₂ : y = -2x+1

Penyelesaian

Cerun garis yang diberikan dalam bentuk y = mx + b adalah nilai m, iaitu, pekali yang mengiringi x. Sejak m₁ = 5 dan m₂ = -2, yang berbeza, disimpulkan bahawa garis kering.

Latihan 2

Apakah sudut akut antara garis Latihan 1?

Penyelesaian

Nilai M diganti secara langsung₁ = 5 dan m₂ = -2 dalam formula yang diberikan dalam bahagian sebelumnya:

Oleh itu, sudut antara garis ialah θ = arctg 0.777 ... = 37.9º.

Latihan 3

Apakah persimpangan antara garis latihan sebelumnya?

Penyelesaian

Sistem persamaan dicadangkan seperti berikut:

Penyelesaiannya ialah: x = 4/7; y = -1/7 (boleh diselesaikan oleh mana -mana kaedah resolusi untuk sistem persamaan, atau dengan kalkulator).

Oleh itu, titik persimpangan garis adalah: p (4/7; -1/7).

Rujukan

1. Geometri Analitik.Maklumat. Baris kedua. Pulih dari: geometriaanalit.Maklumat.
2. Larson, r. 2006. Pengiraan dengan geometri analisis. Ke -8. Edisi. McGraw Hill.
3. Garis yang menyeberang. Pulih dari: Teacheraltuna.com.
4. Requena, b. Baris kedua. Pulih dari: universoformulas.com.
5. Villena, m. Geometri analisis di R3. Diperolehi dari: DSPACE.Espol.Edu.Ec.