Pengurangan istilah yang serupa

Apakah pengurangan istilah yang serupa?

The pengurangan istilah yang serupa Ini adalah kaedah yang digunakan untuk memudahkan ekspresi algebra. Dalam ungkapan algebra, istilah yang sama adalah yang mempunyai pembolehubah yang sama; iaitu, mereka mempunyai yang tidak diketahui yang sama yang diwakili oleh surat, dan mereka mempunyai eksponen yang sama.

Dalam sesetengah kes, polinomial adalah luas, dan untuk mencapai penyelesaian, anda mesti cuba mengurangkan ungkapan; Itu mungkin apabila terdapat istilah yang serupa, yang boleh digabungkan dengan menggunakan operasi dan sifat algebra seperti jumlah, penolakan, pendaraban dan pembahagian.

Penjelasan

Istilah yang sama dibentuk oleh pembolehubah yang sama dengan eksponen yang sama, dan dalam beberapa kes ini hanya berbeza dengan pekali berangka mereka.

Mereka yang tidak mempunyai pembolehubah juga dianggap istilah yang sama; iaitu istilah yang hanya mempunyai pemalar. Oleh itu, sebagai contoh, berikut adalah istilah yang sama:

• 6x² - 3x². Kedua -dua istilah mempunyai pembolehubah yang sama x².
• Ke -4²b³ + 2²b³. Kedua -dua istilah mempunyai pembolehubah yang sama untuk²b³.
• 7 - 6. Istilahnya tetap.

Istilah -istilah yang mempunyai pembolehubah yang sama, tetapi dengan eksponen yang berbeza dipanggil istilah yang tidak sama, seperti:

• Ke -9²B + 5AB. Pembolehubah mempunyai eksponen yang berbeza.
• 5x + dan. Pembolehubah berbeza.
• B - 8. Satu istilah mempunyai pemboleh ubah, yang lain adalah tetap.

Mengenal pasti istilah yang sama yang membentuk polinomial, ini dapat dikurangkan kepada satu, menggabungkan semua orang yang mempunyai pembolehubah yang sama dengan eksponen yang sama. Dengan cara ini, ungkapan itu dipermudahkan dengan mengurangkan bilangan istilah yang mengarangnya dan pengiraan penyelesaiannya difasilitasi.

Cara membuat pengurangan istilah yang serupa?

Pengurangan istilah yang serupa dilakukan dengan menggunakan harta bersekutu penambahan dan harta pengedaran produk. Menggunakan prosedur berikut, pengurangan istilah boleh dibuat:

• Pertama, istilah serupa dikumpulkan bersama.
• Koefisien (nombor yang mengiringi pembolehubah) dari istilah yang sama ditambah atau dikurangkan, dan sifat bersekutu, komutatif atau pengedaran digunakan, mengikut mana -mana yang mungkin berlaku.
• Kemudian istilah baru yang diperolehi ditulis, meletakkan di hadapan mereka tanda yang dihasilkan dari operasi.

Boleh melayani anda: Matematik diskret

Contoh

Kurangkan syarat ungkapan berikut: 10x + 3y + 4x + 5y.

Penyelesaian

Pertama, terma diperintahkan untuk mengumpulkan mereka yang serupa, menggunakan harta komutatif:

10x + 3y + 4x + 5y = 10x + 4x + 3y + 5y.

Kemudian harta pengedaran digunakan dan pekali yang mengiringi pembolehubah ditambah untuk mendapatkan pengurangan istilah:

10x + 4x + 3y + 5y

= (10 + 4) x + (3 + 5) dan

= 14x + 8y.

Untuk mengurangkan istilah yang sama, penting untuk mengambil kira tanda -tanda yang mempunyai pekali yang menemani pembolehubah. Terdapat tiga kes yang mungkin:

Pengurangan istilah yang serupa dengan tanda yang sama

Dalam kes ini, pekali ditambah dan di hadapan hasilnya tanda terma diletakkan. Oleh itu, jika mereka positif, istilah yang dihasilkan akan positif; Sekiranya terma negatif, hasilnya akan mempunyai tanda (-) disertai oleh pembolehubah. Sebagai contoh:

a) 22ab² + 12ab² = 34 AB².

b) -18x³ - 9x³ - 6 = -27x³ - 6.

Pengurangan istilah yang serupa cPada tanda yang berbeza

Dalam hal ini pekali dikurangkan, dan di hadapan hasil tanda pekali utama diletakkan. Sebagai contoh:

a) 15x²dan - 4x²dan + 6x²dan - 11x²dan

= (15x²dan + 6x²Y) + ( - 4x²dan - 11x²dan)

= 21x²Y + (-15x²dan)

= 21x²dan - 15x²dan

= 6x²dan.

b) -5A³B + 3 a³B - 4A³B + a³b

= (3 a³B + a³b) + (-5a³B - 4A³b)

= 4a³B - 9A³b

= -5 a³b.

Dengan cara ini, untuk mengurangkan istilah yang sama yang mempunyai tanda -tanda yang berbeza, istilah tambahan tunggal dibentuk dengan semua yang mempunyai tanda positif (+), pekali ditambah dan hasilnya disertai oleh pembolehubah.

Ia boleh melayani anda: lingkaran kesatuan: fungsi dan aplikasi trigonometri

Dengan cara yang sama, istilah subtractive terbentuk, dengan semua istilah yang mempunyai tanda negatif (-), pekali ditambah dan hasilnya disertai oleh pembolehubah.

Akhirnya, jumlah dua istilah yang dibentuk dikurangkan, dan tanda yang terbesar ditempatkan pada hasilnya.

Pengurangan istilah yang serupa dalam operasi

Pengurangan istilah yang sama adalah operasi algebra, yang boleh digunakan dalam jumlah, penolakan, pendaraban dan bahagian algebra.

Dalam jumlah

Apabila anda mempunyai beberapa polinomial dengan istilah yang sama, untuk mengurangkannya, syarat setiap polinomial diperintahkan menjaga tanda -tanda mereka, maka mereka ditulis selepas orang lain dan istilah yang serupa dikurangkan. Sebagai contoh, anda mempunyai polinomial berikut:

3x - 4xy + 7x²dan + 5xy².

- 6x²dan - 2xy + 9 xy² - 8x.

Dalam penolakan

Untuk menolak polinomial dari yang lain, Minuend ditulis dan kemudian menolaknya dengan tanda -tanda yang berubah, dan kemudian pengurangan istilah yang sama dibuat. Sebagai contoh:

5th³ - 3ab² + 3b²c

6ab² + 2³ - 8b²c

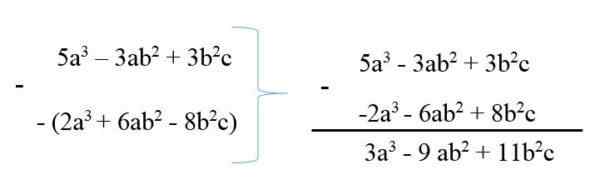
Oleh itu, polinomial diringkaskan pada 3A³ - 9ab² + 11b²c.

Dalam pendaraban

Dalam produk polinomial, istilah yang membentuk pendaraban untuk setiap istilah yang membentuk pengganda, memandangkan tanda -tanda pendaraban tetap sama jika ini positif jika mereka positif.

Mereka hanya akan berubah apabila mendarab dengan istilah yang negatif; Iaitu, apabila dua syarat tanda yang sama melipatgandakan hasilnya akan positif (+), dan apabila mereka mempunyai tanda yang berbeza hasilnya akan negatif (-).

Sebagai contoh:

a) (a + b) _* (A + b)

= a² + Ab + ab + b²

= a² + 2ab+ b².

b) (a + b) _* (A - b)

= a² - Ab + ab - b²

= a² - b².

teksi) _* (A - b)

= a² - AB - AB + B²

= a² - 2ab+ b².

Di bahagian

Apabila anda ingin mengurangkan dua polinomial melalui bahagian, polinomial ketiga mesti.

Ia boleh melayani anda: Ujian Tukey: Apa, dalam hal contoh, diselesaikan senaman

Untuk itu, terma dividen dan pembahagi mesti diperintahkan, dari kiri ke kanan, supaya pembolehubah dalam kedua -duanya berada dalam urutan yang sama.

Bahagian ini kemudiannya dilakukan, bermula dari tempoh pertama di sebelah kiri dividen antara yang pertama di sebelah kiri pembahagi, selalu mengambil kira tanda -tanda setiap istilah.

Contohnya, mengurangkan polinomial: 10x⁴ - 48x³dan + 51x²dan² + 4xy³ - 15y⁴ membahagikannya antara polinomial: -5x² + 4xy + 3y².

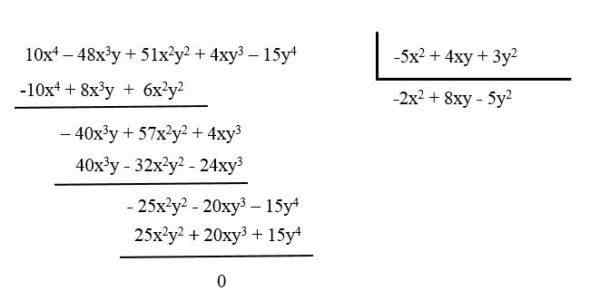
Polinomial yang dihasilkan adalah -2x² + 8xy - 5y².

Latihan yang diselesaikan

Latihan pertama

Kurangkan syarat ungkapan algebra yang diberikan:

15a² - 8ab + 6a² - 6ab - 9 +4a² - 13 ab.

Penyelesaian

Harta komutatif jumlahnya digunakan, mengelompokkan istilah yang mempunyai pembolehubah yang sama:

15a² - 8ab + 6a² - 6ab + 9 + 4a² - 13

= (15a² + 6th² + Ke -4²) + ( - 8ab - 6ab) + (9 - 13).

Kemudian harta pengedaran pendaraban digunakan:

15a² - 8ab + 6a² - 6ab + 9 + 4a² - 13

= (15 + 6 + 4) a² + ( - 8 - 6) AB + (9 - 13).

Akhirnya, mereka dipermudahkan dengan menambahkan dan menolak pekali setiap istilah:

15a² - 8ab + 6a² - 6ab + 9 + 4a² - 13

= 25a² - 14ab - 4.

Latihan kedua

Memudahkan produk polinomial berikut:

(8x³ + 7xy²)_*(8x³ - 7 xy²).

Penyelesaian

Setiap istilah polinomial pertama didarabkan oleh yang kedua, dengan mengambil kira bahawa tanda -tanda istilah adalah berbeza; Oleh itu, hasil pendarabannya akan negatif, serta undang -undang eksponen mesti digunakan.

(8x³ + 7xy²) _* (8x³ - 7xy²)

= 64 x⁶ - 56 x³_* Xy² + 56 x³_* Xy² - 49 x²dan⁴

= 64 x⁶ - 49 x²dan⁴.