Peraturan surat -menyurat fungsi

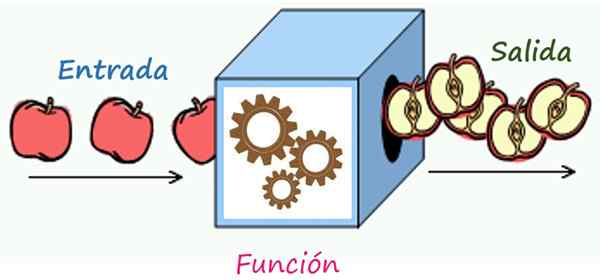
Peraturan surat -menyurat adalah mekanisme yang mengubah unsur -unsur kemasukan ke dalam elemen output. Sumber: Wikimedia Commons/F. Zapata

Apakah peraturan korespondensi fungsi?

The peraturan surat -menyurat fungsi Menunjukkan cara di mana unsur -unsur satu set berkaitan dengan unsur -unsur yang lain. Unsur -unsur set pertama dikenali sebagai domain, dan kepada yang kedua, seperti Codominium Sama ada kontradominium.

Hubungan atau hubungan antara set boleh ditentukan oleh arahan lisan atau bertulis, bagaimanapun, apabila set adalah berangka, peraturan surat -menyurat ditunjukkan oleh formula.

Formula ini mengandungi operasi yang mesti dilakukan dengan unsur -unsur perhimpunan permulaan, dan dengan itu memperoleh siri elemen yang termasuk dalam codominium.

Sekarang, apabila hubungan antara unsur -unsur adalah fungsi, peraturan surat -menyurat memenuhi dua syarat khas:

• Kepada setiap elemen domain dikaitkan, melalui peraturan surat -menyurat, satu elemen codominium, yang dikenali sebagai gambar.
• Imej ini unik, dengan kata lain, tiada elemen domain dikaitkan dengan lebih daripada satu elemen codominium.

Dengan cara ini, anda dapat membayangkan peraturan surat -menyurat fungsi sebagai mekanisme yang terkunci dalam kotak. Setiap nilai domain, tanpa pengecualian, boleh memasuki kotak dan keluar daripadanya diubah, melalui operasi yang ditunjukkan oleh peraturan surat -menyurat. Contohnya akan dilihat dengan segera.

Contoh

Contoh 1

Peraturan surat -menyurat fungsi dapat dinyatakan sebagai arahan bertulis, ketika unsur -unsur tidak berangka.

Sebagai contoh, terdapat satu set negara, dilambangkan sebagai p, dan satu lagi bandar C:

Ia boleh melayani anda: U -test of Mann - Whitney: Apa itu dan apabila diterapkan, pelaksanaan, contohnya

P = Kanada, Mexico, Sepanyol, Amerika Syarikat, Perancis, Argentina, Brazil, Jerman

C = Paris, London, Buenos Aires, Berlin, Mexico City, Ottawa, Río, New York, Madrid, Washington, Bern, Rom, Brasilia, Toronto

Menjadi peraturan surat -menyurat F Antara p dan c yang diberikan oleh:

F: P → c

Di mana F Ia adalah peraturan "... modal siapa .. ", Yang mengaitkan setiap negara di P (set permulaan), dengan ibu kota di C (set ketibaan).

Contohnya: "Sepanyol, yang modalnya Madrid ". Elemen "Sepanyol" tergolong dalam set pwart.

Perwakilan fungsi ini dapat dilakukan melalui gambarajah Venn atau hanya melalui pasangan yang diperintahkan.

Pasangan yang dipesan mengandungi, seperti namanya, dua elemen dengan perintah tertentu, dalam contoh ini, elemen pertama pasangan itu adalah negara, dan yang kedua, ibukota kota.

Bagi bahagiannya, gambarajah Venn adalah cara untuk memvisualisasikan fungsi, menunjukkan set permulaan dan ketibaan, serta peraturan surat -menyurat di antara mereka.

Perwakilan f seperti yang diperintahkan pasangan

F = (Kanada, Ottawa); (Mexico, Mexico City); (Sepanyol Madrid); (Amerika Syarikat; Washington); (Paris, Perancis); (Argentina Buenos Aires); (Brazil Brasilia); (Jerman, Berlin)

Pasangan pertama mengaitkan Kanada, yang modalnya Ottawa, rakan sekutu kedua Mexico, yang modalnya Mexico City dan sebagainya.

Perwakilan f sebagai gambarajah venn

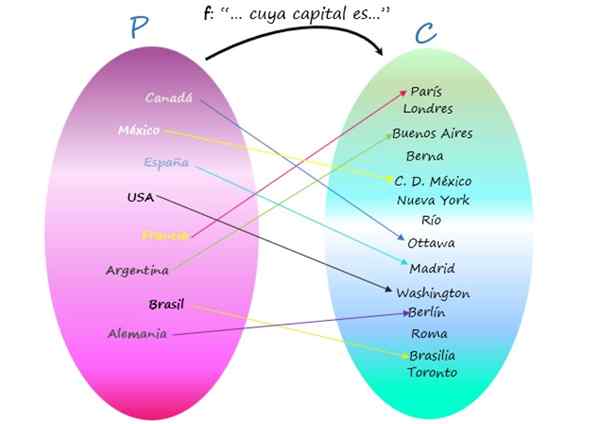
Perhatikan bahawa terdapat bandar -bandar yang bukan modal mana -mana negara, kerana, walaupun mereka adalah unsur -unsur codominium, mereka bukan imej mana -mana elemen set permulaan. Walaupun begitu, hubungan itu adalah fungsi, kerana yang penting ialah setiap negara mempunyai modal, dan ini unik.

Boleh melayani anda: kawasan pentagon biasa dan tidak teratur: bagaimana ia diambil, latihan

Subset yang dibentuk oleh unsur -unsur codominium yang merupakan imej beberapa elemen domain, dipanggil julat atau fungsi fungsi. Contohnya, laluan R dari F adalah:

R = Paris, Buenos Aires, Mexico City, Ottawa, Madrid, Berlin, Washington, Brasilia

Perlu ditanya sama ada hubungan antara c dan p dapat diwujudkan, di mana c menjadi set permulaan dan ketibaan. Jawapannya adalah ya, tetapi ia tidak akan menjadi fungsi, kerana terdapat bandar -bandar yang bukan modal, seperti New York, atau negara yang mereka modal tidak muncul di antara unsur -unsur kompleks P, seperti Rom.

Contoh 2

Apabila set berlepas dan set ketibaan adalah berangka, peraturan surat -menyurat fungsi yang menghubungkannya adalah formula. Sebagai contoh, jadilah penguasaan fungsi set berikut:

D = 0, 1, 2, 3, 4, 5, 6)

Peraturan surat -menyurat F: D → r yang menghubungkan unsur -unsur d dengan set nombor sebenar r ialah:

F: "Double"

Jika "x" adalah elemen set permulaan, f (x) adalah elemen yang sepadan dengan set ketibaan, dan peraturan surat -menyurat ditulis seperti ini:

f (x) = 2x

Codominium adalah set nombor sebenar. Subset reais adalah laluan fungsi ini, set nombor yang nilainya dua kali sebagai x:

R = 0, 2, 4, 6, 8, 10, 12

Dalam bentuk pasangan yang diperintahkan, peraturan surat -menyurat menghasilkan:

F = (0.0); (1.2); (2,4); (3,6); (4.8); (5.10); (6,12)

Pasangan yang dipesan boleh menjadi graf di pesawat Cartesian. Unsur pertama tork diletakkan pada paksi mendatar, juga dipanggil paksi abscissas atau paksi "x", manakala yang kedua pergi pada paksi menegak, paksi yang diperintahkan atau hanya paksi "y":

Boleh melayani anda: harta pengedaran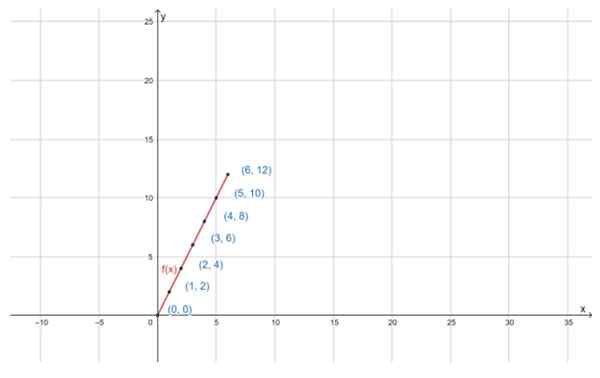 Grafik fungsi f (x) = 2x, untuk domain D yang ditentukan, adalah garis lurus. Sumber: f. Zapata melalui geogebra

Latihan

Tentukan peraturan surat -menyurat untuk hubungan berikut, menunjukkan sama ada fungsi mereka. Set nombor semulajadi adalah n dan yang sebenar adalah r.

Juga nyatakan domain, codominium dan laluan fungsi, dalam kes -kes di mana ia sepadan:

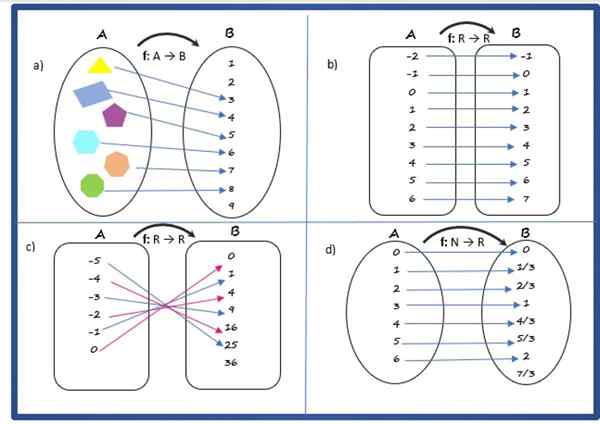
Penyelesaian kepada

Ia adalah fungsi, kerana setiap elemen set permulaan, yang terdiri daripada poligon, mempunyai imej yang unik dalam set ketibaan.

Peraturan surat -menyurat mengaitkan poligon dengan bilangan sisinya, domain terdiri daripada set A poligon:

A = segi tiga, kuadrilateral, pentagon, heksagon, heptagon, oktagon

Codominium adalah set nombor semulajadi pertama, termasuk 0.

B = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Dan co c adalah nombor semula jadi dari 3 hingga 8:

C = 3, 4, 5, 6, 7, 8

Penyelesaian b

Ia adalah fungsi, kerana ia memenuhi syarat -syarat yang dinyatakan di atas.

Peraturan surat -menyurat adalah:

f (x) = x + 1

Peraturan surat -menyurat menunjukkan bahawa fungsi itu ditakrifkan oleh r → r, oleh itu, domain adalah set nombor nyata. Dan co -oominium dan laluan juga bertepatan dengan sebenar.

Penyelesaian c

Ia adalah fungsi, dengan peraturan surat -menyurat:

f (x) = x²

Domain dan codominium adalah set reais, tetapi laluannya hanya terdiri daripada nombor sebenar positif, dilambangkan sebagai r r⁺ dan termasuk 0.

Penyelesaian d

Ia adalah fungsi. Peraturan surat -menyuratnya ialah:

f (x) = x/3

Domainnya adalah set nombor semulajadi N dan codominium, serta laluan, adalah nombor N sebenar r r.