Peraturan tuil

Apakah peraturan tuil?

The peraturan tuil Ini adalah prosedur matematik yang membolehkan untuk mengira pecahan, peratusan atau jumlah fasa yang terdapat dalam keseimbangan dalam sistem binari. Bukan sahaja matematik, tetapi juga cukup grafik dan tegas, sangat berguna dalam pengiraan fizikokimia dan kejuruteraan.

Peraturan ini terpakai kepada rajah fasa untuk sistem binari, tanpa mengira jenis sistem itu sendiri. Iaitu, fasa boleh menjadi pepejal, seperti dengan aloi; atau cecair dan gas, seperti yang kita lihat dalam sistem dalam keseimbangan cecair-wap.

Prinsip fizikal dan matematik tuil juga digunakan untuk tujuan kimia dan fizik bahan. Sumber: Jimbowley, CC BY-SA 3.0, melalui Wikimedia Commons

Peraturan tuil boleh digunakan secara langsung dengan mengambil kira nilai grafik dalam paksi abscissa, di mana pecahan global atau peratusan komponen yang paling tidak menentu biasanya akan berlaku, dalam hal cecair; atau refraktori, dalam hal logam dalam aloi mereka.

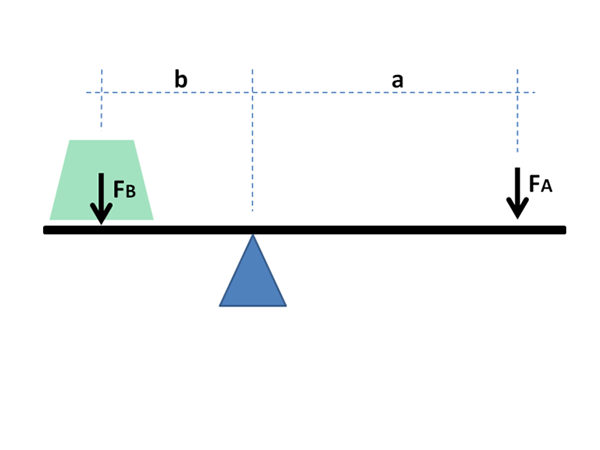
Seperti yang akan dilihat di bawah, namanya disebabkan oleh persamaan yang sangat besar dengan ungkapan matematik yang menunjukkan keseimbangan antara dua orang yang terletak di hujung rocker dengan Fulcro.

Lengan tuil mesti mengimbangi untuk mengimbangi massa beban; Dalam kes rajah fasa, pecahan dan tahi lalat fasa dalam keseimbangan bahan.

Penjelasan

Aspek grafik

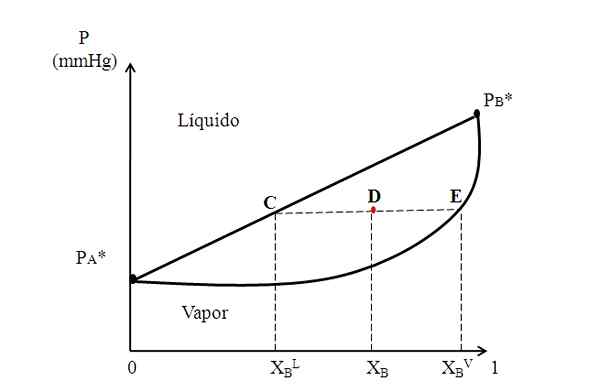Rajah binari hipotetikal di mana garis mengikat menunjukkan komposisi fasa cecair dan stim. Sumber: Gabriel Bolívar.

Di tengah -tengah rajah di atas kita mempunyai rantau di mana cecair dan stim wujud bersama; iaitu, rantau keseimbangan wap cecair. Di atas rantau ini, campuran A dan B akan menjadi cecair, dan di bawahnya akan menjadi soda kerana tekanan yang lebih rendah.

Sekarang, pertimbangkan campuran dengan komposisi x_B dan tekanannya meletakkannya pada titik d. Kami menarik dari titik D garis mendatar yang menyentuh garis dan lengkung di sisi, titik asal C dan E, masing -masing. Barisan ini, yang menyampaikan titik C, D dan E, C-d-E, adalah yang dikenali sebagai garis kesatuan, dan dengan memproyeksikannya ke arah paksi dan mesti memberi kita tekanan sistem.

Ia dapat melayani anda: Air Kealkalian: Apakah, penentuan dan kepentingan

Kemudian, dari titik -titik ini kita melukis garis lain berserenjang ke garis mengikat, yang akan memainkan paksi x. Sebagai titik E terletak pada lengkung stim, maka kita akan mempunyai pecahan molar b dalam fasa stim (x_B^V). Begitu juga, titik c, pada garis lurus cecair, akan memberi kita pecahan molar b dalam fasa cecair (x_B^L).

Peraturan tuil didasarkan tepat pada garis mengikat, dan jarak antara x_B^L, X_B dan x_B^V.

Potongan matematik

Pecahan molar global B adalah sama dengan:

X_B = n_B / (n^L + n^V)

Di mana n_B Mereka adalah jumlah tahi lalat B dalam fasa cecair dan stim, dan n^L dan n^V adalah tahi lalat masing -masing untuk fasa ini. Penjelasan n_B kita akan mempunyai:

n_B = X_Bn^L + X_Bn^V (1)

Sebaliknya, n_B Ia juga sama dengan:

n_B = n_B^L + n_B^V

= X_B^Ln^L + X_B^Vn^V  (2)

Sekarang menyamakan persamaan (1) dan (2) akan memberi kita:

X_Bn^L + X_Bn^V = X_B^Ln^L + X_B^Vn^V

Dan menyusun semula:

n^L(X_B - X_B^L) = n^V(X_B^V - X_B) (3)

n^L(C-d) = n^V(OF)

Kedua -dua ungkapan matematik terakhir ini adalah peraturan tuil. Perhatikan bahawa x_B - X_B^L Ia adalah jarak antara titik C dan D; dan x_B^V - X_B, Ia adalah jarak antara titik D-E: dua bahagian garis mengikat (lengan tuil).

Persamaan ini sangat serupa dengan yang menggambarkan keseimbangan massa pada rocker dengan Fulcro:

m₁L₁ = m₂L₂

Oleh itu, peraturan tuil akan membolehkan kita mengira jumlah tahi lalat n^L dan n^V dengan syarat bahawa jumlah tahi lalat campuran diketahui, n_T (n_T = n^L + n^V).

Borang kedua

Ekspresi sebelumnya untuk peraturan tuil berfungsi untuk mengira kuantiti (massa, tahi lalat, dll.) fasa dalam keseimbangan. Walau bagaimanapun, versi peraturan tuil yang paling terkenal membolehkan kita mengira pecahan atau peratusan setiap fasa, hanya mengambil jarak antara x_B, X_B^L dan x_B^V.

Pertimbangkan sistem yang sama di atas, mempunyai satu lagi bentuk peraturan tuil:

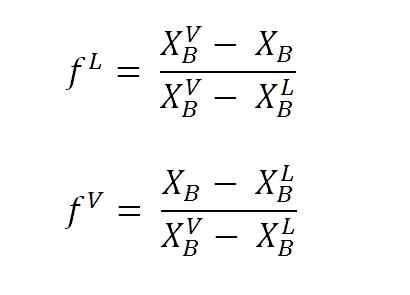Persamaan untuk mengira pecahan cecair dan stim menggunakan lengan tuil. Sumber: Gabriel Bolívar.

Di mana F ^L dan F ^VMereka adalah pecahan molar (atau peratusan, bergantung kepada graf) fasa cecair dan wap. Perhatikan bahawa, jelas, F ^L dan F ^V Mereka tidak mempunyai unit; manakala n^L dan n^V Ya, mereka mempunyai unit (tahi lalat, gram, dll.).

Boleh melayani anda: haba reaksi

Contoh

Kaedah 1

Dalam bekas 28 tahi lalat B dan 12 mol A bercampur. Tentukan jumlah dan pecahan molar untuk fasa yang terbentuk.

Kami mengira x_B:

X_B = (28 mol b)/ (28 mol b + 12 moles a)

= 0.7

Nilai ini sepadan dengan x_B daripada gambarajah teratas. Interceptions akan memberi kita kira -kira nilai berikut untuk x_B^L dan x_B^V:

X_B^L = 0.41

X_B^V = 0.94

Dengan peraturan tuil:

n^L(X_B - X_B^L) = n^V(X_B^V - X_B)

Dan mengetahui perkara itu n_T = n^L + n^V, Dan? n_T = 40 tahi lalat, maka kita jelaskan n^L Sama ada n^V Bergantung pada yang lain:

n^L(X_B - X_B^L) = (40 tahi lalat - n^L) (X_B^V - X_B)

Menyusun semula dan membersihkan n^L kita akan mempunyai:

n^L = (40 tahi lalat) (x_B^V - X_B) / (X_B^V - X_B^L)

Tidakkah ungkapan ini ingat bahawa F ^L? Sekarang menggantikan kita akan mempunyai:

n^L = (40 tahi lalat) (0.94 - 0.70) / (0.94 - 0.41)

= 18.11 tahi lalat dalam fasa cair

Kita boleh mengira n^V Dalam dua cara:

n^V = n^L(X_B - X_B^L) / (X_B^V - X_B)

Sama ada

n^V = 40 mol - 18.11 Moles

= 21.89 tahi lalat dalam fasa wap

Kaedah 2

Bagaimana jika kita mengira terlebih dahulu F ^L dan F ^V?

F ^L = (X_B^V - X_B) / (X_B^V - X_B^L)

= (0.94 - 0.70) / (0.94 - 0.41)

= 0.4528 atau 45.28%

Iaitu, 45.2% daripada tahi lalat berada dalam fasa cair, yang jumlahnya sama dengan:

n^L = F ^Ln_T

= (0.4528) (40 tahi lalat)

= 18.11 Moles

Dan F ^V Kita boleh mengira sama dengan dua cara:

F ^V = 1 - F ^L

Sama ada

F ^V = (X_B - X_B^L) / (X_B^V - X_B^L)

Menjadi nilainya:

F ^V = 0.5472 atau 54.72%

Dan oleh itu, n^V Ia akan sama dengan:

n^V = F ^Vn_T

= (0.5472) (40 tahi lalat)

= 21.89 Moles

Perhatikan bahawa menggunakan dua bentuk peraturan tuil sebagai kaedah pengiraan alternatif, hasil yang sama dapat dicapai. Kaedah 2 nampaknya lebih langsung dan mudah; Tetapi jika diperhatikan dengan teliti, setelah penjelasan diselesaikan n^L Sama ada n^V, Akan dilihat bahawa kedua -dua kaedah sebenarnya sama mudah.

Latihan yang diselesaikan

Seterusnya, dua latihan lain akan diselesaikan, di mana sekarang sistem yang dipertimbangkan akan melibatkan cecair-padat dan bukan cecair-wap. Juga, gambar rajah adalah grafik berkenaan dengan suhu sistem dan bukan tekanan mereka.

Latihan 1

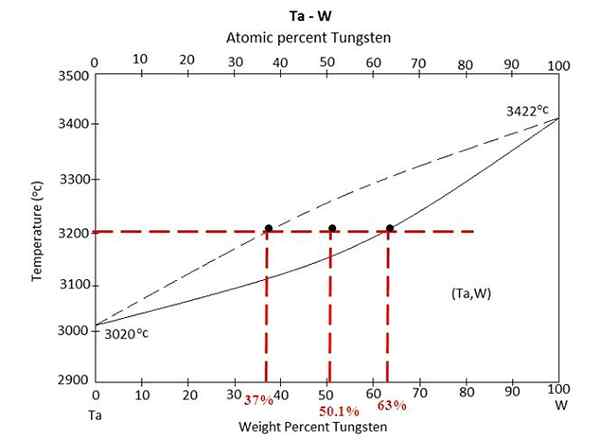Rajah fasa untuk aloi antara tantalo dan tungsten. Sumber: Bahanspedia, CC By-SA 4.0, melalui Wikimedia Commons

Kami mempunyai rajah fasa di atas aloi antara Tantalo dan Tungsten, TA-W. Pada paksi x peratusan jisim global tungsten, w% (m/m) diwakili.

Di dalam rantau keseimbangan cecair (TA+W) dan pepejal (aloi) terdapat campuran pada 3200 ºC. Tentukan massa setiap fasa dengan mengandaikan bahawa 100 gram aloi dipanaskan.

Ia boleh melayani anda: logam, bukan logam dan metalloid

Prosedur

Kali ini latihan akan diselesaikan menggunakan bentuk kedua peraturan tuil. Garis Kesatuan memberitahu kita bahawa: Dalam fasa pepejal kita mempunyai 63% tungsten, sementara dalam fasa cecair kita mempunyai 37% tungsten. Ini kerana tungsten cair ke suhu yang lebih tinggi (3422 ºC) daripada tantal (3020 ºC).

Jadi, kita ada:

W%^S atau w_S= 63%

W%^L atau w_L= 37%

Dan juga:

W₀ = 50.1%

Kami menggunakan peraturan tuil untuk F ^L:

F ^L = (63% - 50.1%) / (63% - 37%)

= 0.4961 atau 49.61%

Perhatikan bahawa jarak yang sepadan dengan fasa cecair adalah lengan tuil berhampiran fasa pepejal, seberang titik sederhana.

Oleh itu, jisim fasa cecair adalah:

(0.4961) (100 gram) = 49.61 gram cair

Dan fasa pepejal akan sama dengan:

100 gram - 49.61 gram = 50.39 gram aloi kaya dengan tungsten

Latihan 2

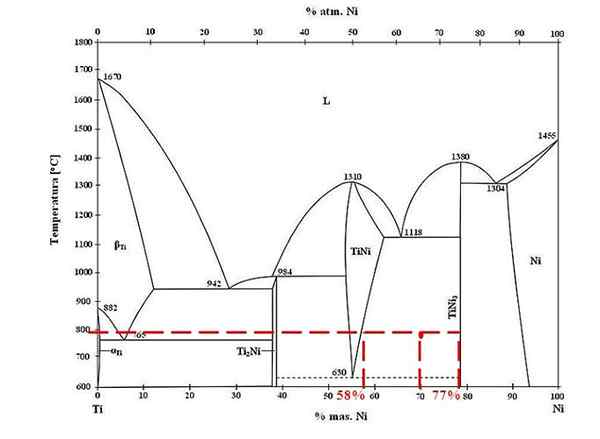Rajah fasa untuk aloi titanium-nikel. Sumber: Doomgiver, CC BY-SA 3.0, melalui Wikimedia Commons

Untuk aloi titanium dan nikel pada 800 ºC, dan dengan nikel 70%, tentukan berapa banyak tini dan tini₃ mereka hadir.

Prosedur

Kali ini mereka hanya meminta pecahan massa setiap fasa. Titik merah terletak di rantau keseimbangan antara fasa TINI dan TINI₃, Keluknya adalah di mana ia memainkan garis kesatuan yang mengalir ke nilai 58% atau untuk fasa TINI, dan 77% atau untuk fasa TINI₃.

Perhatikan bahawa titik merah lebih dekat dengan fasa tini₃ fasa tini. Ini bermaksud mesti ada lebih banyak tini₃ Tini itu; Dan oleh itu, jarak atau lengan tuil sepadan dengan tini₃ Ia mestilah yang paling lama, sebaliknya (70%-58%).

Mengetahui ini, kami terus mengira F ^Tini3:

F ^Tini3 = (70% - 58%) / (77% - 58%)

= 0.6316 atau 63.16%

Sesungguhnya, 63.16% daripada aloi sepadan dengan fasa tini₃. Sementara itu, fasa TINI sepadan dengan:

1 = F ^Tini3 + F ^Tini

F ^Tini = 1 - F ^Tini3

= 0.3684 atau 36.84%

Sebagai kesimpulan kepada latihan yang dibangkitkan, kita boleh mengatakan bahawa peraturan tuil sangat membantu untuk menentukan pecahan setiap fasa dalam keseimbangan untuk dua sistem komponen.

Rujukan

1. Walter J. Moore. (1963). Kimia Fizikal. Dalam kinetik kimia. Edisi keempat, Longmans.
2. Iran. Levine. (2009). Prinsip Fizikokimia. Edisi keenam. MC Graw Hill.
3. Wikipedia. (2020). Peraturan tuil. Diperoleh dari: dalam.Wikipedia.org
4. Michael Adewumi. (18 Mei 2020). Peraturan tuil. Pulih dari: eng.Libretxts.org
5. Adam Warren. (1997). Gambar rajah fasa: garis ikatan dan peraturan tuil. Pulih dari: Southampton.Ac.UK
6. Universiti Cambridge. (2020). Peraturan tuil. Diperolehi dari: doitpoms.Ac.UK