Peraturan Sarrus

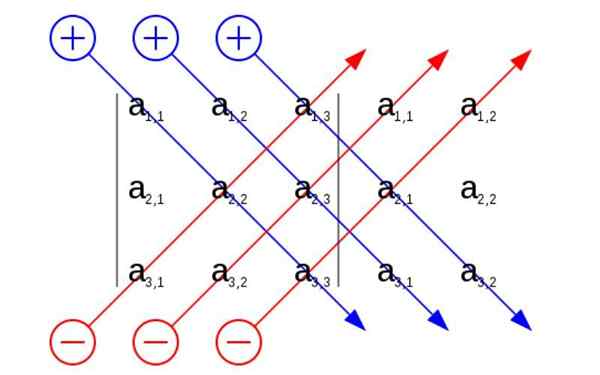
Peraturan Sarrus. Sumber: Pengguna: Sevela.P, cc by-sa 4.0, Wikimedia Commons

Apa itu peraturan Sarrus?

The Peraturan Sarrus Adalah teknik untuk mengira penentu matriks persegi 3 × 3 atau lebih besar. Sistem ini membolehkan penyelesaiannya lebih mudah. Ia juga digunakan untuk menentukan sama ada set vektor secara linear bebas dan membentuk asas ruang vektor.

Aplikasi ini berdasarkan kepada keterbatuhan matriks. Sekiranya matriks adalah biasa, penentunya berbeza dari 0. Sekiranya ia tunggal, penentunya bernilai 0. Penentu hanya boleh dikira dalam matriks persegi.

Untuk mengira matriks sebarang pesanan, teorem Laplace boleh digunakan. Teorem ini membolehkan kita memudahkan matriks dimensi tinggi, dalam jumlah penentu kecil yang kita hancurkan dari matriks utama.

Menyatakan bahawa penentu matriks adalah sama dengan jumlah produk setiap baris atau lajur, dengan penentu matriks yang dilampirkannya.

Ini mengurangkan penentu, sehingga penentu darjah n, menjadi penentu n-1. Sekiranya kita menggunakan peraturan ini dengan cara yang berturut -turut, kita dapat memperoleh penentu dimensi 2 (2 × 2) atau 3 (3 × 3), di mana pengiraannya lebih mudah.

Peraturan Sarrus

Pierre Frederic Sarrus (1798-1861) adalah ahli matematik Perancis. Kebanyakan perjanjian matematiknya berdasarkan kaedah penyelesaian persamaan dan pengiraan variasi, dalam persamaan berangka.

Dalam salah satu perjanjiannya, dia menyelesaikan salah satu daripada mekanik yang paling kompleks. Untuk menyelesaikan masalah kepingan yang diartikulasikan, Sarrus memperkenalkan transformasi pergerakan rectilinear alternatif, dalam pergerakan bulat seragam. Sistem baru ini dikenali sebagai mekanisme SARRUS.

Ia dapat melayani anda: eksternalisasi dan pengantarabangsaan kos

Penyelidikan yang paling banyak memberi dia adalah yang memperkenalkan kaedah baru untuk mengira penentu, dalam artikel "Kaedah Nouvelles mencurahkan la résolution des équations" ("Kaedah Baru untuk Resolusi Persamaan"), yang diterbitkan pada tahun 1833. Cara menyelesaikan persamaan linear ini dikenali sebagai Sarrus Rule.

Peraturan Sarrus membolehkan untuk mengira penentu matriks 3 × 3, tanpa menggunakan teorem Laplace, memperkenalkan kaedah yang lebih mudah dan lebih intuitif. 

Untuk dapat mengesahkan nilai peraturan Sarrus, kami mengambil matriks dimensi 3:

Pengiraan penentunya akan dibuat oleh produk pepenjuru utamanya, menolak produk dari pepenjuru songsang. Ini akan menjadi seperti berikut:

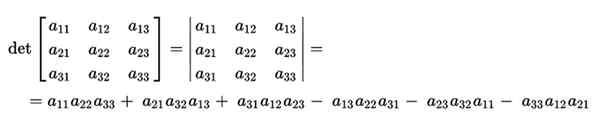
Peraturan Sarrus membolehkan kita mendapatkan visi yang lebih mudah apabila mengira pepenjuru penentu. Ia akan dipermudahkan dengan menambahkan dua lajur pertama ke belakang matriks.

Dengan cara ini, lebih jelas mengenai pepenjuru utamanya dan yang terbalik, untuk pengiraan produk.

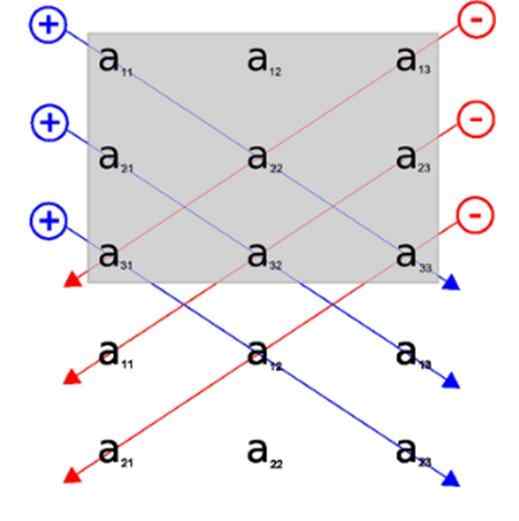
Melalui imej ini, kita dapat melihat permohonan peraturan Sarrus, kita memasukkan baris 1 dan 2, di bawah perwakilan grafik matriks awal. Dengan cara ini, pepenjuru utama adalah tiga pepenjuru yang muncul di tempat pertama.

Diagonal tiga songsang, pada gilirannya, adalah yang muncul pertama di belakang.

Dengan cara ini, pepenjuru muncul dengan cara yang lebih visual, tanpa merumitkan resolusi penentu, cuba mengetahui unsur -unsur matriks yang dimiliki oleh setiap pepenjuru.

Boleh melayani anda: kata -kata quechua diterjemahkan ke dalam bahasa Sepanyol

Seperti yang terdapat dalam imej, kami memilih pepenjuru dan mengira produk yang dihasilkan dari setiap fungsi. Pepenjuru yang muncul dalam warna biru adalah yang menambah. Kepada jumlah ini, kita tolak nilai pepenjuru yang muncul dengan warna merah.

Untuk mampatan menjadi lebih mudah, kita boleh menggunakan contoh berangka, bukannya menggunakan istilah algebra dan istilah subter.

Jika kita mengambil matriks 3 × 3, sebagai contoh:

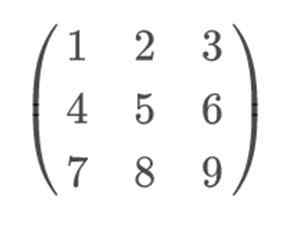
Untuk memohon peraturan Sarrus, dan menyelesaikannya dengan cara yang lebih visual, kita harus memasukkan baris 1 dan 2, sebagai baris 4 dan 5 masing -masing. Penting untuk mengekalkan baris 1 dalam kedudukan ke -4, dan baris 2 pada ke -5. Oleh kerana jika kita menukarnya, peraturan Sarrus tidak akan berkesan.

Untuk mengira penentu, matriks kami akan menjadi seperti berikut:

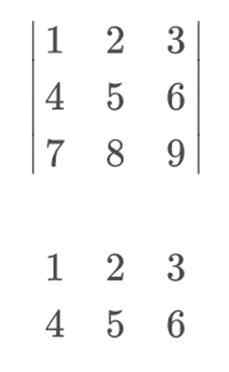
Untuk meneruskan pengiraan, kami akan melipatgandakan unsur -unsur pepenjuru utama. Descending yang mereka mulakan di sebelah kiri akan membawa tanda positif, sementara pepenjuru terbalik, yang merupakan yang bermula di sebelah kanan, membawa tanda negatif.

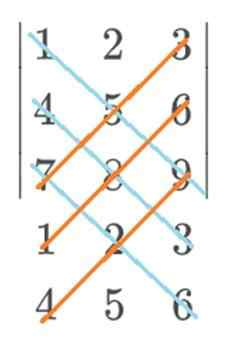
Dalam contoh ini, biru akan pergi dengan tanda positif dan merah dengan tanda negatif. Pengiraan akhir peraturan Sarrus akan tetap seperti ini:

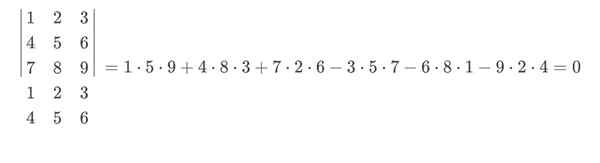
Lelaki penentu

Penentu dimensi 1

Sekiranya dimensi matriks adalah 1, matriks dengan cara ini: a = (a)

Oleh itu, penentunya akan menjadi seperti berikut: det (a) = | a | = a

Diringkaskan, penentu matriks A adalah sama dengan nilai mutlak matriks A, yang dalam kes ini adalah.

Dimensi penentu 2

Jika kita pergi ke matriks dimensi 2, kita memperoleh matriks jenis:

Boleh melayani anda: tauma

Di mana penentunya ditakrifkan sebagai:

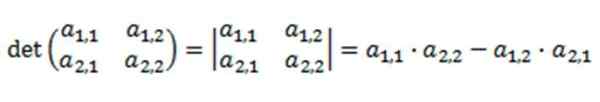
Resolusi penentu ini didasarkan pada pendaraban pepenjuru utamanya, mengurangkan produk pepenjuru songsangnya.

Penentu dimensi 3

Jika dimensi matriks adalah 3, matriks yang dihasilkan akan menjadi jenis ini:

Penentu matriks ini akan diselesaikan melalui peraturan Sarrus dengan cara ini:

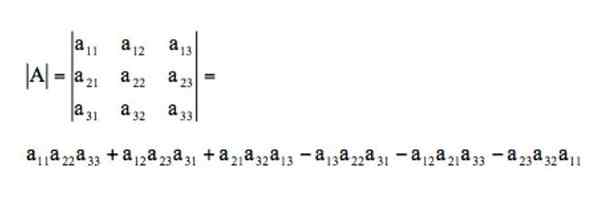
Rujukan

1. Anthony Nicolaides (1994). Penentu & Matriks. Lulus penerbitan.
2. M. Casteleiro Villalba (2004). Pengenalan kepada aljabar linear. Editorial ESIC.