Peraturan Sturges

Kami menerangkan apa peraturan Sturges, permohonannya dan memberi beberapa contoh

Apakah peraturan sturges?

The Peraturan Sturges Ini adalah kriteria yang digunakan untuk menentukan bilangan kelas atau selang yang diperlukan untuk menggambarkan satu set data statistik secara grafik. Peraturan ini dinyatakan pada tahun 1926 oleh ahli matematik Jerman Herbert Sturges.

Sturges mencadangkan kaedah mudah, berdasarkan bilangan sampel x yang dibenarkan untuk mencari bilangan kelas dan julatnya. Peraturan Sturges digunakan secara meluas di atas semua di kawasan statistik, khususnya untuk membina histogram frekuensi.

Penjelasan

Peraturan Sturges adalah kaedah empirikal yang digunakan secara meluas dalam statistik deskriptif untuk menentukan bilangan kelas yang mesti wujud dalam histogram frekuensi, untuk mengklasifikasikan satu set data yang mewakili sampel atau populasi.

Pada asasnya, peraturan ini menentukan lebar bekas grafik, histogram kekerapan.

Untuk menetapkan peraturannya Herbert Sturges menganggap gambarajah frekuensi yang ideal, yang terdiri daripada selang k, di mana selang I -ini mengandungi sejumlah sampel tertentu (i = 0, ... k - 1), diwakili sebagai:

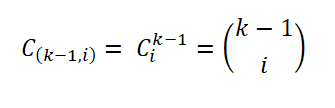
Bilangan sampel ini diberikan oleh bilangan cara di mana subset set boleh diekstrak; Iaitu, oleh pekali binomial, dinyatakan seperti berikut:

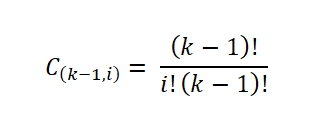Kemudian, sturges berkaitan bahawa histogram kekerapan akan menghampiri taburan normal apabila bilangan selang (k) meningkat mengikut teorem pusat had. Sedemikian rupa sehingga bilangan sampel setiap selang dapat dikira:

Ia boleh melayani anda: Enegon: Properties, Cara Membuat Enegon, Contoh

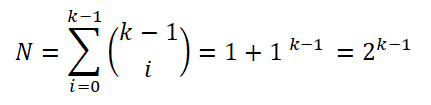
Untuk memudahkan ungkapan, dia menggunakan sifat logaritma di kedua -dua bahagian persamaan:

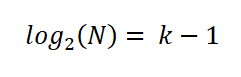
Oleh itu, sturges menegaskan bahawa bilangan selang k yang optimum diberikan oleh ungkapan:

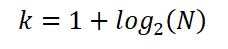
Ia juga boleh dinyatakan sebagai:

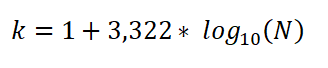
Dalam ungkapan ini:

• K adalah bilangan kelas.
• N ialah jumlah pemerhatian dalam sampel.
• Log adalah logaritma asas biasa 10.

Sebagai contoh, untuk menghuraikan histogram frekuensi yang menyatakan sampel rawak dari kedudukan 142 kanak -kanak, bilangan selang atau kelas yang akan dimiliki oleh pengedarannya ialah:

K = 1 + 3,322 _* log₁₀ (N)

K = 1+3,322_* Log (142)

K = 1+3,322_* 2,1523

K = 8.14 ≈ 8

Oleh itu, pengedaran akan berada dalam 8 selang.

Bilangan selang mesti selalu diwakili oleh nombor keseluruhan. Dalam kes di mana nilai adalah perpuluhan, penghampiran mesti dibuat kepada jumlah keseluruhan yang paling dekat.

Permohonan peraturan sturges

Peraturan Sturges digunakan terutamanya dalam statistik, kerana ia membolehkan pengagihan kekerapan melalui pengiraan bilangan kelas (k), serta panjang masing -masing, juga dikenali sebagai amplitud.

Amplitud adalah perbezaan dalam had atas dan bawah kelas, dibahagikan dengan bilangan kelas, dan dinyatakan:

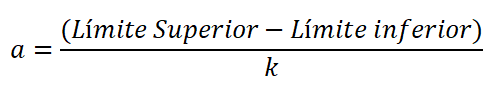
Terdapat banyak peraturan empirikal yang membenarkan pengedaran frekuensi. Walau bagaimanapun, peraturan Sturges biasanya digunakan kerana ia membuat penghampiran bilangan kelas, yang biasanya berlaku dari 5 hingga 15.

Dengan cara ini, ia menganggap nilai yang mewakili sampel atau populasi dengan betul; Iaitu, pendekatan tidak mewakili kumpulan yang melampau, dan tidak berfungsi dengan jumlah kelas yang berlebihan yang tidak membenarkan meringkaskan sampel.

Ia dapat melayani anda: sudut bertentangan dengan puncak (dengan senaman yang diselesaikan)

Contoh

Histogram frekuensi perlu dijalankan mengikut data yang diberikan, yang sesuai dengan usia yang diperolehi dalam tinjauan lelaki yang bersenam di gimnasium tempatan.

Untuk menentukan selang, saiz sampel atau bilangan pemerhatian harus diketahui; Dalam kes ini, terdapat 30.

Maka peraturan Sturges terpakai:

K = 1 + 3,322 _* log₁₀ (N)

K = 1+3,322_* Log (30)

K = 1+3,322_* 1,4771

K = 5.90 ≈ 6 selang.

Dari bilangan selang, anda boleh mengira amplitud yang akan mereka miliki; iaitu lebar setiap bar yang diwakili dalam histogram kekerapan:

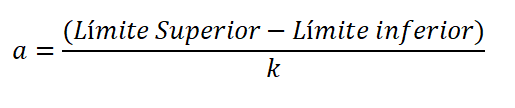
Had yang lebih rendah dianggap sebagai nilai data yang lebih rendah, dan bahagian atas adalah nilai tertinggi. Perbezaan antara had atas dan bawah dipanggil julat atau laluan pembolehubah (r).

Jadual mempunyai had atas adalah 46 dan lebih rendah 13; Dengan cara itu, amplitud setiap kelas akan:

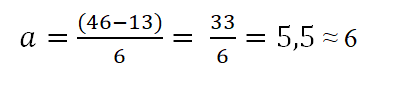
Selang akan terdiri daripada had atas dan bawah. Untuk menentukan selang -selang ini, ia bermula dengan mengira dari had yang lebih rendah, menambah ini amplitud yang ditentukan oleh peraturan (6), seperti berikut:

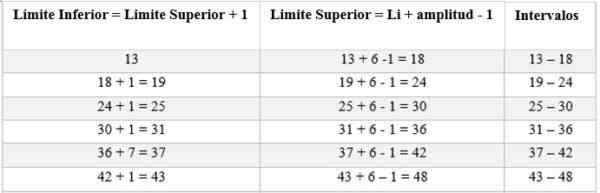
Maka kekerapan mutlak dikira untuk menentukan bilangan lelaki yang sesuai dengan setiap selang; Dalam kes ini ia adalah:

• Selang 1: 13 - 18 = 9
• Selang 2: 19 - 24 = 9
• Interval 3: 25 - 30 = 5
• Interval 4: 31 - 36 = 2
• Interval 5: 37 - 42 = 2
• Selang 6: 43 - 48 = 3

Dengan menambah kekerapan mutlak setiap kelas, ini mestilah sama dengan jumlah sampel; Dalam kes ini, 30.

Boleh melayani anda: homotecia negatif

Selanjutnya, kekerapan relatif setiap selang dikira, membahagikan kekerapan mutlak ini dengan jumlah pemerhatian:

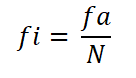
• Selang 1: Fi = 9 ÷ 30 = 0.30
• Selang 2: Fi = 9 ÷ 30 = 0.30
• Interval 3: Fi = 5 ÷ 30 = 0.1666
• Interval 4: Fi = 2 ÷ 30 = 0.0666
• Interval 5: Fi = 2 ÷ 30 = 0.0666
• Interval 4: Fi = 3 ÷ 30 = 0.10

Kemudian anda boleh membuat jadual yang mencerminkan data, dan juga rajah dari kekerapan relatif berhubung dengan selang yang diperoleh, seperti yang dapat dilihat dalam imej berikut:

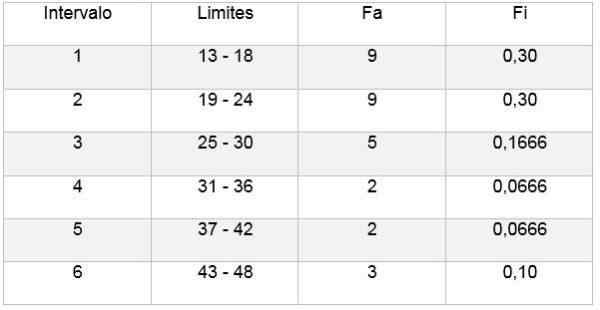
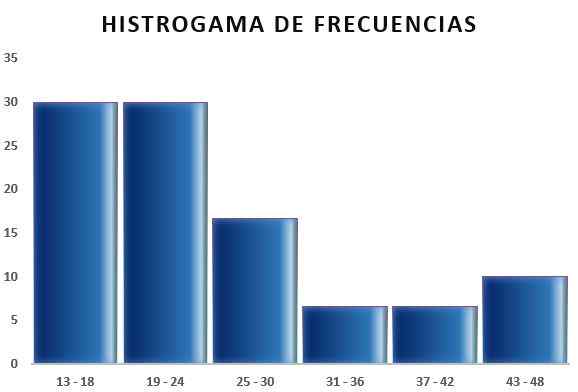
Dengan cara ini, peraturan Sturges membolehkan untuk menentukan bilangan kelas atau selang di mana sampel boleh dibahagikan, untuk meringkaskan sampel data melalui penjelasan jadual dan grafik.