Vektor Grafik Subs

The Penolakan vektor o Penolakan vektor antara vektor atau dan v dilambangkan oleh atau - v, Ia dikira dengan menambahkan vektor atau dengan vektor yang bertentangan v. Secara algebra penolakan dinyatakan seperti berikut:

atau - v = atau + (-v)

Adalah mungkin untuk menjalankan pengurangan vektor mengikut pelbagai prosedur, contohnya dalam bentuk grafik, dengan cara ini vektor v Ia ditarik oleh segmen garis berorientasikan -anak panah-.

Panjang anak panah sepadan dengan modul vektor, kecenderungan - mengenai garis rujukan yang diberikan - menunjukkan arah dan akhir menunjukkan arah vektor.

Vektor menentang v Ia mempunyai panjang dan arah yang sama, tetapi sebaliknya. Kemudian, sebelum penolakan antara atau dan v, Adalah perlu untuk menarik vektor yang bertentangan v, dan tambahkan vektor ini kepada anda.

Sangat penting untuk menekankan bahawa penolakan vektor tidak komutatif, iaitu, urutan vektor mengubah hasilnya, oleh itu:

atau - v ≠ v - atau

Prosedur grafik boleh dijalankan menggunakan mana -mana kaedah ini, yang langkahnya akan kita jelaskan di bawah:

-Kaedah Segitiga.

-Kaedah Parallelogram.

[TOC]

Kaedah sub -grafik grafik

Kaedah Segitiga

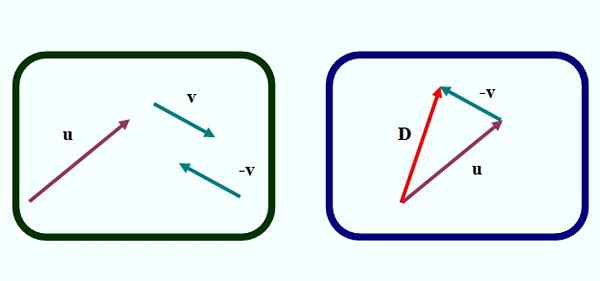
Rajah 1. Vektor Submance mengikut kaedah segitiga. Sumber: f. Zapata.

Dalam Rajah 1 kita mempunyai kaedah pertama untuk menolak dua vektor secara grafik. Ia mengenai Kaedah Segitiga, Kerana angka yang terbentuk ketika menubuhkan vektor adalah segitiga, seperti yang dapat kita lihat di sebelah kiri.

Untuk tolak atau - v Kami meneruskan seperti berikut:

-Lukis vektor -v Dari vektor v, dengan terjemahan dengan peraturan dan skuad, tetapi mengubah arah anak panah (imej kiri).

-Bergerak ke vektor -v sedemikian rupa yang asalnya bertepatan dengan akhir vektor atau (Imej yang betul).

Boleh melayani anda: geseran: jenis, pekali, pengiraan, latihan

-Vektor kemudian ditarik (merah dalam imej yang betul) yang berasal dari asal atau hingga akhir v. Panggilan D Dan ia adalah perbezaan vektor:

D = atau - v

Kaedah Parallelogram

Dalam kaedah paralelogram, vektor untuk menambah atau menolak mesti bertepatan dengan titik asal mereka. Katakan kita mahu mencari atau - v Dengan vektor kami yang ditunjukkan di atas, langkah -langkah untuk mencari penolakan vektor dengan kaedah ini adalah seperti berikut:

-Tentukan vektor yang bertentangan v, Apa itu -v, seperti yang diterangkan sebelum ini untuk kaedah segitiga.

-Ambil vektor dengan teliti atau dan -v sedemikian rupa sehingga asalnya bertepatan.

-Sekarang garis selari yang dibahagikan dari hujung setiap vektor. Angka yang terbentuk adalah selari dan dalam kes -kes khas di mana vektor berserenjang, ia adalah segi empat tepat atau persegi.

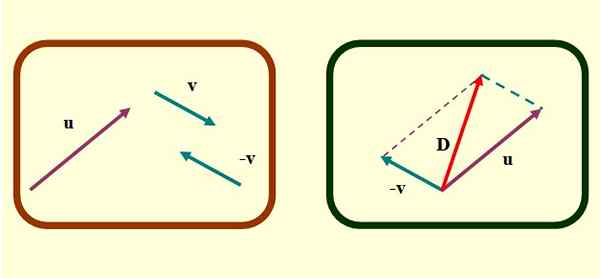Rajah 2. Kaedah parallelogram untuk pengurangan vektor. Sumber: f. Zapata.

-Akhirnya, vektor yang bermula dari asal umum atau dan v hingga akhir di mana garisan selari bersegmen diseberang. Ini adalah vektor D atau penolakan.

Penting

Cara lain untuk membuat penolakan adalah untuk menarik selaras seolah -olah anda ingin menambah vektor.

Tetapi bukannya melukis pepenjuru biasa jumlahnya, yang berasal dari asal -usul bersama ke persimpangan paralel, Diagonal bertentangan atau lebih pendek, Seperti yang dilihat dalam gambar:

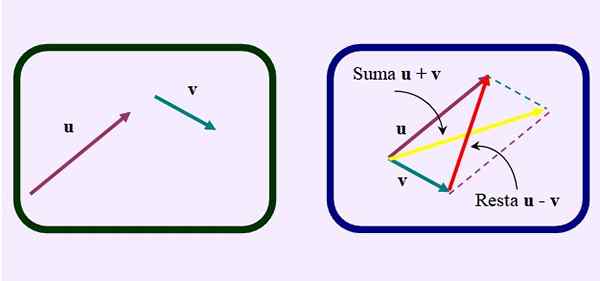Rajah 3. Cara lain untuk menjalankan pengurangan vektor melalui kaedah paralelogram. Sumber: f. Zapata.

Contoh penolakan vektor

- Contoh 1

Kapal menavigasi di sungai dan berbuat demikian ke arah yang bertentangan semasa. Pemerhati di tanah memerhatikan bahawa kelajuan kapal dikurangkan disebabkan oleh tindakan semasa.

Boleh melayani anda: bagaimana dengan tenaga yang terkandung dalam bahan?

Kelajuan adalah vektor dan dalam contoh ini, kelajuan titik kapal dalam satu arah dan arus mempunyai arah yang sama dan arah yang bertentangan. Kelajuan bersih kapal adalah jumlah kedua -dua vektor.

Contohnya, jika instrumen kapal. Sebagai v = v ' +vc, iaitu vc kelajuan arus yang dikira dengan pengurangan kelajuan v dan v' masing -masing: vc = v - v '= 30 km/h - 40 km/h = -10 km/ h.

- Contoh 2

Dalam sinematik kita mempunyai vektor penting yang menggambarkan perubahan:

-Anjakan untuk perubahan kedudukan.

-Kelajuan purata, untuk mengukur seberapa cepat kedudukannya berbeza dalam masa.

-Pecutan, untuk pengubahsuaian kelajuan sebagai fungsi masa.

Vektor anjakan

Vektor anjakan menerangkan perubahan kedudukan yang pengalaman tubuh dalam perjalanan pergerakannya.

Mari kita lihat contoh zarah yang menggambarkan trajektori rata yang ditunjukkan dalam angka, di mana ia pergi dari titik p₁ ke titik p₂.

Vektor yang diarahkan dari asal sistem koordinat x-y ke titik-titik ini adalah vektor kedudukan r₁ dan r₂, Manakala vektor anjakan adalah δr, mulai dari p₁ A p₂. Memang benar bahawa:

Δr = r₂ - r₁

Oleh itu, vektor anjakan adalah pengurangan antara vektor kedudukan akhir dan vektor kedudukan awal, seperti yang dinyatakan oleh angka berikut. Unitnya juga adalah kedudukan: meter, kaki, batu, sentimeter dan banyak lagi.

Boleh melayani anda: Perseus (Constellation): Lokasi, Mitologi dan Ciri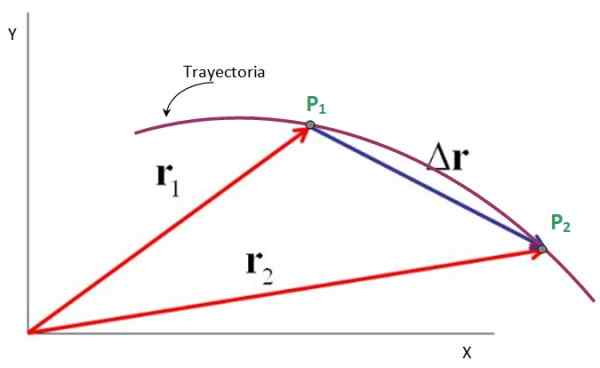Rajah 4. Vektor anjakan adalah perbezaan antara kedudukan akhir dan awal. Sumber: f. Zapata.

Purata kelajuan dan vektor pecutan purata

Bagi bahagiannya, vektor kelajuan purata v_m Ia ditakrifkan sebagai anjakan yang didarabkan oleh songsang selang masa:

 Dan pecutan purata adalah:

Latihan diselesaikan

Zarah yang menggambarkan bulatan mengambil 5 s untuk lulus dari titik a ke titik b. Dalam A mempunyai kelajuan v_Ke = 60 km/j ke arah paksi +x dan b adalah v_B = 60 km/j ke arah +dan. Tentukan purata pecutan dalam bentuk grafik dan analisis.

Penyelesaian

Dalam grafik, arah dan makna pecutan purata ditentukan oleh:

Dalam imej berikut adalah pengurangan v_B - v_Ke, melalui kaedah segitiga, kerana pecutan purata ke_m berkadar dengan δv. Segitiga yang terbentuk mempunyai dua kategori yang sama dan oleh itu sudut dalaman akut mengukur 45 º setiap satu.

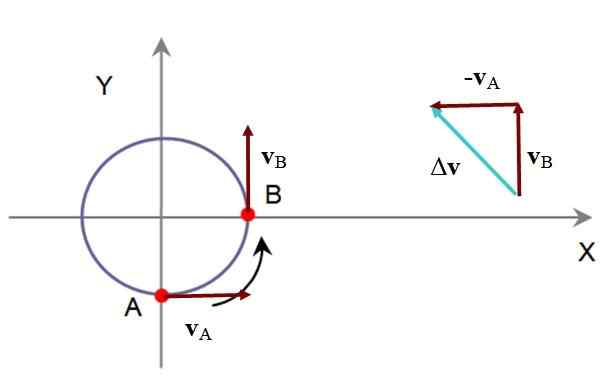Rajah 5. Rajah pergerakan zarah contoh yang diselesaikan. Sumber: f. Zapata.

Secara analitik, jika alamat +x bertepatan dengan vektor unit Yo dan alamat +dan dengan vektor unit J, Jadi:

Δv = 60 km/j J - 60 km/j Yo

Mengambil Δt = 5 s, mengikut maklumat pernyataan, pecutan purata adalah:

ke_m = (60 km/j J - 60 km/j Yo) / 5 s = 12 (J-Yo) Km/(h.s)

Rujukan

1. Bauer, w. 2011. Fizik untuk Kejuruteraan dan Sains. Jilid 1. MC Graw Hill.
2. Bedford, 2000. Ke. Mekanik untuk Kejuruteraan: Statik. Addison Wesley.
3. Figueroa, d. (2005). Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 1. Kinematik. Diedit oleh Douglas Figueroa (USB).
4. GiMbattista, a. 2010. Fizik. 2. Ed. McGraw Hill.
5. Sears, Zemansky. 2016. Fizik universiti dengan fizik moden. Ke -14. Ed. Jilid 1.
6. Tipler, ms. 2006. Fizik untuk Sains dan Teknologi. Edisi ke -5. Jilid 1. Editorial kembali.